反比例函数教案

反比例函数教案

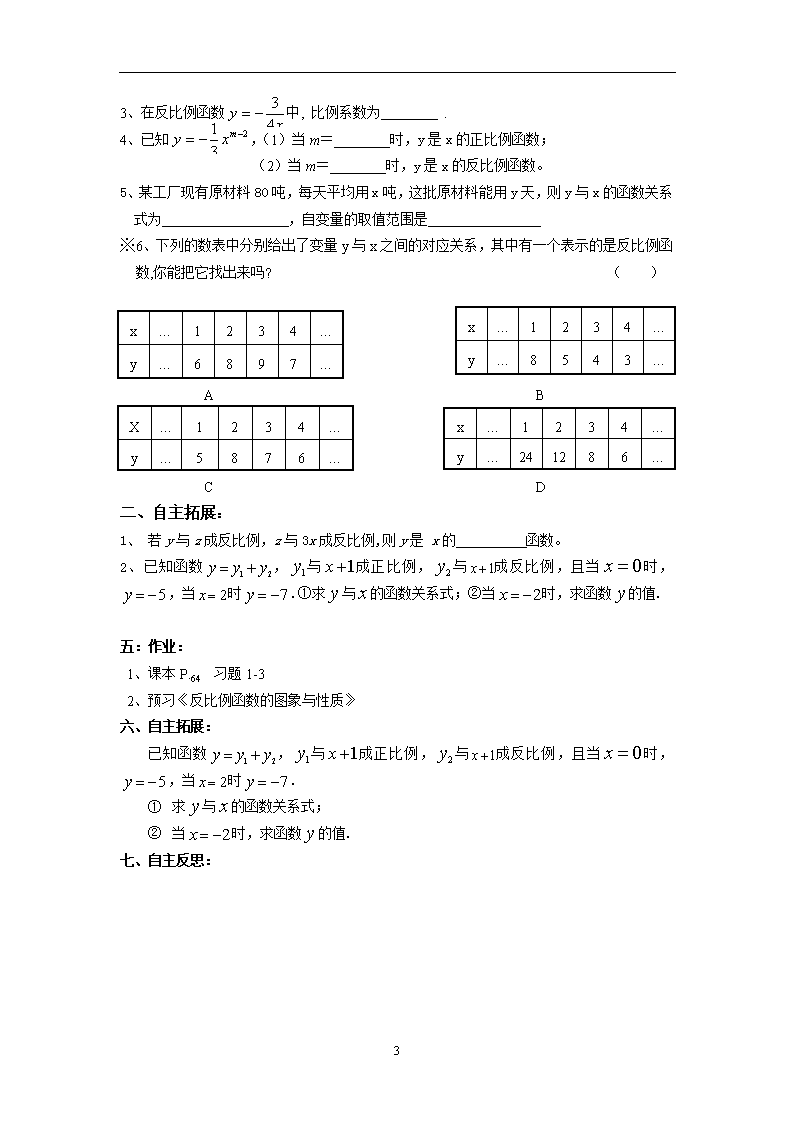
‎11．1反比例函数 教学目标： ‎ ‎1、理解反比例函数的概念。‎ ‎2、能根据实际问题中的条件确定反比例函数的解析式。‎ ‎3、能判断一个给定函数是否为反比例函数。‎ 教学重点：反比例函数的概念。‎ 教学难点：理解并掌握反比例函数的概念。‎ 教学过程：‎ 引入：‎ 汽车从江阴出发开往睢宁（全程约为450km），全程所用的时间t(h)随速度v(km/h)的变化而变化.‎ ‎（1）你能用含有v的代数式表示t吗？ t= ‎ ‎（2）利用（1）中的关系式完成下表：‎ v/(km/h)‎ ‎60‎ ‎80‎ ‎90‎ ‎100‎ ‎120‎ t/h ‎ 随着速度的增大，全程所用的时间 ；反之，速度减小，时间 。‎ 即 ‎ ‎（3）速度t （填“是”或“不是”）时间v的函数吗？原因 ‎ 一、自主探究：‎ 用函数关系式表示下列问题中的两个变量之间的关系：‎ ‎1.一辆汽车从南京开往上海 ‎（1）若速度是60（km/h），那么行驶的路程s（km）随时间t（h）变化而变化； ‎ ‎（2）若路程约300km，全程所用时间t（h）随速度v（km/h）的变化而变化。 ‎ ‎2、一个面积为6400㎡的长方形的长a(m)随宽b(m)的变化而变化； ‎ ‎3、某银行为资助某社会福利厂，提供了20万元的无息贷款，该厂的平均年还款额y(万元)随还款年限x(年)的变化而变化； ‎ ‎4、游泳池的容积为5000m3，向池内注水，注满水所需时间t（h）随注水速度v（m3/h）的变化而变化； ‎ ‎5、实数m与n的积为－200，m随n的变化而变化； ‎ ‎6、现有80(g)水，平均每个瓶子的注水量y(g) 随瓶子数量x（个）的变化而变化； ‎ ‎7、一个正方体的表面积y(m2)随棱长x (m)的变化而变化。 ‎ 二、自主合作：‎ 3‎ 你能仿照正比例函数的定义，写出这种函数的定义吗？‎ 一般地，形如 （k为常数，k ）的函数叫做 ，其中 是自变量， 是 的函数,k是 .‎ 反比例函数中，自变量x的取值范围是 .‎ 请同学们把正比例函数和反比例函数进行比较，说说它们有哪些不同？‎ 反比例函数还可以表示成 的形式.‎ 三、自主展示：‎ 例1、下列关系式中的y是x反比例函数吗？如果是，比例系数k是多少？‎ ‎ ‎ 练习：填空（带※的为选做题）‎ ‎（1）函数是反比例函数，则a的取值范围是 ； ‎ ‎（2）若 为反比例函数,则m=_ _；‎ ‎（3）已知，（1）当m＝________时，y是x的正比例函数；‎ ‎（2）当m＝________时，y是x的反比例函数。‎ ‎※（4）函数是反比例函数，a= ，反比例函数的解析式为 ‎ 例2、一个面积为6400㎡的长方形的长a(m)随宽b(m)的变化而变化（长是大于宽的）。‎ ‎（1）a与b的函数关系式为 。‎ ‎（2）当a= 时，b=40; 当a =320时，b= 。‎ ‎(3)在这个问题中，自变量b的取值范围是 （ ）‎ ‎ A、b﹥80 B、0﹤b﹤80 C、b≥80 D、0﹤b≤80‎ 四、总结反思，共同提高 通过这节课的学习你有哪些收获?还有哪些问题?与同伴进行讨论。‎ ‎(如：你学到了什么?懂得了什么?你发现了什么?还有什么困惑?应注意什么?还想知道什么?)‎ ‎1.反比例函数的形式为： ；‎ 一、自主检测：（带※的为选做题）‎ ‎1、下列函数中，是的反比例函数的是 （ ）‎ A、 B、 C、 D、‎ ‎2、函数中,自变量的取值范围是 （ ）‎ A、 B、 C、 D、‎ 3‎ ‎3、在反比例函数中, 比例系数为 .‎ ‎4、已知，（1）当m＝________时，y是x的正比例函数；‎ ‎（2）当m＝________时，y是x的反比例函数。‎ ‎5、某工厂现有原材料80吨，每天平均用x吨，这批原材料能用y天，则y与x的函数关系式为 ，自变量的取值范围是 ‎ ‎※6、下列的数表中分别给出了变量y与x之间的对应关系，其中有一个表示的是反比例函数,你能把它找出来吗? （ ）‎ x ‎…‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎…‎ ‎6‎ ‎8‎ ‎9‎ ‎7‎ ‎…‎ x ‎…‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎…‎ ‎8‎ ‎5‎ ‎4‎ ‎3‎ ‎…‎ ‎ A B X ‎…‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎…‎ ‎5‎ ‎8‎ ‎7‎ ‎6‎ ‎…‎ x ‎…‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎…‎ ‎24‎ ‎12‎ ‎8‎ ‎6‎ ‎…‎ ‎ C D 二、自主拓展：‎ ‎1、 若y与z成反比例，z与3x成反比例,则y是 x的 函数。‎ ‎2、已知函数，与成正比例，与成反比例，且当时，，当时.①求与的函数关系式；②当时，求函数的值.‎ 五：作业：‎ ‎1、课本P.64 习题1-3‎ ‎2、预习《反比例函数的图象与性质》‎ 六、自主拓展：‎ 已知函数，与成正比例，与成反比例，且当时，，当时.‎ ① 求与的函数关系式；‎ ② 当时，求函数的值.‎ 七、自主反思：‎ 3‎