2020八年级数学上册第5章一次函数5

2020八年级数学上册第5章一次函数5

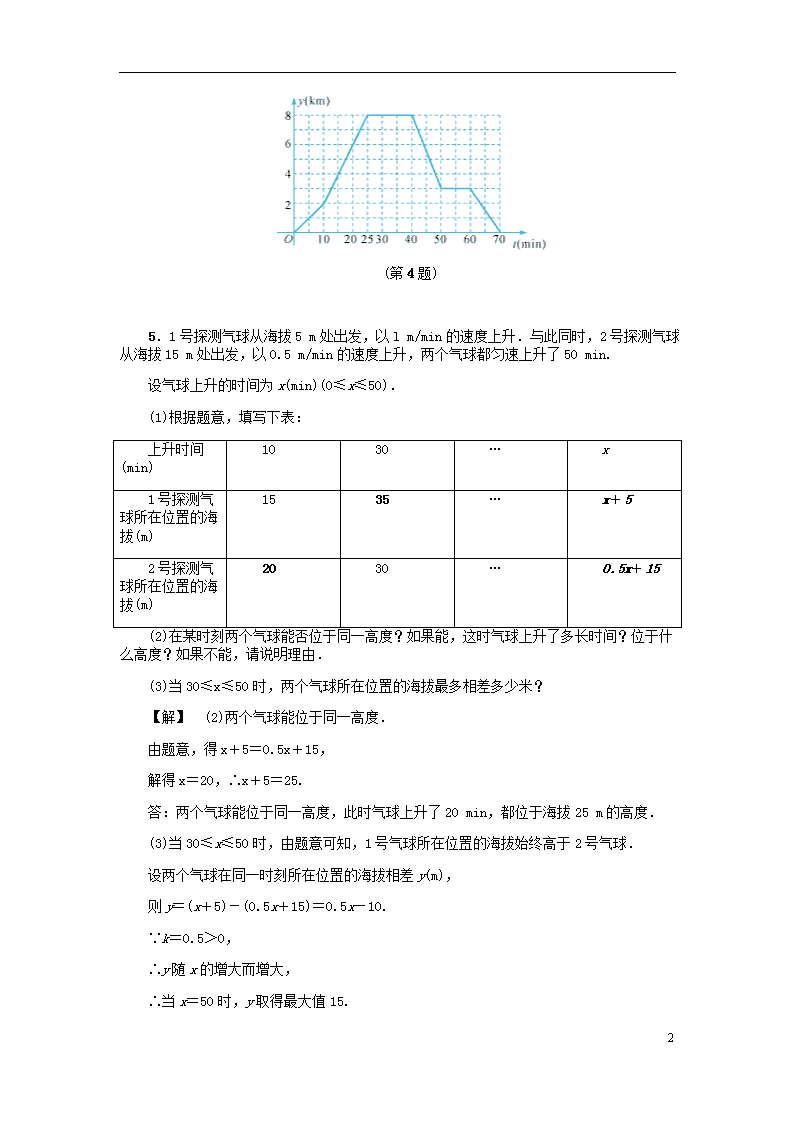
‎5.5 一次函数的简单应用(一) ‎ A组 ‎1．已知直线y＝ax＋b过点A(0，2)，B(－3，0)，则方程ax＋b＝0的解是(D)‎ A. x＝2 B. x＝0‎ C. x＝－1 D. x＝－3‎ ‎ (第2题)‎ ‎2．某社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该绿化组完成的绿化面积S(m2)与工作时间t(h)之间的函数关系如图，则该绿化组提高工作效率前每小时完成的绿化面积是(B)‎ A．‎300 m2‎ B．‎‎150 m2‎ C．‎330 m2‎ D．‎‎450 m2‎ ‎3．对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间存在着某种函数关系，从温度计上可以看出摄氏温度x(℃)与华氏温度y()有如下表所示的对应关系，则y与x之间的函数表达式是(B)‎ x(℃)‎ ‎…‎ ‎－10‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎…‎ y(°F)‎ ‎…‎ ‎14‎ ‎32‎ ‎50‎ ‎68‎ ‎86‎ ‎…‎ A. y＝x B. y＝1.8x＋32‎ C. y＝0.56x2＋7.4x＋32‎ D. y＝2.1x＋26‎ ‎4．一位自行车爱好者利用周末进行了一次骑车旅行，如图所示是这次旅行过程中自行车离出发地的距离y(km)与骑行时间t(min)之间的函数图象，观察图象，下列判断正确的是①③④(填序号)．‎ ‎①这次旅行的总路程为‎16 km；②这次旅行中用于骑车的总时间为60 min；③到达目的地之后休息了15 min；④如果返回途中不休息，可以提前10 min到达出发点．‎ 8‎ ‎(第4题)‎ ‎5．1号探测气球从海拔‎5 m处出发，以l m/min的速度上升．与此同时，2号探测气球从海拔‎15 m处出发，以‎0.5 m/min的速度上升，两个气球都匀速上升了50 min.‎ 设气球上升的时间为x(min)(0≤x≤50)．‎ ‎(1)根据题意，填写下表：‎ 上升时间(min)‎ ‎10‎ ‎30‎ ‎…‎ x ‎1号探测气球所在位置的海拔(m)‎ ‎15‎ ‎35‎ ‎…‎ x＋5‎ ‎2号探测气球所在位置的海拔(m)‎ ‎20‎ ‎30‎ ‎…‎ ‎0.5x＋15‎ ‎(2)在某时刻两个气球能否位于同一高度？如果能，这时气球上升了多长时间？位于什么高度？如果不能，请说明理由．‎ ‎(3)当30≤x≤50时，两个气球所在位置的海拔最多相差多少米？‎ ‎【解】　(2)两个气球能位于同一高度．‎ 由题意，得x＋5＝0.5x＋15，‎ 解得x＝20，∴x＋5＝25.‎ 答：两个气球能位于同一高度，此时气球上升了20 min，都位于海拔‎25 m的高度．‎ ‎(3)当30≤x≤50时，由题意可知，1号气球所在位置的海拔始终高于2号气球．‎ 设两个气球在同一时刻所在位置的海拔相差y(m)，‎ 则y＝(x＋5)－(0.5x＋15)＝0.5x－10.‎ ‎∵k＝0.5＞0，‎ ‎∴y随x的增大而增大，‎ ‎∴当x＝50时，y取得最大值15.‎ 8‎ 答：两个气球所在位置的海拔最多相差‎15 m.‎ ‎6．为迎接“五一”劳动节，某中学组织了甲、乙两个义务劳动小组，甲组x人，乙组y人，到“中华路”和“青年路”打扫卫生，根据打扫卫生的进度，学校随时调整两组人数．如果从甲组调50人去乙组，则乙组人数为甲组人数的2倍；如果从乙组调m人去甲组，则甲组人数为乙组人数的3倍．‎ ‎(1)求出x与m之间的函数表达式．‎ ‎(2)问：当m为何值时，甲组人数最少，最少是多少人？‎ ‎【解】　(1)由题意，得 整理，得 ‎①×3－②，得5x＝450＋‎4m，‎ ‎∴x＝m＋90.‎ ‎(2)∵x＝m＋90，∴x随m的增大而增大．‎ 又∵x，m，y均为正整数，‎ ‎∴当m＝5时，x取得最小值，最小值为×5＋90＝94，‎ 此时y＝2×94－150＝38，符合题意．‎ 答：当m＝5时，甲组人数最少，最少是94人．‎ B组 ‎7．8个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这8个正方形分成面积相等的两部分，则该直线l的函数表达式为(C)‎ ‎,(第7题))‎ A. y＝x B. y＝x C. y＝x D. y＝x 8‎ ‎【解】　设直线l与8个正方形最上面的交点为A，‎ 过点A作AB⊥y轴于点B，AC⊥x轴于点C.‎ ‎∵正方形的边长为1，∴OB＝3.‎ ‎∵经过原点的一条直线l将这8个正方形分成面积相等的两部分，‎ ‎∴易得S△ABO＝5，‎ ‎∴OB·AB＝5，∴AB＝，‎ ‎∴OC＝，∴点A.‎ 设直线l的函数表达式为y＝kx.‎ 将点A的坐标代入，得3＝k，‎ 解得k＝.‎ ‎∴直线l的函数表达式为y＝x.‎ ‎8．为更新果树品种，某果园计划新购进A，B两个品种的果树苗栽植培育．若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系．‎ ‎(第8题)‎ ‎(1)求y与x之间的函数表达式．‎ ‎(2)若购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．‎ ‎【解】　(1)当0≤x≤20时，设y与x之间的函数表达式为y＝k1x(k1≠0)．‎ 把点(20，160)的坐标代入，得20k1＝160.‎ 解得k1＝8，∴y＝8x.‎ 当x>20时， 设y与之间的函数表达式为y＝k2x＋b(k2≠0)．‎ 把(20，160)，(40，288)代入y＝k2x＋b，得解得 8‎ 则y＝6.4x＋32.‎ ‎∴y＝ ‎(2)由题意，得 解得22.5≤x≤35.‎ 设总费用为W元，则 W＝6.4x＋32＋7(45－x)＝－0.6x＋347.‎ ‎∵k＝－0.6<0，‎ ‎∴W随x的增大而减小，‎ ‎∴当x＝35，即购买B种苗35棵时，总费用最低，最低费用为－0.6×35＋347＝326(元)．‎ ‎(第9题)‎ ‎9．某农场急需氨肥8 t，在该农场南北方向分别有A，B两家化肥公司，A公司有氨肥3 t，每吨售价750元；B公司有氨肥7 t，每吨售价700元，汽车每千米的运输费用b(元/千米)与运输质量a(t)的关系如图所示．‎ ‎(1)根据图象求出b关于a的函数表达式，并写出自变量的取值范围．‎ ‎(2)若农场到B公司的路程是农场到A公司路程的2倍，农场到A公司的路程为m(km)，设农场从A公司购买x(t)氨肥，购买8 t氨肥的总费用为y元(总费用＝购买氨肥的费用＋运输费用)，求出y关于x的函数表达式(m为常数)，并向农场建议总费用最低的购买方案．‎ ‎【解】　(1)当0≤a≤4时，设b＝ka(k≠0)．‎ 把点(4，12)的坐标代入，得4k＝12，‎ 解得k＝3.‎ ‎∴b＝‎3a.‎ 当a≥4时，设b＝ma＋n(m≠0)．‎ 把点(4，12)，(8，32)的坐标分别代入，得 解得 8‎ ‎∴b＝‎5a－8.‎ ‎∴b＝ ‎(2)∵A公司有氨肥3 t，B公司有氨肥7 t，‎ ‎∴0≤x≤3，0≤8－x≤7，∴1≤x≤3，‎ ‎∴y＝750x＋3mx＋(8－x)×700＋[5(8－x)－8]×‎‎2m ‎＝(50－‎7m)x＋5600＋‎64m.‎ ‎∴当m＞时，到A公司买3 t，B公司买5 t费用最低；‎ 当m＝时，到A公司或B公司买费用一样；‎ 当m＜时，到A公司买1 t，B公司买7 t，费用最低．‎ 数学乐园 ‎10．【问题情境】用同样大小的黑色棋子按如图①所示的规律摆放，则第2018个图形中共有多少枚黑色棋子 ‎(第10题①)‎ 关于这个问题我们可以通过建立函数模型的方法求解．‎ ‎【建立模型】上述图形的规律我们可以借助建立函数模型探讨，具体步骤如下：‎ ‎(1)确定变量；(2)画函数图象；(3)求函数表达式；(4)代入验证．‎ ‎【解决问题】完成下列问题：‎ ‎(1)上述问题情境中以第x个图形为自变量，以第x个图形中黑色棋子的数量y为函数．‎ ‎(2)请在如图②所示的平面直角坐标系中画出图象．‎ ‎(3)猜想它是什么函数？求这个函数的表达式．‎ ‎(4)求第2018个图形中共有多少枚黑色棋子．‎ 8‎ ‎(第10题②)‎ ‎【解】　(2)如解图．‎ ‎(第10题解)‎ ‎(3)猜想它是一次函数．‎ 设猜想的一次函数表达式为y＝kx＋b，‎ 由题意，得解得 ‎∴y＝3x＋1.‎ 当x＝3时，y＝10；当x＝4时，y＝13.‎ 均符合所求的函数表达式y＝3x＋1.‎ ‎∴y＝3x＋1是所求的函数表达式．‎ ‎(4)当x＝2018时，y＝3×2018＋1＝6055.‎ 8‎ 答：第2018个图形中共有6055枚黑色棋子．‎ 8‎