八年级上数学课件《立方根》 (11)_苏科版

八年级上数学课件《立方根》 (11)_苏科版

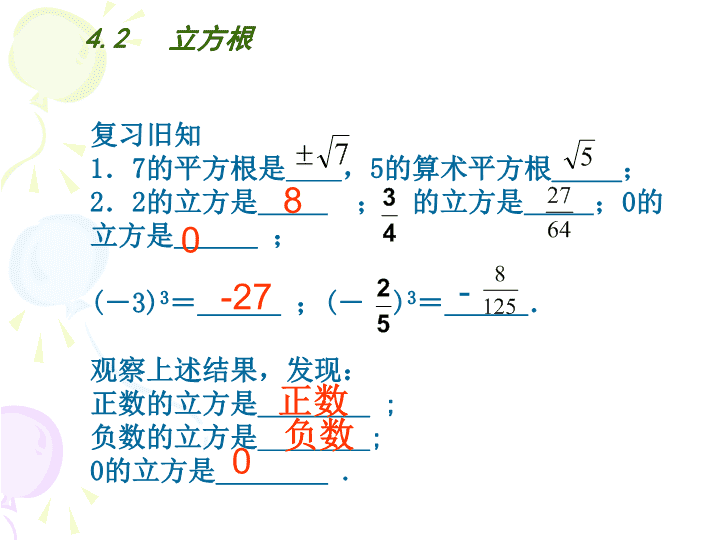
4.2　 立方根 复习旧知 1．7的平方根是 ，5的算术平方根_____； 2．2的立方是 ； 的立方是 ；0的 立方是 ； (－3)3＝ ；(－ )3＝ ． 观察上述结果，发现： 正数的立方是________ ; 负数的立方是________; 0的立方是________ . 4 3 5 2 7 5 8 64 27 0 -27 125 8- 正数 负数 0 1．现有一只体积为8cm3的正方体纸盒，它的每一条棱长 是多少？ （1）在这个实际问题中，提出了怎样的一个计算问题？ （2）你能得到一个数，使这个数的立方等于8吗？ （3）从这个问题中可以抽象得到一个什么数学概念？ 4.2　立方根 　　1．如果某种植物细胞可以近似看作是棱长为1的 正方体，那么当它的体积增大1倍时，这个正方体的 棱长是多少？ 11 1 x 4.2　立方根 2．做一个正方体纸盒，使它的容积为64cm3，正方 体纸盒的棱长是多少？如果要使正方体纸盒容积为 25cm3，它的棱长是多少？ 4.2　立方根 3 64 　　一般地，如果一个数的立方等于a，这个数就叫 做a的　　　　 ，也称为　　　　. 也就是说， 如果x3＝a，那么x叫做a的　　　 ，数a的立方 根记作 ，读作“三次根号a”. 例如：4的立方是64，所以4是64的立方根，记作　　 ＝4，又如，　是2的立方根，记作　　．　 　　 3 a 立方根 三次方根 立方根 3 2 3 2 由开平方定义得到：求一个数的立方 根的运算叫做开立方． 开立方和立方互为逆运算，因此求一个 数的立方根可以通过立方运算来求． 　　交流：下列各数有立方根吗？如果有，请写出 来；如果没有，请说明理由. , 0.001, 9,－3,－64, － ,0. 125 8 27 8 4.2　立方根 216 125 思考： 1.正数有立方根吗？负数呢？零呢？ 一个正数有一个正的立方根 0的立方根是0。 一个负数有一个负的立方根 立方根的性质: 平方根的性质与立方根的性质有何区别? 说一说： 总结： 立方根定义 1．立方根和平方根有何异同？ 2．立方根的性质及一个数的立方根的求法． 4.2　立方根 1.平方根、算术平方根 与立方根有何区别 ? 平方根 算术平方根 立方根 表示 方法 a的 取值 a为任意实数 性质 正数的平方 根有两个; 0的平方根 是0; 负数没有平 方根 正数的算术平方根是 正数; 0的算术平方根是0; 负数没有算术平方根 正数的立方根 是正数; 0的立方根是0; 负数的立方根 是负数 a a 3 a 0a 0a 例二: 求下列各式的值 )2()2()3(1 3 323 3 ）（ 3 33 33 33 1003212  ）（ 计算： ____;,643  xx 则若 .____,64 32  xx 则若 填空： =1 =-5050 2 ±2 例3 计算: 333 64)3(;64)2(;64)1(  结论: 通过前面的计算你能发现了什么? 1.互为相反数的两个数,它们的立方根 也是互为相反数 练一练:下列说法是否正确,并说明理由 1. 的立方根是 ; 2.负数不能开立方; 3.4的平方根是2； 4.互为相反数的数的立方根也是互为相反数; 5.立方根是它本身的数只有零; 6.平方根是它本身的数只有零; 7. 的立方根是4. 27 8 3 2 64 9.若一个数的平方根和立方根相同,则 这个数是_____;若一个数的立方根和 算术平方根相同则这个数是_____. 8.一个正方体的体积变为原来的64倍， 它的棱长变为原来的_____倍. 10.存在一个平方,立方,绝对值,倒数,算术 平方根,立方根都是它本身的数吗? 挑战自我 已知 求 的立方根. 0)27(64 233  ba bba )(  布置作业 1．立方根的定义与性质 2．如何求一个数的立方根（开立方） 3．立方根与平方根的区别