- 2021-11-01 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学上册第三章位置与坐标检测题新版北师大版
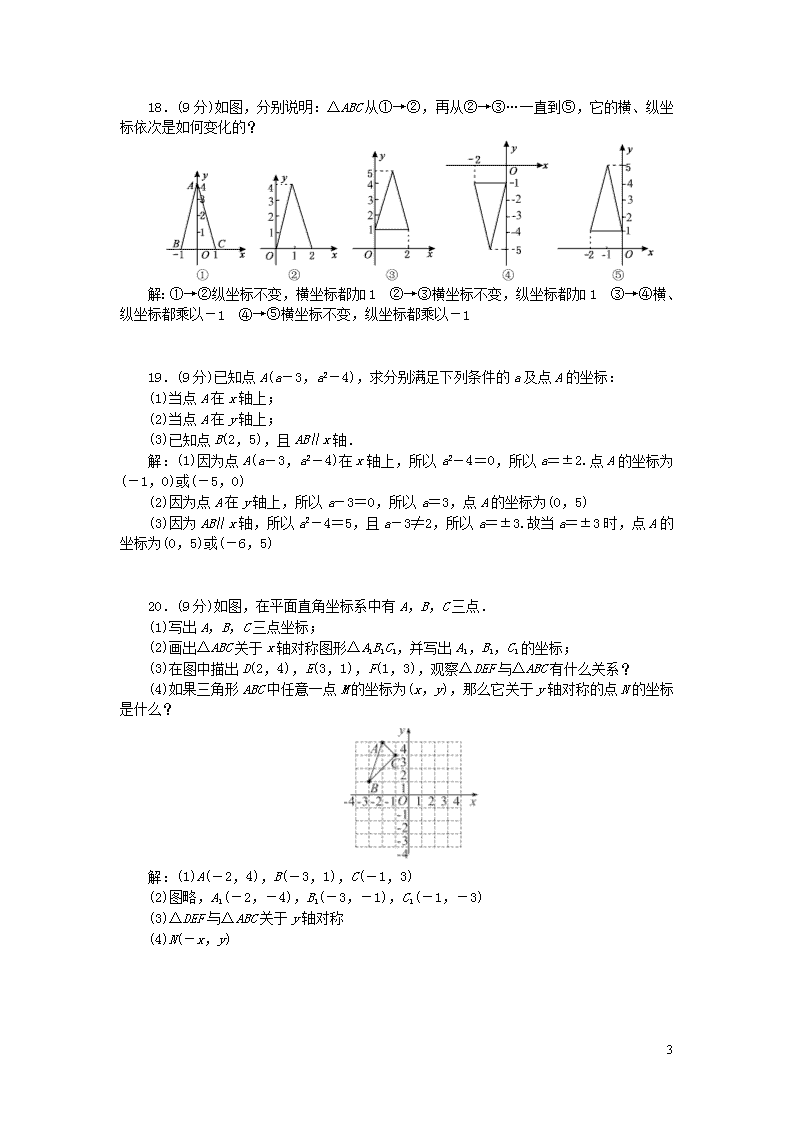
第三章检测题 (时间:100分钟 满分:120分) 一、选择题(每小题3分,共30分) 1.(聊城中考)在平面直角坐标系中,点M(-3,4)在( B ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.八(2)班有45人参加学校运动会的入场式,队伍共9排5列,如果用(2,4)表示第2排从左到右第4列站着的同学,那么站在队伍最中间的点表示为( D ) A.(15,4) B.(2,3) C.(3,0) D.(5,3) 3.若点A(m,n)在第三象限,则点B(-m,n)在( D ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 4.(湘潭中考)如图,点A的坐标(-1,2),点A关于y轴的对称点的坐标为( A ) A.(1,2) B.(-1,-2) C.(1,-2) D.(2,-1) 5.如果M(m+3,2m+4)在y轴上,那么点M的坐标是( B ) A.(-2,0) B.(0,-2) C.(1,0) D.(0,1) 6.(贵港中考)若点A(1+m,1-n)与点B(-3,2)关于y轴对称,则m+n的值是( D ) A.-5 B.-3 C.3 D.1 7.如果P点的坐标为(a,b),它关于y轴的对称点为P1,P1关于x轴的对称点为P2,已知P2的坐标为(-2,3),则点P的坐标为( B ) A.(-2,-3) B.(2,-3) C.(-2,3) D.(2,3) 8.如图,小明从点O出发,先向西走40米,再向南走30米到达点E,如果点E的位置用(-40,-30)表示,那么(10,20)表示的位置是( B ) A.点A B.点B C.点C D.点D 9.如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( B ) A.a=b B.2a+b=-1 C.2a-b=1 D.2a+b=1 10. 已知A(a,0)和B点(0,10)两点,且AB与坐标轴围成的三角形的面积等于20,则a的值为( D ) A.2 B.4 C.0或4 D.4或-4 二、填空题(每小题3分,共15分) 11.(2019·泸州)在平面直角坐标系中,点M(a,b)与点N(3,-1)关于x轴对称,则a+b的值是4. 12.如图,如果所在的位置坐标为(-1,-2),所在的位置坐标为(2,-2),则所在的位置坐标为__(-3,3)__. 13.已知点A(4,3),AB∥y轴,且AB=3,则B点的坐标为__(4,0)或(4,6)__. 14.如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12 5 ;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为__(5,-5)__. 15.(湘潭中考)阅读材料:设=(x1,y1),=(x2,y2),如果※,则x1·y2=x2·y1.根据该材料填空:已知=(2,3),=(4,m),且※,则m=__6__. 三、解答题(共75分) 16.(8分)有一张图纸被损坏,但上面有如图所示的两个标志点A(-3,1),B(-3,-3)可见,而主要建筑C(3,2)破损,请通过建立直角坐标系找到图中建筑C的位置. 解:如图: 17.(9分)图中标明了小强家附近的一些地方. (1)写出公园、游乐场和学校的坐标; (2)早晨,小强从家里出发,沿(-3,-1),(-1,-2),(0,-1),(2,-2),(1,0),(1,3),(-1,2)路线转了一下,又回到家里,写出他路上经过的地方. 解:(1)公园(3,-1),游乐场(3,2),学校(1,3) (2)邮局——移动通讯——幼儿园——消防队——火车站——学校——糖果店 5 18.(9分)如图,分别说明:△ABC从①→②,再从②→③…一直到⑤,它的横、纵坐标依次是如何变化的? 解:①→②纵坐标不变,横坐标都加1 ②→③横坐标不变,纵坐标都加1 ③→④横、纵坐标都乘以-1 ④→⑤横坐标不变,纵坐标都乘以-1 19.(9分)已知点A(a-3,a2-4),求分别满足下列条件的a及点A的坐标: (1)当点A在x轴上; (2)当点A在y轴上; (3)已知点B(2,5),且AB∥x轴. 解:(1)因为点A(a-3,a2-4)在x轴上,所以a2-4=0,所以a=±2.点A的坐标为(-1,0)或(-5,0) (2)因为点A在y轴上,所以a-3=0,所以a=3,点A的坐标为(0,5) (3)因为AB∥x轴,所以a2-4=5,且a-3≠2,所以a=±3.故当a=±3时,点A的坐标为(0,5)或(-6,5) 20.(9分)如图,在平面直角坐标系中有A,B,C三点. (1)写出A,B,C三点坐标; (2)画出△ABC关于x轴对称图形△A1B1C1,并写出A1,B1,C1的坐标; (3)在图中描出D(2,4),E(3,1),F(1,3),观察△DEF与△ABC有什么关系? (4)如果三角形ABC中任意一点M的坐标为(x,y),那么它关于y轴对称的点N的坐标是什么? 解:(1)A(-2,4),B(-3,1),C(-1,3) (2)图略,A1(-2,-4),B1(-3,-1),C1(-1,-3) (3)△DEF与△ABC关于y轴对称 (4)N(-x,y) 5 21.(10分)如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标. 解:由题意可知,折痕AD是四边形OAED的对称轴,在Rt△ABE中,AE=AO=10,AB=8,BE===6,所以CE=4,所以E(4,8).在Rt△DCE中,DC2+CE2=DE2,又因为DE=OD,所以(8-OD)2+42=OD2,解得OD=5,所以D(0,5) 22.(10分)如图,在平面直角坐标系中有三点A(-2,1),B(3,1),C(2,3). (1)在平面直角坐标系内描出点A,B,C的位置,并将各点用线段依次连接起来; (2)求出以A,B,C三点为顶点的三角形的面积; (3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由. 解:(1)图略 (2)依题意,得AB∥x轴,且AB=3-(-2)=5,所以S△ABC=×5×2=5 (3)存在.因为AB=5,S△ABP=10,所以P点到AB的距离为4.又因为点P在y轴上,所以点P的坐标为(0,5)或(0,-3) 23.(11分)如图,在平面直角坐标系中,直线l是第一、三象限的角平分线. 实验与探究: (1)由图观察可知点A(0,2)与点A1(2,0)关于直线l对称,请你在图中标明点B(3,5),C(3,-5),D(-3,-5),E(-5,0)关于直线l的对称点B1,C1,D1,E1的位置,并写出它们的坐标; 归纳与发现: 5 (2)结合图形并观察以上五组点的坐标,你会发现:坐标平面内任意一点P(a,b)关于直线l的对称点P1的坐标为__(b,a)__; 拓展与应用: (3)若点M(4,2+5y)与点N(-3,3x+1)关于第一、三象限的角平分线对称,求点(x,y)的坐标. 解:(1)B1(5,3),C1(-5,3),D1(-5,-3),E1(0,-5) (2)(b,a) (3)根据任意一点P(a,b)关于直线y=x的对称点P1的坐标为 (b,a)可知,2+5y=-3,3x+1=4,解得x=1,y=-1,所以点(x,y)的坐标为(1,-1) 5查看更多