2020八年级数学上册第2章特殊三角形2

2020八年级数学上册第2章特殊三角形2

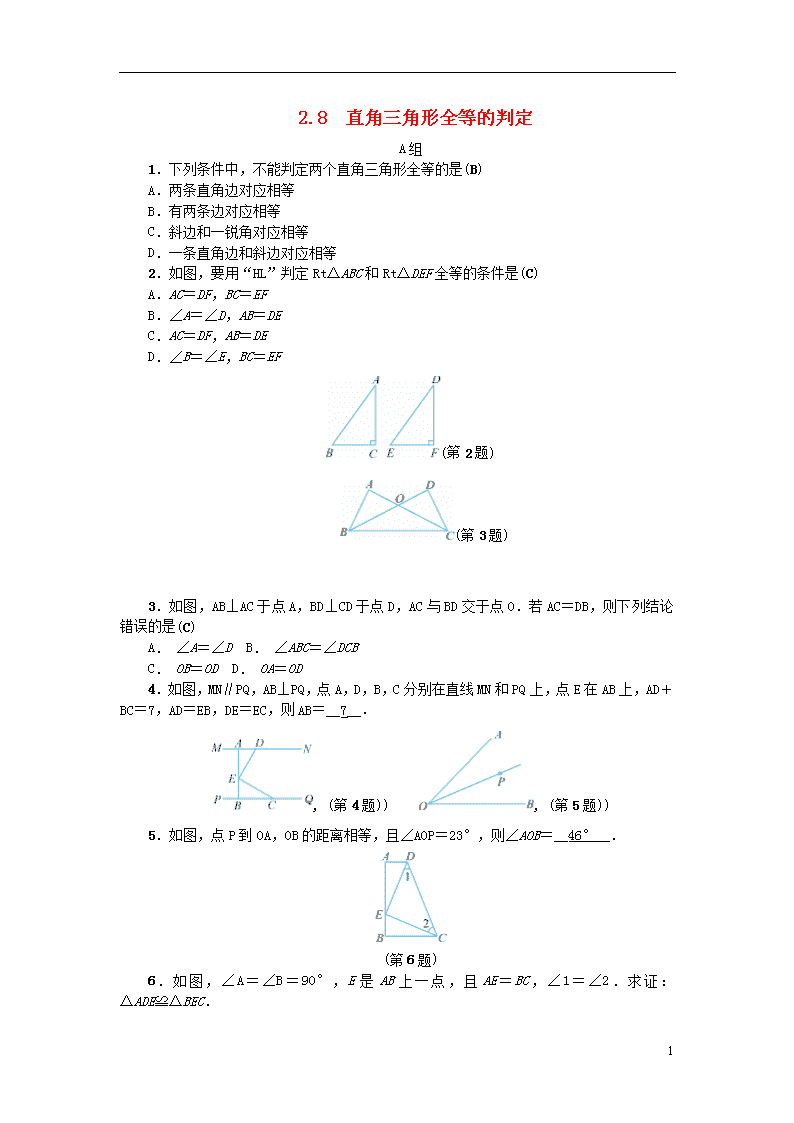
‎2.8 直角三角形全等的判定 A组 ‎1．下列条件中，不能判定两个直角三角形全等的是(B)‎ A．两条直角边对应相等 B．有两条边对应相等 C．斜边和一锐角对应相等 D．一条直角边和斜边对应相等 ‎2．如图，要用“HL”判定Rt△ABC和Rt△DEF全等的条件是(C)‎ A．AC＝DF，BC＝EF B．∠A＝∠D，AB＝DE C．AC＝DF，AB＝DE D．∠B＝∠E，BC＝EF ‎(第2题)‎ ‎　　(第3题)‎ ‎3．如图，AB⊥AC于点A，BD⊥CD于点D，AC与BD交于点O．若AC＝DB，则下列结论错误的是(C)‎ A． ∠A＝∠D B． ∠ABC＝∠DCB C． OB＝OD D． OA＝OD ‎4．如图，MN∥PQ，AB⊥PQ，点A，D，B，C分别在直线MN和PQ上，点E在AB上，AD＋BC＝7，AD＝EB，DE＝EC，则AB＝__7__．‎ ‎, (第4题))　　, (第5题))‎ ‎5．如图，点P到OA，OB的距离相等，且∠AOP＝23°，则∠AOB＝__46°__．‎ ‎(第6题)‎ ‎6．如图，∠A＝∠B＝90°，E是AB上一点，且AE＝BC，∠1＝∠2．求证：△ADE≌△BEC．‎ 4‎ ‎【解】　∵∠1＝∠2，∴DE＝EC．‎ 又∵∠A＝∠B＝90°，AE＝BC，‎ ‎∴Rt△ADE≌Rt△BEC(HL)．‎ ‎7．如图，AD平分∠BAC，DE⊥AB于点E，DF⊥AC ‎(第7题)‎ 于点F，且DB＝DC，求证：EB＝FC．‎ ‎【解】　∵AD平分∠BAC，DE⊥AB，DF⊥AC，‎ ‎∴DE＝DF，∠BED＝∠CFD＝90°．‎ 在Rt△DBE和Rt△DCF中，‎ ‎∵∴Rt△DBE≌Rt△DCF(HL)，‎ ‎∴EB＝FC．‎ B组 ‎8．如图，∠C＝90°，AC＝10，BC＝5，AX⊥AC，点P和点Q分别在线段AC和射线AX上运动，且AB＝PQ，当AP＝5或10时，△ABC与△APQ全等．‎ ‎【解】　∵AX⊥AC，‎ ‎∴∠PAQ＝90°，‎ ‎∴∠C＝∠PAQ＝90°．‎ 分两种情况：‎ ‎①当PA＝BC＝5时，‎ 在Rt△ABC和Rt△QPA中，∵ ‎∴Rt△ABC≌Rt△QPA(HL)．‎ ‎②当PA＝AC＝10时，‎ 在Rt△ABC和Rt△PQA中，‎ ‎∵ ‎∴Rt△ABC≌Rt△PQA(HL)．‎ 综上所述，当AP＝5或10时，△ABC与△APQ全等．‎ ‎,(第8题))　　,(第9题))‎ 4‎ ‎9．如图，在长方形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F，连结EF．若AB＝6，BC＝，则FD的长为__4__．‎ ‎【解】　∵E是AD的中点，∴AE＝DE．‎ ‎∵△ABE沿BE折叠后得到△GBE，‎ ‎∴AE＝GE，AB＝GB．∴DE＝GE．‎ ‎∵四边形ABCD是长方形，∴∠A＝∠D＝90°，‎ ‎∴∠EGF＝180°－∠EGB＝180°－∠A＝90°．‎ 在Rt△EDF和Rt△EGF中，∵ ‎∴Rt△EDF≌Rt△EGF(HL)．∴DF＝GF．‎ 设DF＝x，则BF＝6＋x，CF＝6－x．‎ 由勾股定理，得()2＋(6－x)2＝(6＋x)2，‎ 解得x＝4．‎ ‎10．如图，在Rt△ABC中，∠C＝90°，BD是Rt△ABC的一条角平分线，点O，E，F分别在BD，BC，AC上，且四边形OECF是正方形．‎ ‎(1)求证：点O在∠BAC的平分线上．‎ ‎(2)若AC＝5，BC＝12，求OE的长．‎ ‎,(第10题))　,(第10题解))‎ ‎【解】　(1)如解图，过点O作OM⊥AB于点M．‎ ‎∵四边形OECF是正方形，‎ ‎∴OE＝EC＝CF＝OF，OE⊥BC，OF⊥AC．‎ ‎∵BD平分∠ABC，OM⊥AB，OE⊥BC，‎ ‎∴OM＝OE，∴OM＝OF．‎ ‎∵OM⊥AB，OF⊥AC，‎ ‎∴点O在∠BAC的平分线上．‎ ‎(2)在Rt△ABC中，∵∠C＝90°，AC＝5，BC＝12，‎ ‎∴AB＝13．‎ ‎∵BE＝BC－CE，AF＝AC－CF，CE＝CF＝OE，‎ ‎∴BE＝12－OE，AF＝5－OE．‎ 易证BE＝BM，AM＝AF．‎ ‎∵BM＋AM＝AB，‎ ‎∴BE＋AF＝13，‎ ‎∴(12－OE)＋(5－OE)＝13，‎ 解得OE＝2．‎ 数学乐园 ‎11．如图①，点A，E，F，C在同一条直线上，AE＝CF，过点E，F分别作DE⊥AC，BF⊥AC，且AB＝CD，AC与BD交于点G．‎ ‎(1)求证：BD平分EF．‎ 4‎ ‎(2)若将△DEC的边EC沿AC方向移动变为图②，其余的条件不变，上述结论是否仍成立？请说明理由．‎ ‎(第11题)‎ ‎【解】　(1)∵AE＝CF，∴AE＋EF＝CF＋EF，‎ ‎∴AF＝CE．‎ ‎∵DE⊥AC，BF⊥AC，∴∠AFB＝∠CED＝90°．‎ 又∵AB＝CD，∴Rt△ABF≌Rt△CDE(HL)．‎ ‎∴BF＝DE．‎ 又∵∠BGF＝∠DGE，‎ ‎∴△BFG≌△DEG(AAS)．‎ ‎∴GF＝GE，即BD平分EF．‎ ‎(2)结论仍成立．理由如下：‎ ‎∵DE⊥AC，BF⊥AC，∴∠AFB＝∠CED＝90°．‎ ‎∵AE＝CF，∴AE－EF＝CF－EF，即AF＝CE．‎ ‎∵AB＝CD，∴Rt△ABF≌Rt△CDE(HL)．‎ ‎∴BF＝DE．‎ 又∵∠BGF＝∠DGE，‎ ‎∴△BFG≌△DEG(AAS)．‎ ‎∴GF＝GE，即BD平分EF．‎ 4‎