- 2021-11-01 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020八年级数学上册第2章特殊三角形2
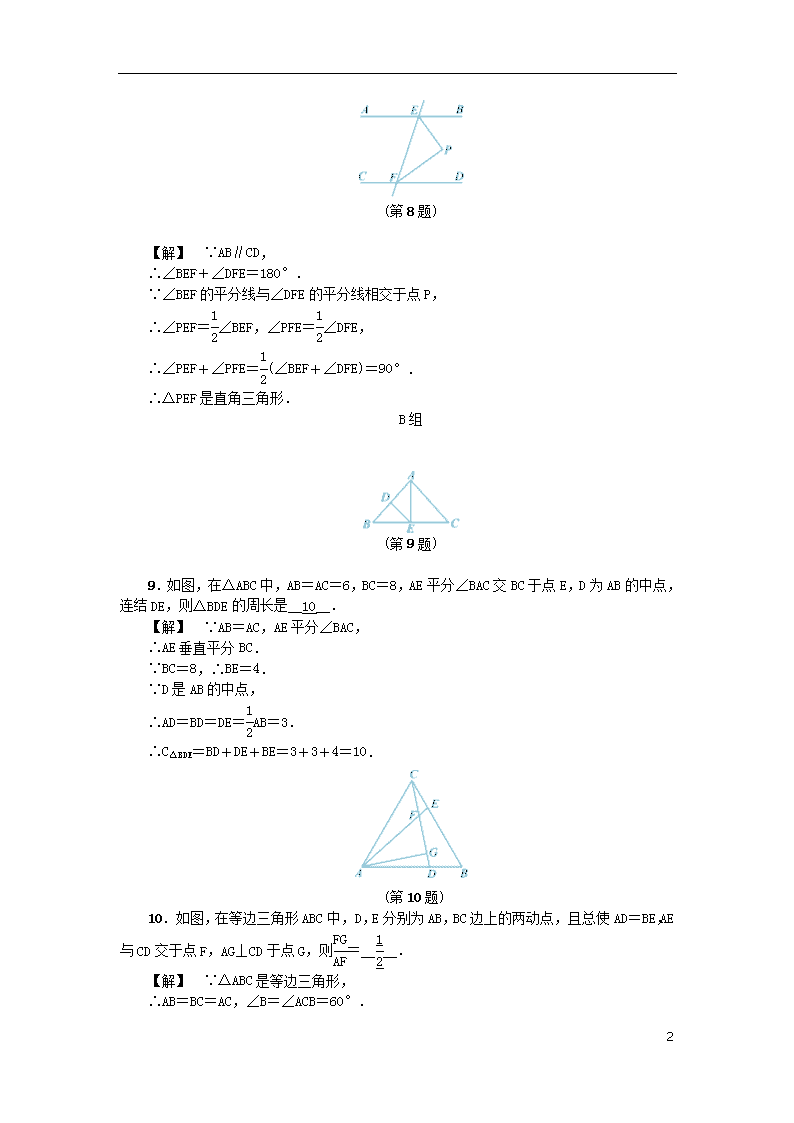
2.6 直角三角形(二) A组 1.具备下列条件的△ABC中,不是直角三角形的是(D) A. ∠A+∠B=∠C B. ∠A=2∠B=2∠C C. ∠A∶∠B∶∠C=1∶2∶3 D. ∠A=∠B=3∠C 2.已知一个三角形的其中一个角等于另两个角的差,则这个三角形一定是直角三角形. (第3题) 3.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于点E,交BC的延长线于点F.若∠F=30°,DE=1,则BE的长是__2__. 4.等腰三角形一腰上的高线等于这条腰的一半,则这个等腰三角形的顶角的度数为30°或150°. 5.在△ABC中,2∠B=∠A+∠C,最小角∠A=30°,最长边的中线为8 cm,则最短边的长为__8__cm. 6.直角三角形斜边上的高线长与中线长分别为5 cm和6 cm,则它的面积为__30__cm2. 7.如图,CE⊥AD,垂足为E,∠A=∠C.求证:△ABD是直角三角形. (第7题) 【解】 ∵CE⊥AD, ∴∠CED=90°, ∴∠C+∠D=90°. 又∵∠A=∠C, ∴∠A+∠D=90°, ∴△ABD是直角三角形. 8.如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.求证:△PEF是直角三角形. 5 (第8题) 【解】 ∵AB∥CD, ∴∠BEF+∠DFE=180°. ∵∠BEF的平分线与∠DFE的平分线相交于点P, ∴∠PEF=∠BEF,∠PFE=∠DFE, ∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°. ∴△PEF是直角三角形. B组 (第9题) 9.如图,在△ABC中,AB=AC=6,BC=8,AE平分∠BAC交BC于点E,D为AB的中点,连结DE,则△BDE的周长是__10__. 【解】 ∵AB=AC,AE平分∠BAC, ∴AE垂直平分BC. ∵BC=8,∴BE=4. ∵D是AB的中点, ∴AD=BD=DE=AB=3. ∴C△BDE=BD+DE+BE=3+3+4=10. (第10题) 10.如图,在等边三角形ABC中,D,E分别为AB,BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则=____. 【解】 ∵△ABC是等边三角形, ∴AB=BC=AC,∠B=∠ACB=60°. 5 ∵AD=BE,∴CE=BD. 在△ACE和△CBD中, ∵ ∴△ACE≌△CBD(SAS).∴∠CAE=∠BCD. ∴∠AFG=∠CAF+∠ACF=∠BCD+∠ACF=∠ACB=60°. ∵AG⊥CD,∴∠FAG=30°.∴=. (第11题) 11.如图,在四边形ABCD中,∠ABC=∠ADC=90°,M,N分别是对角线AC,BD的中点,连结MN. (1)试猜想MN与BD的位置关系,并证明你的结论. (2)如果∠BCD=45°,BD=2,求MN的长. 【解】 (1)MN⊥BD.证明如下: 连结BM,DM. ∵∠ADC=90°,M是AC的中点, ∴AC=2DM=2CM. 同理,AC=2BM=2CM,∴BM=DM. ∵N是BD的中点,∴MN⊥BD. (2)由(1),得BM=CM,DM=CM, ∴∠BCM=∠CBM,∠DCM=∠CDM. ∵∠AMB是△BCM的一个外角, ∴∠AMB=∠BCM+∠CBM=2∠BCM. 同理,∠AMD=2∠DCM. ∵∠BCD=45°,∴∠BCM+∠DCM=45°. ∴∠BMD=∠AMB+∠AMD=2(∠BCM+∠DCM)=90°.∴△BMD是直角三角形. ∵N是BD的中点,BD=2,∴MN=BD=1. 12.如图,AD,BF分别是△ABC的高线与角平分线,BF,AD交于点E,∠1=∠2.求证:△ABC是直角三角形. (第12题) 【解】 ∵BF是△ABC的角平分线, ∴∠ABF=∠CBF. ∵AD是△ABC的高线, 5 ∴∠ADB=90°, ∴∠CBF+∠BED=90°. ∵∠1=∠2=∠BED,∴∠ABF+∠2=90°, ∴∠BAC=90°,∴△ABC是直角三角形. (第13题) 13.如图,在△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F,连结DF.求证:AB垂直平分DF. 【解】 ∵∠ACB=90°,AC=BC, ∴∠CAB=∠CBA=45°,∠CAD+∠CDE=90°. ∵CE⊥AD,∴∠CED=90°. ∴∠CDE+∠DCE=90°. ∴∠CAD=∠DCE,即∠CAD=∠BCF. ∵BF∥AC,∴∠CBF+∠ACB=180°, ∴∠CBF=180°-∠ACB=90°. ∴∠CBF=∠ACD. 在△ACD和△CBF中,∵ ∴△ACD≌△CBF(ASA). ∴CD=BF. ∵D为BC的中点, ∴CD=BD,∴BD=BF. ∵BF∥AC, ∴∠ABF=∠CAB=∠DBA=45°. ∴AB垂直平分DF. 数学乐园 14.如图,在△ABC中,AB=AC,∠A=90°,CD平分∠ACB,点E在AC上,且AE=AD,EF⊥CD交BC于点F,交CD于点O.求证:BF=2AD. (第14题) 导学号:91354012 5 【解】 连结DF,过点D作DG⊥BC于点G. ∵∠A=90°,AD=AE,AB=AC, ∴∠ADE=∠AED=45°,∠B=∠ACB=45°, ∴∠ADE=∠B,∴DE∥BC, ∴∠EDC=∠BCD. ∵CD平分∠ACB,∴∠BCD=∠ACD. ∴∠EDC=∠ACD.∴DE=EC. ∵EF⊥CD,∴EF垂直平分CD. ∴FD=FC.∴∠FDC=∠FCD. ∴∠FDC=∠ACD.∴DF∥AC. ∴∠DFB=∠ACB=45°. ∴∠B=∠BFD=45°. ∴BD=DF,∠BDF=90°. ∴△DBF为等腰直角三角形. ∵DG⊥BF,∴DG为斜边BF上的中线, ∴DG=BF. ∵CD平分∠ACB,∠A=∠DGC=90°, ∴AD=DG.∴AD=BF,即BF=2AD. 5查看更多