八年级下数学课件：17-1 勾股定理——探索勾股定理 （共25张PPT）_人教新课标

八年级下数学课件：17-1 勾股定理——探索勾股定理 （共25张PPT）_人教新课标

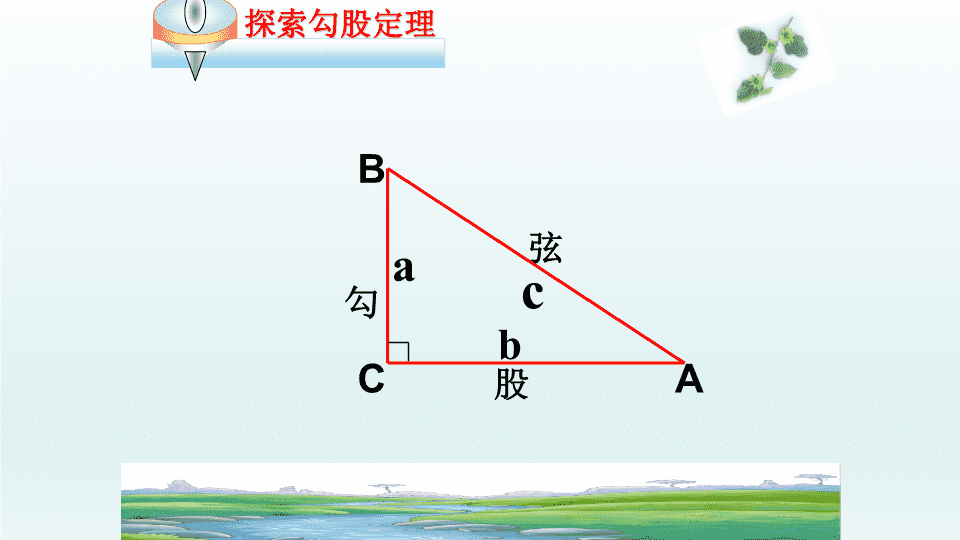
探 索 勾 股 定 理 在数学的天地里， 　　　　 ——毕达哥拉斯 重要的不是我们知道什么， 而是我们怎么知道什么。 ca b 勾 股 弦 A B C 动手操作： 你能用四个全等的直角三角形拼出 正方形吗？ a b c a b c a b c a b c 黄实 c c c c a a a a b ? 赵爽弦图 a a a a b b b b c cc c • 议一议：观察并计算，判断锐角三角形，钝角 三角形三边的长度是否满足a2 +b2=c2 ？ 如果直角三角形两直角边分别为a、b， 斜边为c，那么 a2 + b2 = c2 （直角三角形两直角边的平方和等于斜边的平方） 勾股定理 ca b 勾 股 弦 A B C ∵在Rt △ABC中， ∠C＝90° ∴ a2 + b2 = c2 几何语言： 例：在Rt △ ABC中，∠C=90° 1）如果 b=4 ， c =5 ， 那么a = _____ 3）如果 a =6 ， b=8 ， 那么 c = ____ 已知直角三角形的任意两边可以求出第三边。 5 20 10 a b c 22 ba  22 bc  22 ac  求下图中表示面积的未知数x的值. 81 144 x 求下图中表示面积的未知数y的值. y 625 576 求直角三角形中未知边的长。 x 108 求直角三角形中未知边的长。 12 5 x 　　勾股定理学习完之后，老师布置了这 样一道题目：“如果一个直角三角形的两 条边长分别是3厘米和4厘米，那么这个三 角形的第三边是多少?”，　小明看完后不 假思索的写下了这样的解答过程： 　解：设第三边的长为Ｘ厘米．由勾股定理可得： 　　　　　 ３ 　＋４　＝Ｘ 　　　　　　　∴Ｘ ＝２５ 　　　　　　又∵Ｘ＞０ 　　　　　　　 ∴Ｘ＝５ 你认为他的做法正确吗？如果不正确，应如何改正？ ２２ ２ ２ 9 米 在台风“麦莎”的袭击中，一棵大树在离地 面9米处断裂，树的顶部落在离树根底部12米 处。这棵树折断之前有多高？ 12米 A B C 两千多年前，古希腊有个哥拉 斯学派，他们首先发现了勾股定理，因此 在国外人们通常称勾股定理为毕达哥拉斯 年希腊曾经发行了一枚纪念票。 定理。为了纪念毕达哥拉斯学派，1955 国家之一。早在三千多年前， 国家之一。早在三千多年前， 国家之一。早在三千多年前， 国家之一。早在三千多年前， 国家之一。早在三千多年前， 国家之一。早在三千多年前， 国家之一。早在三千多年前， 国家之一。早在三千多年前 两千多年前，古希腊有个毕达哥拉斯 学派，他们首先发现了勾股定理，因此在 国外人们通常称勾股定理为毕达哥拉斯定 理。为了纪念毕达哥拉斯学派，1955年 希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的 国家之一。早在三千多年前，周 朝数学家商高就提出，将一根直 尺折成一个直角，如果勾等于三， 股等于四，那么弦就等于五，即 “勾三、股四、弦五”，它被记 载于我国古代著名的数学著作 《周髀算经》中。 这是1955年希腊 为纪念一位数学家曾 经发行的邮票。 34 5 2 2 23 +4 = 5 邮票的秘密 观察这枚邮票 图案小方格的个数， 你有什么发现? 勾股数： 3, 4, 5 6, 8, 10 5,12,13 9,12,15 ……. 1 1 欣赏美丽的勾股树 2、本节课主要运用什么方 法来解决一些简单的实际 问题？ 1、经过本节课的学习，你 有哪些收获？ 小 结 经过本节课的学习， 你有哪些收获？ 请和我们一起分享. 1、课本69页第1、2题 2、通过查找、翻阅有关勾股定理的 多种证明方法的资料，以小组为单位 办一份手抄报．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 天空的幸福是穿一身蓝 森林的幸福是披一身绿 阳光的幸福是如钻石般耀眼 老师的幸福是因为认识了你们 愿你们努力进取，永不言败 致我亲爱的同学们: 谢 谢 大 家