- 2021-11-01 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
沪科版八年级数学上册期末测试题2(含答案)
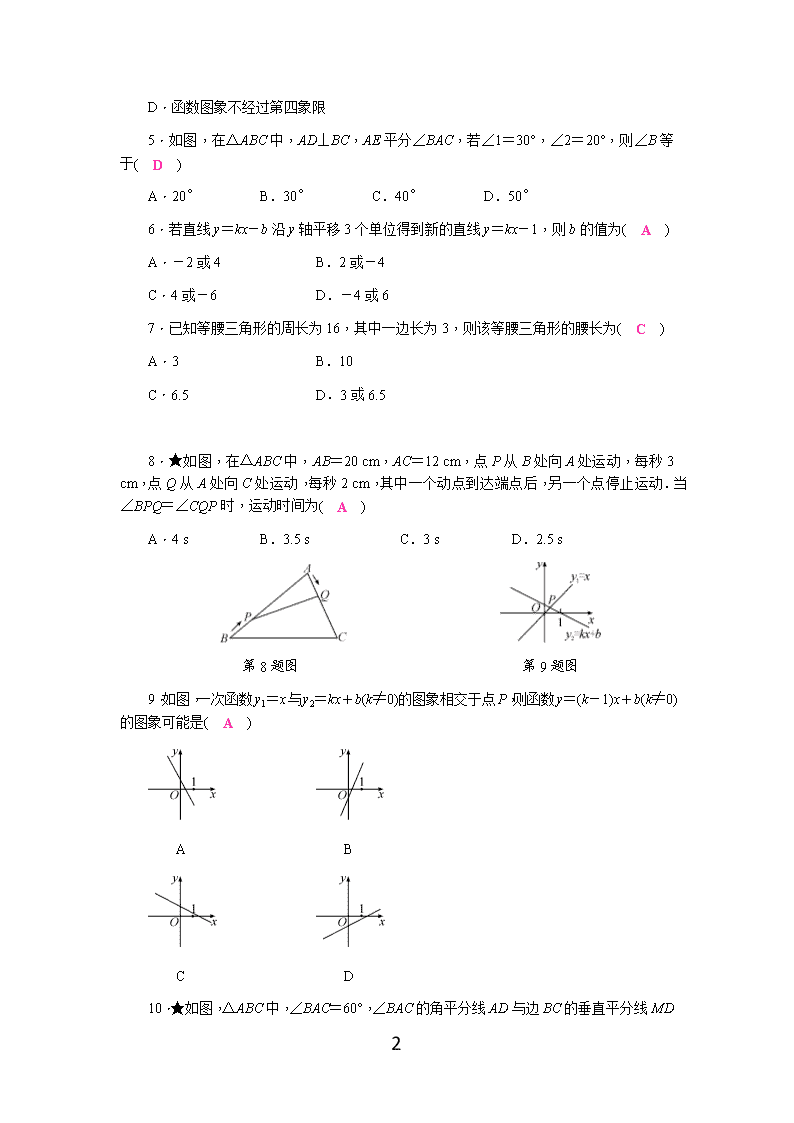
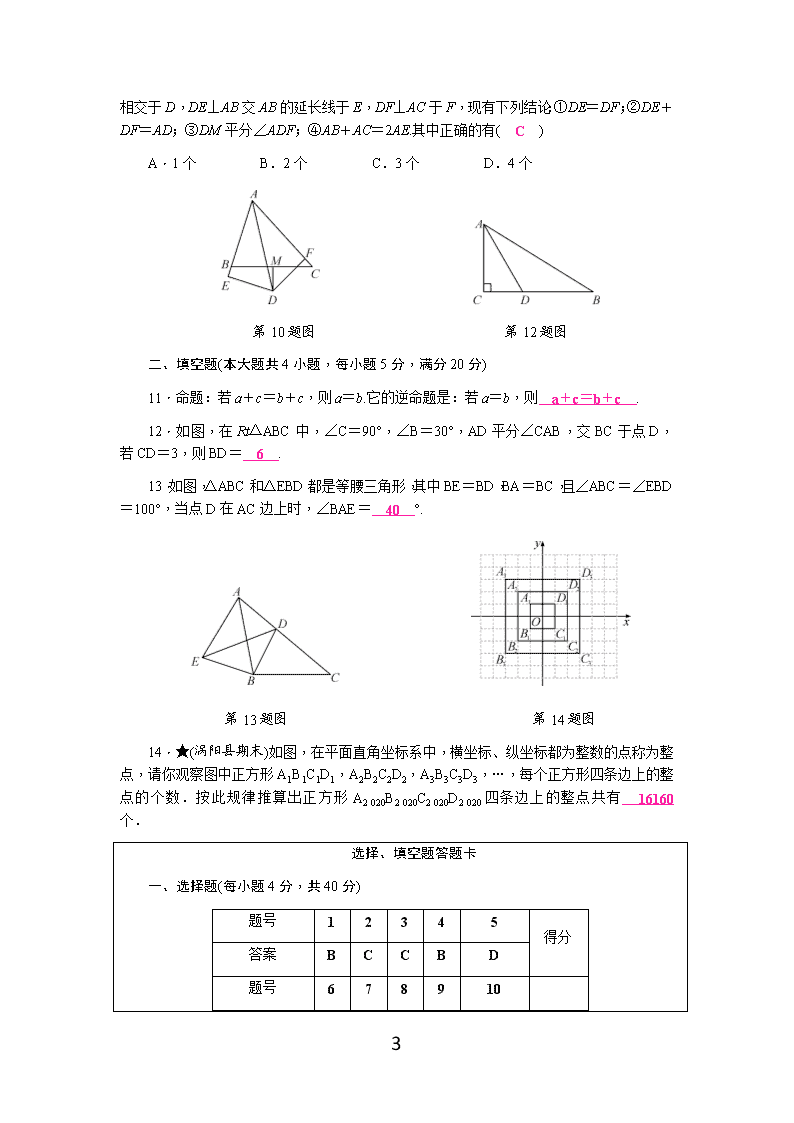
沪科版八年级数学上册期末测试题2(含答案) (考试时间:120分钟 满分:150分) 分数:__________ 一、选择题(本大题共10小题,每小题4分,满分40分) 每小题都给出A、B、C、D四个选项,其中只有一个是正确的. 1.在平面直角坐标系中,点P(-2 020,2 019)所在的象限是( B ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( C ) A B C D 3.如图,∠BDA=∠BDC,现添加以下哪个条件不能判定△ABD≌△CBD的是( C ) A.∠A=∠C B.∠ABD=∠CBD C.AB=CB D.AD=CD 第3题图 第5题图 4.对于一次函数y=x+2,下列结论错误的是( B ) A.函数值随自变量增大而增大 B.函数图象与x轴交点坐标是(0,2) C.函数图象与x轴正方向成45°角 10 D.函数图象不经过第四象限 5.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B等于( D ) A.20° B.30° C.40° D.50° 6.若直线y=kx-b沿y轴平移3个单位得到新的直线y=kx-1,则b的值为( A ) A.-2或4 B.2或-4 C.4或-6 D.-4或6 7.已知等腰三角形的周长为16,其中一边长为3,则该等腰三角形的腰长为( C ) A.3 B.10 C.6.5 D.3或6.5 8.★如图,在△ABC中,AB=20 cm,AC=12 cm,点P从B处向A处运动,每秒3 cm,点Q从A处向C处运动,每秒2 cm,其中一个动点到达端点后,另一个点停止运动.当∠BPQ=∠CQP时,运动时间为( A ) A.4 s B.3.5 s C.3 s D.2.5 s 第8题图 第9题图 9.如图,一次函数y1=x与y2=kx+b(k≠0)的图象相交于点P,则函数y=(k-1)x+b(k≠0)的图象可能是( A ) A B C D 10.★如图,△ABC中,∠BAC=60°,∠BAC的角平分线AD与边BC的垂直平分线MD 10 相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE.其中正确的有( C ) A.1个 B.2个 C.3个 D.4个 第10题图 第12题图 二、填空题(本大题共4小题,每小题5分,满分20分) 11.命题:若a+c=b+c,则a=b.它的逆命题是:若a=b,则 a+c=b+c . 12.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=3,则BD= 6 . 13.如图,△ABC和△EBD都是等腰三角形,其中BE=BD,BA=BC,且∠ABC=∠EBD=100°,当点D在AC边上时,∠BAE= 40 °. 第13题图 第14题图 14.★(涡阳县期末)如图,在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,每个正方形四条边上的整点的个数.按此规律推算出正方形A2 020B2 020C2 020D2 020四条边上的整点共有 16160 个. 选择、填空题答题卡 一、选择题(每小题4分,共40分) 题号 1 2 3 4 5 得分 答案 B C C B D 题号 6 7 8 9 10 10 答案 A C A A C 二、填空题(每小题5分,共20分)得分:______ 11. a+c=b+c 12. 6 13. 40 14. 16160 三、(本大题共2小题,每小题8分,满分16分) 15.在平面直角坐标系中,已知点M(m-1,2m+3). (1)若点M在y轴上,求m的值; (2)若点M在第一、三象限的角平分线上,求m的值. 解:(1)由题意得m-1=0, 解得m=1. (2)由题意得m-1=2m+3, 解得m=-4. 16.(涡阳县期末)如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5,BE⊥AC于E,求BE的长. 解:∵AD⊥BC, BE⊥AC, ∴在△ABC中AD是以BC为底的△ABC的高,BE是以AC为底的△ABC的高. ∴S△ABC=AC·BE,S△ABC=BC·AD, ∴AC·BE=BC·AD, ∴BE==. 10 四、(本大题共2小题,每小题8分,满分16分) 17.(合肥庐阳区期末)如图,已知AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD,求证:△OAB是等腰三角形. 证明:∵AC⊥BC,BD⊥AD, ∴∠D=∠C=90°. 在Rt△ABD和Rt△BAC中, ∴Rt△ABD≌Rt△BAC,(HL) ∴∠DBA=∠CAB, ∴OA=OB, 即△OAB是等腰三角形. 18.如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F, (1)求∠F的度数; (2)若CD=5,求DF的长. 解:(1)∵△ABC是等边三角形, ∴∠B=60°. ∵DE∥AB, ∴∠EDC=∠B=60°. ∵EF⊥DE, 10 ∴∠DEF=90°, ∴∠F=90°-∠EDC=30°. (2)∵∠ACB=60°,∠EDC=60°, ∴△EDC是等边三角形. ∴ED=DC=5. ∵∠DEF=90°,∠F=30°, ∴DF=2DE=10. 五、(本大题共2小题,每小题10分,满分20分) 19.(东至县期末)在边长均为1的正方形网格中建立如图所示的平面直角坐标系,点A,点B的坐标分别为(2,1),(5,0). (1)画出△OAB关于x轴的对称图形; (2)在平面直角坐标系内找一点D(不与点B重合),使△OAD与△OAB全等,请直接写出所有可能的点D的坐标. 解:(1)如图所示,△OA′B即为所求. (2)如图所示,△OAD′,△OAD″,△OAD′″即为所求,其中点D的坐标为(-1,-3)或(3,4)或(-3,1). 20.(安庆期末)平面直角坐标系中,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:「P」,即「P」=|x|+|y|. (1)求点A(-1,3)的勾股值「A」; (2)若点B在第一象限且满足「B」=3,求满足条件的所有B点与坐标轴围成的图形的面积. 10 解:(1)「A」=|-1|+|3|=4. (2)设点B(x,y),由「B」=3且在第一象限知,x+y=3(x>0,y>0), 即y=-x+3(x>0,y>0). 故所有点B与坐标轴围成的图形如图所示的三角形, 故其面积为×3×3=. 六、(本题满分12分) 21.如图,已知直线y=kx+b(k≠0)经过点A(5,0),B(1,4). (1)求直线AB的表达式; (2)若直线y=2x-4与直线AB相交于点C,求点C的坐标; (3)根据图象,写出关于x的不等式2x-4>kx+b的解集. 解:(1)∵直线y=kx+b(k≠0)经过点A(5,0),B(1,4), ∴ 解得 ∴直线AB的表达式为y=-x+5. (2)∵直线y=2x-4与直线AB相交于点C, ∴解得 10 ∴点C(3,2). (3)根据图象可得x>3. 七、(本题满分12分) 22.(蚌埠期末)2019年3月5日,政府工作报告中有关“通信费用再降”的报告指出:移动网络流量平均资费再降低20%以上,在全国实行“携号转网”,规范套餐设置,使降费实实在在、消费者明明白白.某通信运营商积极响应国家号召,推出A,B,C三种手机通话的收费方式,如表所示. 收费方式 月通话费/元 包时通话时间/h 超时费/(元/min) A 30 25 0.1 B 50 50 0.1 C 100 不限时 (1)设月通话时间为x小时,则方案A,B,C的收费金额y1,y2,y3都是x的函数,请分别求出y1和y2函数表达式; (2)若选择方式A最省钱,求月通话时间x的取值范围; (3)小明、小华今年5月份通话费均为80元,但小明比小华通话时间长,求小明该月的通话时间. 解:(1)∵0.1元/min=6元/h, ∴由题意可得, y1=y2= (2)若选择方式A最省钱,则6x-120≤50,解得x≤. 若选择方式A最省钱,则月通话时间x的取值范围为0≤x<. (3)∵小明、小华今年5月份通话费均为80元,但小明比小华通话时间长, ∴小华选择的是方式A,小明选择的是方式B, 将y=80分别代入y2= 可得6x-250=80, 10 解得x=55, ∴小明该月的通话时间为55小时. 八、(本题满分14分) 23.(肥西县期末)如图,在△ABC中,BE⊥AC于点E,BC的垂直平分线分别交AB,BE于点D,G,垂足为H,CD⊥AB,CD交BE于点F. (1)求证:△BDF≌△CDA; (2)若DF=DG,求证:①BE平分∠ABC;②BF=2CE. 证明:(1)∵DH垂直平分BC, ∴BD=CD. ∵BE⊥AC,BA⊥CD, ∴∠A+∠DBF=90°, ∠DBF+∠DFB=90°, ∴∠A=∠DFB,且BD=CD,∠ADC=∠BDF, ∴△BDF≌△CDA.(AAS) (2)①∵DF=DG, ∴∠DGF=∠DFG. ∵∠BGH=∠DGF. ∴∠DGF=∠DFG=∠BGH. ∵∠DBF+∠DFB=90°,∠FBC+∠BGH=90°, ∴∠DBF=∠FBC, ∴BE平分∠ABC. ②∵∠DBF=∠CBF,BE=BE, ∠AEB=∠BEC=90°, ∴△ABE≌△CBE,(ASA) 10 ∴AE=CE, ∴AC=2CE. ∵△ADC≌△FDB, ∴BF=AC,∴BF=2CE. 10查看更多