2019学年八年级数学下学期期末综合复习资料试题（三）

2019学年八年级数学下学期期末综合复习资料试题（三）

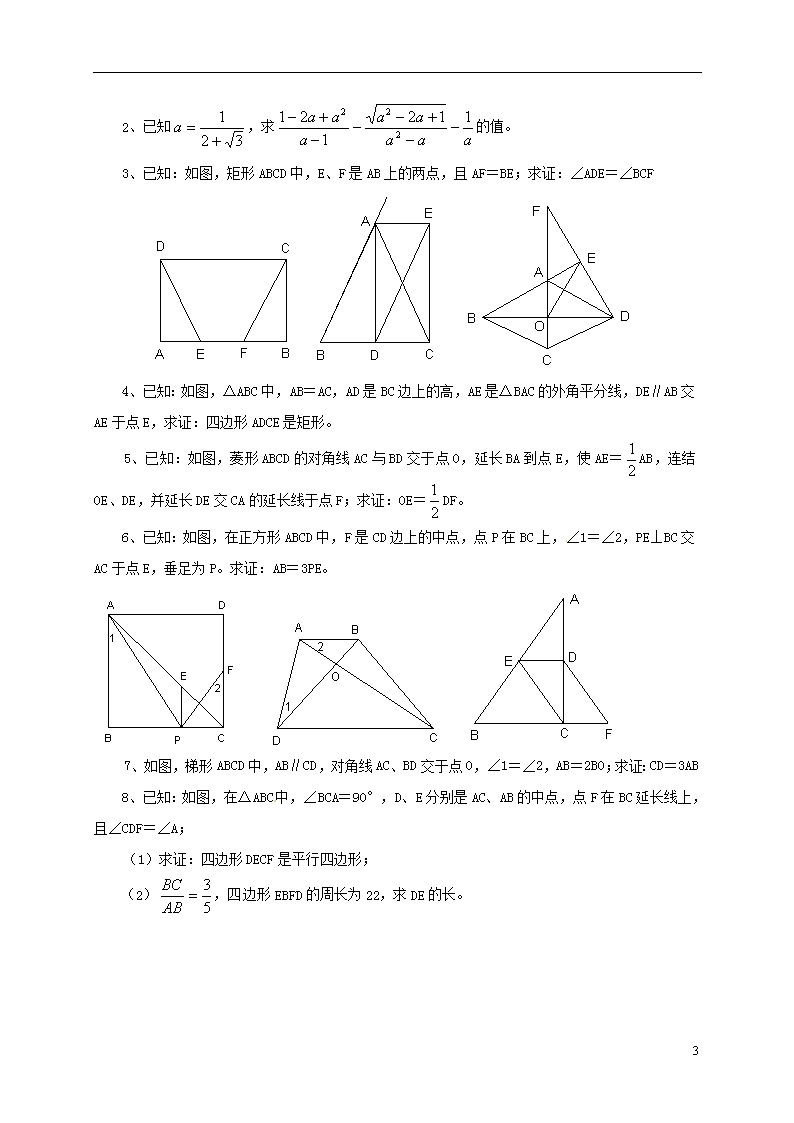
八年级下学期期末数学综合复习资料（三）‎ 一、填空题：‎ ‎1、计算＝ ； ； 。‎ ‎2、的倒数是 。‎ ‎3、当 时，二次根式有意义。‎ ‎4、当＜0时，＝ 。‎ ‎5、在△ABC中，D、E分别是AB、AC的中点，若BC＝‎8cm，则DE＝ 。‎ ‎6、菱形的一个内角是60°，边长为‎5cm，则这个菱形较短的对角线长是 。‎ ‎7、如果梯形的两底之比为2∶5，中位线长‎14cm，那么较大的底长为 。‎ ‎8、已知线段＝‎4cm，＝‎9cm，线段是、的比例中项，则＝ 。‎ ‎9、已知线段＝‎2cm，＝‎3cm，＝‎6cm，是、、的第四比例项，那么＝ 。‎ ‎10、梯形的中位线长为‎6cm，上底长为‎4cm，那么这个梯形的下底长为 。‎ ‎11、矩形ABCD的对角线AC、BD相交于点O，∠AOB＝60°，AB＝3.6，那么AC的长为 。‎ ‎12、如图，DE∥BC且DB＝AE，若AB＝5，AC＝10，则AE的长为 ；若BC＝10，则DE的长为 。‎ ‎ ‎ ‎13、如图，直角梯形ABCD的一条对角线AC将梯形分成两个三角形，△ABC是边长为10的等边三角形，则梯形ABCD的中位线EF＝ 。‎ ‎14、矩形ABCD中，CE⊥BD，E为垂足，∠DCE∶∠ECB＝3∶1，那么∠ACE＝ 度。‎ 二、选择题：‎ ‎1、下列图形中，不是中心对称图形的是（ ）‎ A、菱形 B、平行四边形 C、正方形 D、等腰梯形 ‎2、如果一个多边形的内角和等于720°，那么这个多边形是（ ）‎ A、正方形 B、三角形 C、五边形 D、六边形 4‎ ‎3、顺次连结任意四边形各边中点所得的四边形是（ ）‎ A、平行四边形 B、矩形 C、菱形 D、正方形 ‎4、化简的结果为（ ）‎ A、 B、 C、 D、‎ ‎5、当1＜＜2时，化简的结果是（ ）‎ A、2 B、—‎2 C、—4 D、2－4‎ ‎6、下列两个三角形一定相似的是（ ）‎ A、两个直角三角形 B、两个锐角三角形 ‎ C、两个等腰三角形 D、两个等边三角形 ‎7、下列性质中，平行四边形不一定具备的是（ ）‎ A、邻角互补 B、对角互补 C、对边相等 D、对角线互相平分 ‎8、下列命题正确的是（ ）‎ A、两条对角线相等的四边形是矩形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线互相垂直平分的四边形是正方形 ‎ D、两条对角线相等的梯形是等腰梯形 ‎9、下列二次根式中与是同类二次根式的是（ ）‎ A、 B、 C、 D、‎ ‎10、下列命题中真命题是（ ）‎ A、两个直角三角形是相似三角形 B、两个等边三角形是相似三角形 C、两个等腰三角形是相似三角形 D、等边三角形是中心对称图形 ‎11、矩形具有而菱形不一定具有的性质是（ ）‎ A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对边相等 三、解答题：‎ ‎1、已知：，。求的值。‎ 4‎ ‎2、已知，求的值。‎ ‎3、已知：如图，矩形ABCD中，E、F是AB上的两点，且AF＝BE；求证：∠ADE＝∠BCF ‎ ‎ ‎4、已知：如图，△ABC中，AB＝AC，AD是BC边上的高，AE是△BAC的外角平分线，DE∥AB交AE于点E，求证：四边形ADCE是矩形。‎ ‎5、已知：如图，菱形ABCD的对角线AC与BD交于点O，延长BA到点E，使AE＝AB，连结OE、DE，并延长DE交CA的延长线于点F；求证：OE＝DF。‎ ‎6、已知：如图，在正方形ABCD中，F是CD边上的中点，点P在BC上，∠1＝∠2，PE⊥BC交AC于点E，垂足为P。求证：AB＝3PE。‎ ‎ ‎ ‎7、如图，梯形ABCD中，AB∥CD，对角线AC、BD交于点O，∠1＝∠2，AB＝2BO；求证：CD＝3AB ‎8、已知：如图，在△ABC中，∠BCA＝90°，D、E分别是AC、AB的中点，点F在BC延长线上，且∠CDF＝∠A；‎ ‎（1）求证：四边形DECF是平行四边形；‎ ‎（2），四边形EBFD的周长为22，求DE的长。‎ 4‎ ‎（第三套）‎ 一：1、；6、；2、；3、≥2；4、；5、4cm；6、5cm；7、20cm；‎ ‎ 8、‎6cm；9、‎9cm；10、‎8cm；11、7.2；12、，。13、7.5；14、450。‎ 二、DDACA，DBDDB，C 三：1、原式＝‎ ‎ 2、原式＝‎ ‎3、可证：△ADF≌△BCF（SAS）‎ ‎4、提示：证AEDB是平行四边形得AE平行且等于BD，又因为BD＝DC，所以AE平行且等于DC，故ADCE是平行四边形，又因∠ADC＝Rt∠，所以ADCE是矩形。‎ ‎5、菱形ABCDBE∥DC，又∵AB＝CD，AE＝AB。∴∴OE是Rt△FOD斜边上的中线，∴0E＝DF。‎ ‎6、∵△PCE是等腰直角三角形 ‎ ∴PE＝PC ‎ 由△CFP∽△BAP可得；‎ ‎∴ ∴ 即AB＝3PE ‎7、提示；‎ ‎△BAO∽△BDA 梯形ABCD ‎8、①∵EC是Rt△ABC斜边上的中线 ‎ ∴EA＝EC ‎ ∴∠A＝∠ECA 又∵∠A＝∠CDF ‎ ∴∠ECA＝∠CDF ‎ ∴EC∥DF 又∵中位线ED∥BF ‎ ∴DECF是平行四边形 ‎②设BC＝，则AB＝，BE＝EC＝DF＝，ED＝CF＝，由周长为22可得＝2，故DE＝3。‎ 4‎