华师版数学八年级下册同步练习课件-期末复习4矩形、菱形与正方形

华师版数学八年级下册同步练习课件-期末复习4矩形、菱形与正方形

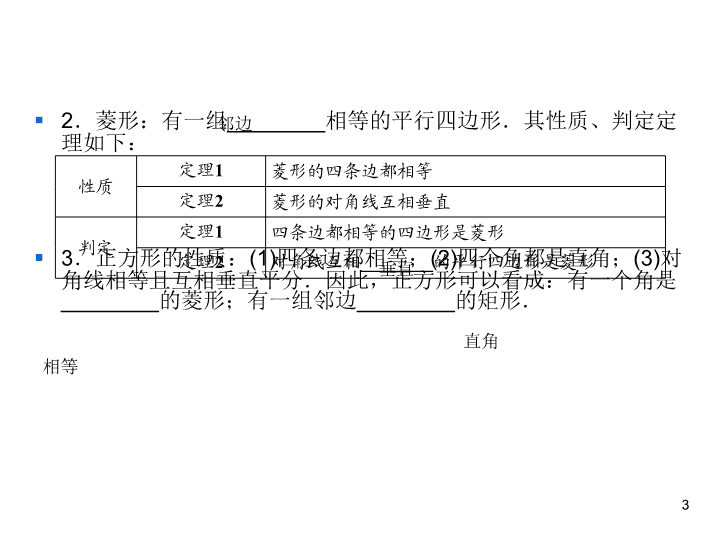
期末复习 期末复习4　矩形、菱形与正方形 § 1．矩形：有一个角是________的平行四边形．其性质、判定定理如下： 2 性质 定理1 矩形的四个角都是直角 定理2 矩形的对角线相等 判定 定理1 有三个角是______角的四边形是矩形 定理2 对角线________的平行四边形是矩形 直角　　 直　 相等　 § 2．菱形：有一组________相等的平行四边形．其性质、判定定 理如下： § 3．正方形的性质：(1)四条边都相等；(2)四个角都是直角；(3)对 角线相等且互相垂直平分．因此，正方形可以看成：有一个角是 ________的菱形；有一组邻边________的矩形． 3 性质 定理1 菱形的四条边都相等 定理2 菱形的对角线互相垂直 判定 定理1 四条边都相等的四边形是菱形 定理2 对角线互相________的平行四边形是菱形 邻边　 垂直　 直角　 相等　 § ★集训1　矩形的性质与判定 § 1．如图，在矩形ABCD中，AB＝3，对角线 AC、BD相交于点O，AE垂直平分OB于点E， 则AD的长为_______. § 2．如图，在矩形ABCD中，对角线AC、BD相交于点O，EF是OA的中垂线，分别交AD、 OA于点E、F.若AB＝6 cm，BC＝8 cm，则 △DEO的周长为______cm. 4 13　 § 3．如图1，四边形ABCD是平行四边形，BD 是它的一条对角线，过顶点A、C分别作 AM⊥BD，CN⊥BD，点M、N为垂足． § (1)求证：AM＝CN； § (2)如图2，在对角线DB的延长线及反向延长 线上分别取点E、F，使BE＝DF，连结AE、 CE、CF、AF，试探究：当EF满足什么条件 时，四边形AECF是矩形？并加以证明． 5 6 7 § ★集训2　菱形的性质与判定 § 4．如图，△ABC中，DE∥BC，EF∥AB， 要判定四边形DBFE是菱形，还需要添加的 条件是(　　) § A．AB＝AC § B．AD＝BD § C．BE⊥AC § D．BE平分∠ABC 8 D 　 § 6．如图，在菱形ABCD中，∠DAB＝60°， DF⊥AB于点E，且DF＝DC，连结FC，则 ∠DCF＝______°. 9 A 　 45　　 § 7．如图，在四边形ABCD中，AD∥BC，AB ＝BC，对角线AC、BD交于点O，BD平分 ∠ABC，过点D作DE⊥BC的延长线于点E， 连结OE.求证：四边形ABCD是菱形． § 证明：∵AD∥BC，∴∠ADB＝ ∠CBD.∵BD平分∠ABC，∴∠ABD＝ ∠CBD，∴∠ADB＝∠ABD，∴AD＝ AB.∵AB＝BC，∴AD＝BC，∴四边形 ABCD是平行四边形．又∵AB＝BC，∴四边 形ABCD是菱形． 10 § ★集训3　正方形的性质与判定 § 8．如图，已知正方形ABCD，点E在边DC上， DE＝4，EC＝2，则AE的长为_______. 11 § 9．【浙江台州中考】如图，在正方形ABCD中，AB＝ 3，点E、F分别在CD、AD上，CE＝DF，BE、CF相 交于点G.若图中阴影部分的面积与正方形ABCD的面 积之比为2∶ 3，则△BCG的周长为_________. 12 § 10．如图，点E是正方形ABCD对角线AC上 一点，EF⊥AB，EG⊥BC，垂足分别为点F、 G，若正方形ABCD的周长是40 cm. § (1)求证：四边形BFEG是矩形； § (2)求四边形BFEG的周长； § (3)当AF的长为多少时，四边形BFEG是正方 形？ 13 § (1)证明：∵四边形ABCD为正方形， ∴AB⊥BC，∠B＝90°.∵EF⊥AB， EG⊥BC，∴∠BGE＝∠BFE＝∠B＝90°， ∴四边形BFEG是矩形．　(2)解：∵正方形 ABCD的周长是40 cm，∴AB＝40÷4＝ 10(cm)．由题易知，△AEF为等腰直角三角 形，∴AF＝EF，∴四边形BFEG的周长为 2(EF＋BF)＝2(AF＋BF)＝20 cm. § (3)解：若要四边形BFEG是正方形，只需EF ＝BF.∵AF＝EF，AB＝10 cm，∴当AF＝5 cm时，四边形BFEG是正方形． 14 § 一、选择题(每小题4分，共32分) § 1．矩形、菱形、正方形都一定具有的性质是 (　　) § A．邻边相等 B．四个角都是直角 § C．对角线相等 D．对角线互相平分 § 2．下列说法错误的是(　　) § A．对角线互相垂直的四边形是菱形 § B．对角线互相垂直平分且相等的四边形是 正方形 § C．对角线相等的平行四边形是矩形 § D．一组对边平行，一组对角相等的四边形 是平行四边形 15 D 　 A 　 § 3．如图，在矩形ABCD中，对角线AC、BD交于点O，下列说法 错误的是 § (　　) § A．AB∥DC B．AC＝BD § C．AC⊥BD D．OA＝OB § 4．在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E、F分 别为BC、CD的中点，则∠EAF等于(　　) § A．75° B．60° § C．45° D．30° 16 C 　 B 　 17 C 　 C 　 18 C 　 19 D 　 § 二、填空题(每小题5分，共20分) § 9．已知一个菱形的两条对角线的长分别为 10和24，则这个菱形的周长为______. § 10．【湖北武汉中考】以正方形ABCD的边 AD作等边△ADE，则∠BEC的度数是 _______________. 20 52　 30°或150°　 11．如图，矩形ABCD的对角线BD的中点为O，过点O 作OE⊥BC于点E，连结OA，已知AB＝5，BC＝12，则四边形 ABEO的周长为______.20　 § 三、解答题(共48分) § 13．(12分)已知：如图，在矩形ABCD中， 对角线AC与BD相交于点O，过点C、D分别 作BD、AC的平行线，两线相交于点P. § (1)求证：四边形OCPD是菱形； § (2)当矩形ABCD的边AD、DC满足什么关系 时，菱形OCPD是正方形？请说明理由． 21 22 § 14．(16分)如图，菱形ABCD的 对角线交于点O，BE∥AC， AE∥BD，EO与AB交于点F. § (1)求证：EO＝DC； § (2)若菱形ABCD的边长为10， ∠EBA＝60°，求菱形ABCD的 面积． 23 § 15．(20分)已知：正方形ABCD中，∠MAN ＝45°，∠MAN绕点A顺时针旋转，它的两 边分别交CB、DC(或它们的延长线)于点M、 N，AH⊥MN于点H. § (1)如图1，当∠MAN绕点A旋转到BM＝DN 时，请你直接写出AH与AB的数量关系： __________； § (2)如图2，当∠MAN绕点A旋转到BM≠DN时， (1)中发现的AH与AB的数量关系还成立吗？ 如果不成立请写出理由；如果成立请证明； § (3)如图3，已知∠MAN＝45°，AH⊥MN于 点H，且MH＝2，AH＝6，求NH的长．(可利 用(2)得到的结论) 24 AH＝AB　 25 §(3)解：如图，分别沿AM、AN翻折△AMH 和△ANH，得到△ABM和△AND，则BM＝2， AB＝AD＝AH＝6，DN＝NH，∠B＝∠D＝ ∠BAD＝90°.分别延长BM和DN交于点C， 得正方形ABCD.设NH＝x，则MC＝4，NC＝ 6－x.在Rt△MCN中，MN2＝MC2＋NC2，即 (x＋2)2＝42＋(6－x)2，解得x＝3.∴NH＝3. 26