- 2021-11-01 发布 |
- 37.5 KB |
- 27页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上数学课件八年级上册数学课件《画轴对称图形》 人教新课标 (7)_人教新课标
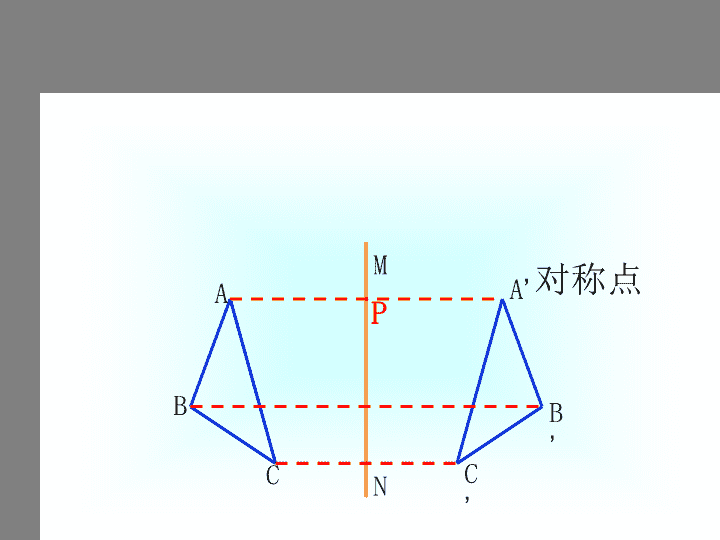
画轴对称图形 对称点 B A C M N A’ B’ C’ P 我们可由一个图形得到与它 成轴对称的另一个图形,重 复此过程,可得到美丽的图 案 由一个平面图形得到它 的轴对称图形的过程叫 做轴对称变换 . . . . 对称轴方向和位置发生变化时, 得到的图形的方向和位置也会发生 变化。 来吧!动动脑筋动动手 . . . . . . 探究轴对称变换 性质: 1、由一个平面图形可以得到它关于一条 直线L成轴对称的图形,这个图形与原图形的形 状、大小完全一样。 2、新图形上的每一点,都是原图形上的某 一点关于直线L的对称点。 3、连接任意一对对应点的线段被对称轴 垂直平分。 · ·· · · ·A A′ B B′ C C′ ┓ ┓ ┓ 讨论: 如果有一个图形和一条直线, 如何作出与这个图形关于这条直线 对称的图形呢? 已知直线 和一个点A,作出与 点A关于直线 对称的图形点A′。 A A' ∴ 点A′即为所求 M l ┓ O 基础一 l l A B 已知直线L和线段AB,作出与线段AB关于直 线 L对称的图形线段A′B′。 A' B' l M N ┓ ┓ O P 基础二 ∴线段A′B′即为所求 A B C 例1 如图,已知△ABC和直线l,作出与 △ABC关于直线l对称的图形。 ┐ ┐ ┐l 作法: (1)过点A作直线l的垂 线,垂足为点O,在垂线 上截取OA′=OA,点A′就 是点A关于直线l的对称点 。 (4)连接A′B′、B′C′、C′A′,得 到△A′B′C′即为所求。 O P M (2)过点B作直线l的垂线, 垂足为点P,在垂线上截取 PB′=PB,点B′就是点B关于 直线l的对称点。 (3)过点C作直线l的垂线, 垂足为点M,在垂线上截取 MC′=MC,点C′就是点C关于 直线l的对称点。 我行了:如图,已知△ABC和直线l,作出与 △ABC关于直线l对称的图形。 B A C B A C l B’ C’ B A C A’ B’ ∴△AB’C’即为所求。 作法: 1、分别作出点B、C关于 直线l的对称点B’、C’; 2、连接AB’、B’C’、 C’A。 B C l 作法: 1、分别作出点A、B关于 直线l的对称点A’、B’; 2、连接A’B’、B’C、 CA’。 ∴△A’B’C即为所求。 作已知图形关于已知直线对称的图形的一般步聚: 1、找点 2、画点 3、连线 (确定图形中的一些特殊点); (画出特殊点关于已知直线的对称点); (连接对称点)。 B A C A’ B’ l 练习 1、如图,把下列图形补成关于直线L的 对称图形。 归纳 几何图形都可以看作由点组成,只要 作出这些点关于对称轴的对应点,再 连接对应点,就可以得到原图形的轴 对称图形 对于一些由直线、线段或射线组成的图 形只要作出图形中的一些特殊点的对称 点,再连接对称点,就可以得到原图形 的轴对称图形 l 如图给出了一个图案的一 半,其中的虚线 l 是这个图 案的对称轴。 整个图案是个什么形状? 请准确地画出它的另一半。 巩固 提高 B A C D EF G H 实际图形和印章中的像可以 看成上图那样的成轴对称关系。 轴对称变换后的像原来的像 轴对称变换前后的 图形是一对“好朋友” ,在一次活动中他们走散了,请同学们帮助他 们找回自己的“好朋友”。 用两个圆、两个三角形、两条平行线段可以 构造出许多独特而有意义的轴对称图形(如下 图),请你也仿照构思一个图案,别忘了加上 一两句贴切的解说词哦. 活动 两盏电灯 图片欣赏 图片欣赏 图片欣赏 图片欣赏 图片欣赏 (1)轴对称变换的定义 (2)轴对称变换的性质 (4)轴对称变换在生活中的应用 (3)利用轴对称变换的性质作图 再 见查看更多