八年级下数学课件：19-3 课题学习 选择方案 （共16张PPT）_人教新课标

八年级下数学课件：19-3 课题学习 选择方案 （共16张PPT）_人教新课标

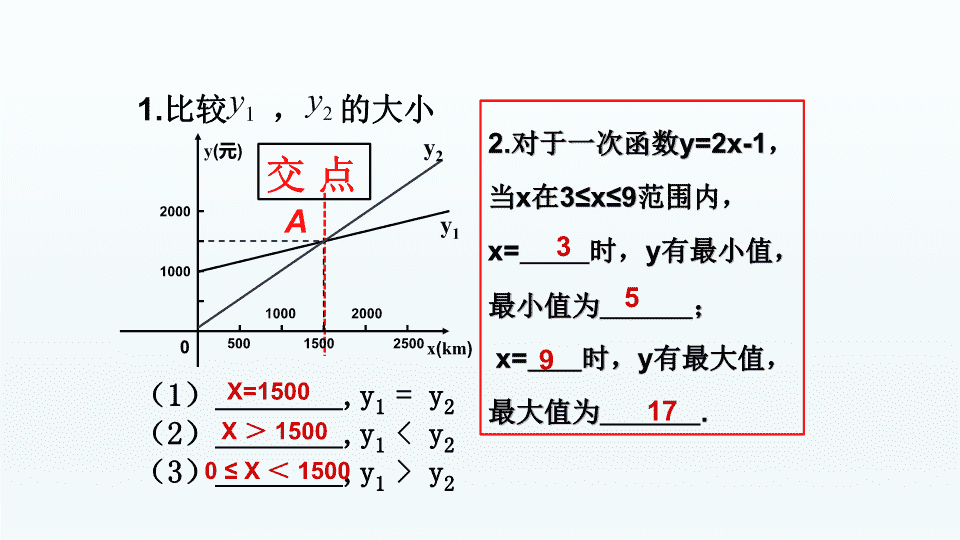
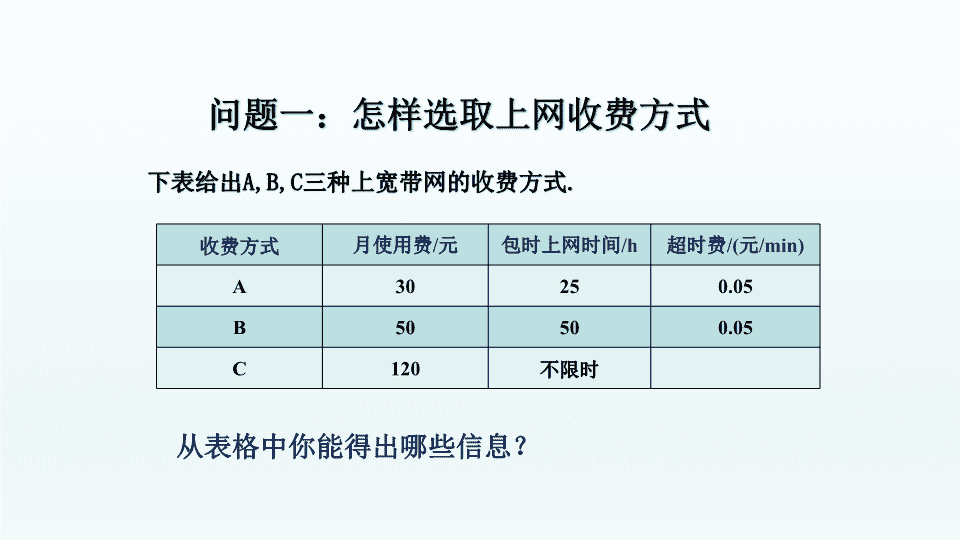
课题学习 1y 2y1.比较 ， 的大小 3 5 9 17 交 点 （1） ,y1 = y2 （2） ,y1 < y2 （3） ,y1 > y2 我回顾 1000 2000 500 1500 1000 2000 2500 x(km) y(元) 0 y1 y2 X=1500 X ＞ 1500 0 ≤ X ＜ 1500 收费方式 月使用费/元 包时上网时间/h 超时费/(元/min) A 30 25 0.05 B 50 50 0.05 C 120 不限时 我探究 从表格中你能得出哪些信息？ 收费方式 月使用费/元 包时上网时间/h 超时费/(元/min) A 30 25 0.05 B 50 50 0.05 C 120 不限时 1.哪种方式上网费会变化？哪种不变？ A、B会变化，C不变 2. ①方式C上网费是多少钱？ 120元 ②在A、B两种方式中，上网费由哪些部分组成？ 上网费=月使用费 上网费=月使用费+超时费 3.影响方式A、B上网费用的因素是什么？ 上网时间 我探究 收费方式 月使用费/元 包时上网时间/h 超时费/(元/min) A 30 25 0.05 B 50 50 0.05 C 120 不限时 我探究 收费方式 月使用费/元 包时上网时间/h 超时费/(元/min) A 30 25 0.05 合起来表示为： 1 30, (0 25) 3 45. ( 25) x y x x     ＞ 我探究 收费方式 月使用费/元 包时上网时 间/h 超时费/(元 /min) A 30 25 0.05 B 50 50 0.05 C 120 不限时 2 50, (0 50) 3 100. ( ) x y x x     ＞50 我探究 收费方式 月使用费/元 包时上网时 间/h 超时费/(元 /min) A 30 25 0.05 B 50 50 0.05 C 120 不限时 2 50, (0 50) 3 100. ( ) x y x x     ＞50 我探究 1 30, (0 25) 3 45. ( 25) x y x x     ＞ 提问：你能在同一直角坐标系中画出它们的图象吗? 120 1203 y 当上网时间_________时， 选择方式A最省钱. 交 点 ● ● 当上网时间为 时， 选择方式A、B费用一样。 23 1 3 X  当上网时间为 时， 选择方式B、C费用一样。 17 3 3 X  23 1 3 17 3 3 我反思 解决实际问题最优方案的基本策略： 1.分析问题： ①明确问题； ②分析数量关系，建立函数模型 2.解决问题： 数：方程、不等式 形：图象 作图 找交点（即相等情况） 根据图象选择最优方案 1.如图所示， l1反映了某公司产品的销售收入与销售量的关系， l2反映了该公司产品的销售成本与销售量的关系，根据图象判 断该公司盈利时的销售量是（ ） A．小于4件 B．大于4件 C．等于4件 D．大于或者等于4件 我评价 B 2.某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡： ① 金卡售价600元/张，每次凭卡不再收费； ② 银卡售价150元/张，每次凭卡另收10元。 暑期普通票正常出售，两种优惠卡仅限暑期使用，不限次数。 设游 泳x次时，所需总费用为y元。 （1）分别写出选择银卡、普通票消费时，y与x之间的函数关系式； （2）在同一个坐标系中，若三种消费 方式对应的函数图像如图所示，请求 出点A、B、C的坐标； （3）请根据函数图象，直接写出选择 哪种消费方式更合算。 我评价 2.某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡： ① 金卡售价600元/张，每次凭卡不再收费； ② 银卡售价150元/张，每次凭卡另收10元。 暑期普通票正常出售，两种优惠卡仅限暑期使用，不限次数。 设游 泳x次时，所需总费用为y元。 （1）分别写出选择银卡、普通票消费时，y与x之间的函数关系式； 解：（1）根据题意，可知： 银卡：y=10x+150 （x≥0）         普通票：y=20x （x≥0）    我评价 2.某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡： ① 金卡售价600元/张，每次凭卡不再收费； ② 银卡售价150元/张，每次凭卡另收10元。 暑期普通票正常出售，两种优惠卡仅限暑期使用，不限次数。 设游 泳x次时，所需总费用为y元。 （2）在同一个坐标系中，若三种消费方式对应的函数图像如图所示， 请求出点A、B、C的坐标； 我评价 解：（2）根据题意和图象可知： 当x=0时，y=10x+150=150 则点A的坐标是（0，150） 则点B的坐标是（15，300） 当y=600时，600=10x+150=150，解得x=45 则点C的坐标是（45，600） 2.某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡： ① 金卡售价600元/张，每次凭卡不再收费； ② 银卡售价150元/张，每次凭卡另收10元。 暑期普通票正常出售，两种优惠卡仅限暑期使用，不限次数。 设游 泳x次时，所需总费用为y元。 （3）请根据函数图象，直接写出选择哪种消费方式更合算。 我评价 解：（3）根据图象，可知： 当0 ≤ x＜15时，选择购买普通票更合算； 当x=15时，选择购买银卡、普通票的总费 用相同，均比金卡合算； 当15＜x＜45时，选择购买银卡更合算； 当x=45时，选择购买金卡、银卡的总费用 相同，均比普通票合算； 当x＞45时，选择购买金卡更合算 。 1.这节课我学到了什么？ 2.本节课渗透了哪些数学思想？ (建立函数模型、数形结合、分类讨论) 课堂小结 实际问题 函数模型 （函数解析式） 实际问题的解 函数图像 抽象概括 还原说明