八年级上数学课件《实数》 (3)_苏科版

八年级上数学课件《实数》 (3)_苏科版

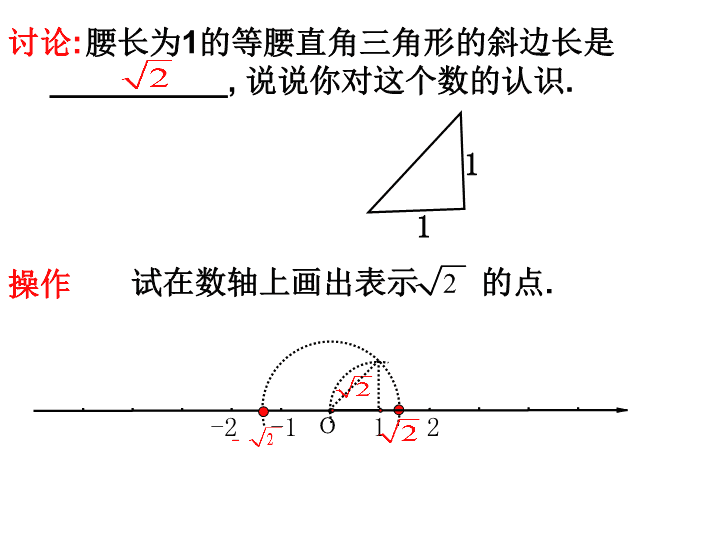
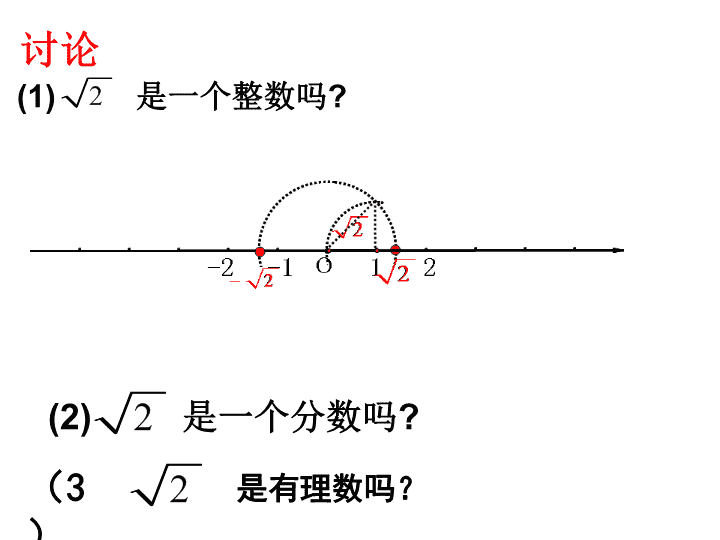
腰长为1的等腰直角三角形的斜边长是 __________, 说说你对这个数的认识. 讨论: 操作 试在数轴上画出表示 的点.2 1o 2-2 -1 1 1 讨论 (1) 是一个整数吗? 2 (2) 是一个分数吗? 2 是有理数吗？2（3） , 2 ,  事实上人们已经证明 是一个无限不循环小数 它的值为 1.4142135623730950488016887242097 结论 2 ,是一个无限不循环小数 1.无理数的概念 无限不循环小数称为无理数. 3 33 , 5 , 2 , 3,0.1010010001..., 2.31456728... .   等都是无理数 圆周率 也是无理数,- 也是无理数. 2 两个条件:①无限小数;②不循环小数 缺一不可 注意 2.实数的概念: 有理数和无理数统称为实数. 即实数可分为有理数和无理数. 实数 有理数 无理数 整数 零 分数 正无理数 负无理数 正整数 负整数 正分数 负分数 有限小数或无 限循环小数 无限不循环小数 实数的分类： 自 然 数 实数 正实数 负实数 正有理数 零 负有理数 正无理数 负无理数 还可如下分类 (4)负实数集合{ …} (3)正实数集合{ …} 例题 把下列各数填人相应的集合内:     3 324 , 9 ,0.6 , 10 , 125 , 27 , , 3 3 16 22, ,0.01001000100001 . 49 7 (1) : ; (2) : ;        有理数集合 无理数集合 24 , 3 0.6,  3 125, 16 22, , 49 7  3 9 , 10 , 27 , , 3  0.01001000100001 . 24 , 3 27 , , 3  0.6, 10,  22 ,0.01001000100001 . 7  3 9, 3 125, 1 6 , 4 9  练习1:判断： （1）无理数都是无限小数 （2）无限小数都是无理数 （3）两个无理数的和一定是无理数 (6)整数和分数统称为有理数 ) √ × × × × √ 2.把下列各数分别填入相应的集合中： 整数集合 分数集合 有理数集合 无理数集合 ··· ··· ··· ··· 讨论 有理数都可以用数轴上的点来表示， 反过 来，数轴上的点是否都表示有理 数？ 每一个实数都可以用数轴上的一个 点来表示，；反之，数轴上的每一个点 都表示一个实数，实数与数轴上的点 是一一对应的。 练一练 1.和数轴上的点一一对应的数集是 ( ) A. 有理数集 B. 无理数集 C. 整数集 D. 实数集 2.在实数 中整数有_______________________________; 有理数有______________________________; 无理数有_____________________________. 3 3 322 1, , , 2 ,0.3 , 9 , 8 ,0 ,0.30330333 7 3     D 3 8 ,0 ,0.30330333 22 1, , 7 3  0.3  3, 2 3 9 3.下列语句中正确的是 ( ) A.带根号的数都是无理数 B.不带根号的数都是有理数 C.无理数一定是无限不循环小数 D.无限小数一定是无理数 C 4.(1)在数轴上找出表示 的点. (2)在数轴上找出表示 的点. 10 5 1..无理数的常见形式: ①π是无理数; ② 带根号且开方开不尽的数; ③0.1010010 001… 2.实数与数轴上的点是一一对应的 实数 有理数 无理数 整数 零 分数 正无理数 负无理数 正整数 负整数 正分数 负分数 有限小数或无 限循环小数 无限不循环小数 3.实数的分类： 自 然 数 实数 正实数 负实数 正有理数 零 负有理数 正无理数 负无理数 还可如下分类 会将一个数进行分类是重点 能将一个无理数在数轴上表示出来是难点 • 1.判断正误，若不对，请说明理由，并加以 改正。 • （1）无理数都是无限小数。 （2）带根号 的数不一定是无理数。 • （3）无限小数都是无理数。 （4）数轴上 的点表示有理数。 • （5）不带根号的数一定是有理数。 • 2、数 、 、 中，无理数有（ ）． • （A）0个 （B）1个 （C）2个 （D） 3个 • 3.（1）把下列各数填入相应的集合内：-7， 0.32， ． • 有理数集合：{ …}； • 无理数集合：{ …}． 1 4 3 2 2  1 3 8 3 216 2  • 4、把下列各数分别填入相应的集合内。 • • • 0.3737737773……（相邻两个3之间7的个 数逐次增加1） • 正有理数： • 负有理数： • 有理数： • 无理数： 3 2 4 1 7  2 5  2 3 20 5 3 8 9 4