- 2021-10-27 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
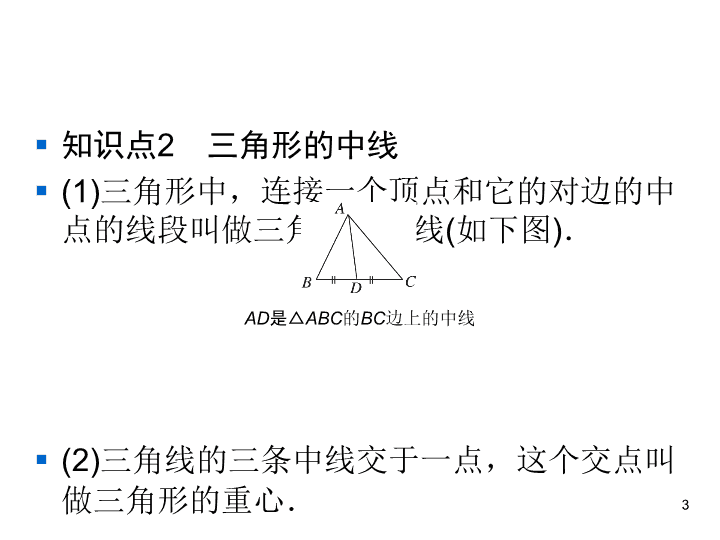
人教版八年级上册数学同步练习课件-第11章-11三角形的高、中线与角平分线(第二课时)
第十一章 三角形 11.1 与三角形有关的线段 11.1.2 三角形的高、中线与角平分线(第二课时) § 知识点1 三角形的高 § 从三角形的一个顶点向它的对边所在的直线 作垂线,顶点和垂足之间的线段叫做三角形 的高(如下图). 2 AD是△ABC的BC边上的高 § 知识点2 三角形的中线 § (1)三角形中,连接一个顶点和它的对边的中 点的线段叫做三角形的中线(如下图). § (2)三角线的三条中线交于一点,这个交点叫 做三角形的重心. 3 AD是△ABC的BC边上的中线 § 知识点3 三角形的角平分线 § 三角形的一个内角的平分线与它的对边相交, 这个角的顶点与交点之间的线段叫做三角形 的角平分线(如下图). 4 AD是△ABC的角平分线 § 注意:每个三角形都有三条高、三条中线和 三条角平分线,且它们都是线段;三条中线、 角平分线一定相交,交点分别叫做重心、内 心,且位于三角形的内部,三条高所在的直 线一定相交,交点叫做垂心,交点可以在三 角形的内部、外部或边上. 5 § 1.如图,过△ABC的顶点A,作BC边上的 高,以下作法正确的是( ) 6 A § 2.如图,已知BD是△ABC的中线,则下列 说法正确的是( ) § A.△ABD的面积等于△CBD的面积 § B.△ABD的面积大于△CBD的面积 § C.△ABD的面积小于△CBD的面积 § D.无法确定 § 3.如图,在△ABC中,BD是∠ABC的平分 线,已知∠ABC=80°,则∠DBC= ___________. 7 A 40° § 4.如图,在△ABC中,BD 是角平分线,BE为中线,BF 是高.若AC=12 cm,则AE =_________ cm;若∠ABC =80°,∠A=45°,则 ∠DBF=__________. § 5.如图,在△ABC中,∠C =90°,AC=8,BC=6, AB=10,则AB边上的高为 ___________. 8 6 5° 4.8 § 6.如图,在△ABC中,AD是 角平分线,DE∥AC交AB于点 E,EF∥AD交BC于点F,试问: EF是△BDE的角平分线吗?说 说你的理由. 9 § 7.三条高的交点一定在三角形内部的是( ) § A.任意三角形 B.锐角三角形 § C.直角三角形 D.钝角三角形 § 8.在△ABC中,D是BC上的点,且BD∶ DC =2∶ 1,S△ACD=12,则S△ABC等于( ) § A.30 B.36 § C.72 D.24 10 B B § 9.如图,△ABC的角平分线AD、中线BE相 交于点O,则①AO是△ABE的角平分线; ②BO是△ABD的中线;③DE是△ADC的中 线;④ED是△EBC的角平分线.结论中正确 的有( ) § A.1个 § B.2个 § C.3个 § D.4个 11 B § 10.【2018·四川巴中中考】如图,在 △ABC中,BO、CO分别平分∠ABC、 ∠ACB.若∠BOC=110°,则∠A= ___________. § 解析:∵BO、CO分别平分∠ABC、∠ACB, ∴∠A=180°-(∠ABC+∠ACB)=180° -2(∠OBC+∠OCB)=180°-2(180°- ∠BOC)=180°-2(180°-110°)=40°. 12 40° § 11.如图,A、B、C分别是线段 A1B、B1C、C1A的中点,若 △ABC的面积是1,那么△A1B1C1 的面积是_________. 13 7 解析:连接AB1、BC1、CA1.∵A是线段A1B的中点,∴AB=AA1,∴S△ABC= S△AA1C,S△AA1B1=S△ABB1.∵B是线段B1C的中点,∴BB1=BC,∴S△ABC= S△ABB1,S△BB1C1=S△BCC1.∵C是线段AC1的中点,∴AC=CC1,∴S△ABC= S△BCC1,S△AA1C=S△A1C1C,∴S△ABC=S△AA1C=S△ABB1=S△BCC1= S△BB1C1=S△A1C1C=S△AA1B1=1,∴S△A1B1C1=7S△ABC=7. § 12.如图所示,已知AD、AE分别是△ABC 的高和中线,AB=6 cm,AC=8 cm,BC= 10 cm,∠CAB=90°.试求: § (1)AD的长; § (2)△ABE的面积; § (3)△ACE和△ABE的周长的差. 14 § 13.将一副三角板拼成如图所示的 图形,过点C作CF平分∠DCE, 交DE于点F. § (1)求证:CF∥AB; § (2)求∠DFC的度数. 15 § 14.如图,已知在直角三角形ABC中,∠ABC= 90°,点D沿BC自B向C运动(点D与点B、C不重 合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的 值如何变化?请说明理由. 16 17查看更多