八年级上数学课件《一次函数与二元一次方程》 (7)_苏科版

八年级上数学课件《一次函数与二元一次方程》 (7)_苏科版

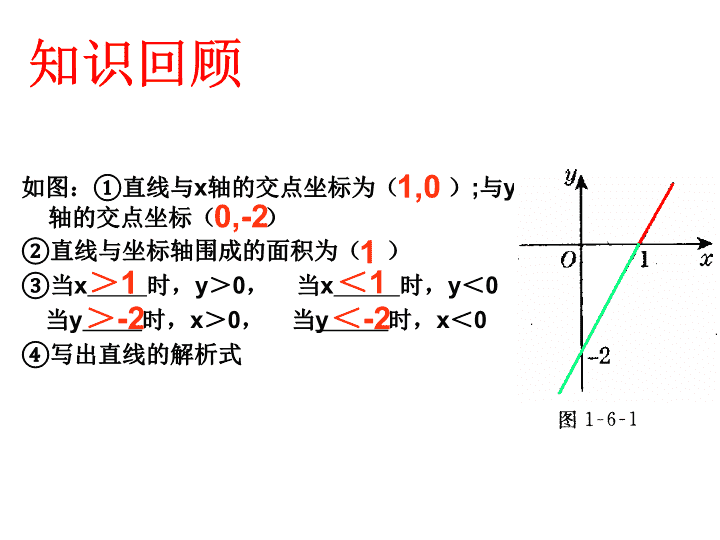
一次函数与二元一次方程 知识回顾 k ﹥o b ﹥o k ﹤ o b ﹥o k ﹥o b ﹤ o k ﹤ o b ﹤ o 一次函数y=kx＋b是过 （0， ）、 （ ，0） 两点的一条直线 ,正比例函数y=kx的图象一定过点 ( 0 ,___), ( 1 ,___). b 0 k b 如图：①直线与x轴的交点坐标为（　　）;与y 轴的交点坐标（　　） ②直线与坐标轴围成的面积为（　） ③当x 时，y＞0， 当x 时，y＜0 　当y 时，x＞0， 当y 时，x＜0 ④写出直线的解析式 1,0 0,-2 1 ＞1 ＜1 ＞-2 ＜-2 知识回顾 1.二元一次方程2x－y－3=0可以写成一 次函数y=2x－3的形式；反过来，一次函数 y=2x－3可以写成二元一次方程2x－y－3=0 的形式。从形式上看，你知道是通过什么 方法变形得到的？ 从形式上看，通过移项，二元一次方程 可以化为一次函数的形式，一次函数可以 化成二元一次方程的形式。 2.把下列二元一次方程写成y=kx＋b的形式： （1）3x＋y=7 (2) 3x＋4y=13 活动1 1、问题：方程2x-y-3=0的解有多少个？你能写几个 出来吗？ 2、在直角坐标系中分别描出以这些解为坐标的点， 它们在一次函数y=2x-3的图象上吗？ 3、在一次函数y=2x-3的图象上任取一点，它的坐标 适合方程2x-y-3=0吗？ 4、方程2x-y-3=0的解为坐标的所有点组成的图象与一 次函数y=2x-3的图象相同吗？ 活动2 5 、二元一次方程2x-y-3=0的解与一次函数y=2x-3图象 上的点有什么关系？ x y 0 y = 2x-3  5,1   3,0   1,1   1,2  3,3  0,2 3 二元一次方程2x-y-3=0的解 与一次函数y=2x-3图象上的点 有什么关系？ 以二元一次方程2x-y-3=0的 一个解为坐标就是相应一次 函数y=2x-3图象上的点 一次函数y=2x-3的图象上 任一点坐标都是相应方程 2x-y-3=0的一个解 二元一次方程的解与一次函数图象上 的点有什么关系？你认为应如何表述? 一般地,一次函数y=kx＋b图象上任 意一点的坐标都是二元一次方程kx－y ＋b=0 的一个解; 以二元一次方程kx－y＋b=0的解 为坐标的点都在一次函数y=kx＋b的图 象上. 1、方程 x – y = 1 有一个解是 ，则 一次函数 y = x – 1 的图象上必有一个点的 坐标为 。 2、一次函数 y = 2x – 4 的图象上有一个点 的坐标为 ，则方程 2x – y = 4 必有一 个解是 。  2,3 你能得到什么结论?你能说明这一结论的 正确性吗? 一次函数y=2x－3和 y = - x + 3的图象,与相应的 二元一次方程组 的解有关系吗? 问题1：（1）在同一直角坐标系中，两个一次函数y=2x －3和 y = - x + 3的图象的位置有什么关系？有无交点？ 若有，交点坐标 是什么？ （2）你会解二元一次方程组 吗？它的解是什么？      3 032 yx yx 问题2 ： 二元一次方程组 的解与两个一次 函数y=2x－3和 y = - x + 3图象交点的坐标有关系吗？      3 032 yx yx y = - x + 3 的解方程组      3 32 yx yx      1 2 y x  1,2 一般地，如果两个一次函数的图象有一个交点， 那么交点的坐标就是相应的二元一次方程组的解。 3、如图，根据图象写出方程组 的解.      032 032 yx yx x+2y=4 1、 解二元一次方程组 2x-y=3 解：由x+2y=4，得 1 22y x   由2x-y=3,得 y=2x-3 在同一直角坐标系中，画 出这两个函数的图象. x y O P（2，1） 32  xy 22 1  xy ∵ 它们的交点坐标为P（2，1） 利用一次函数的图象 例题 ∴原二元一次方程组的解是      1 2 y x 用一次函数的图象解二元一次方程组的 方法称为二元一次方程组的图象解法。 例题      43 23 xy xy 2.画出函数 的图象，并根据图象回答： （1）当x取什么值时，函数值等于零？ （2）当x取什么值时，函数值大于零？　　　 （3）再画出函数 的图象， 并解方程组 231  xy 432  xy (4)当x取什么值时， 当x取什么值时， 21 yy  21 yy  3、一次函数y=3x-4和 的图象之间有何关系？ 一次函数y=–2x+2，y=–2x+5的图象之间有何关系？ 方程组 有 解。 你能从中“悟”出些什么吗？ 3 14y x   那么，方程组 有 个解。      52 22 xy xy 1 无 (1)如果一次函数的图象平行（无交点），那么二元一次方程组 无解. (2)如果一次函数的图象相交（有一个交点），那么二元一次方 程组有一解. (3)如果一次函数的图象重合（有无数个交点），那么二元一次 方程组有无数个解.      14 3 43 xy xy 例题 我在中国电信公司营业大厅办理上网业务，发现有两 种上网收费方式： 方式A以每分0.1元的价格按上网时间计费; 方式B除收月基费外再以每分0.05元的价格按上网时间 计费。 身边一顾客说他每月上网的费用按方式A计算比按方 式B计算少花3元。 问这位顾客每月上网多长时间？方式B中的月基费是 多少元？ 方式B除收月租费20元外再以每分0.05元的价格按上 网时间计费。 我该如何选择收费方式才能自己更合算? 例题 解法1:设上网时间为x分，若按方式A则收费y=0.1x元; 若按方式B则收费y=0.05x+20元。 在同一直角坐标系中分别画出这两个函数的图象。 解方程组           40 400 ,2005.0 1.0 y x xy xy 得 所以两图象交于点(400，40) 当0≤x<400时，直线y=0.1x在直线y=0.05x+20的下方， 0.1x＜ 0.05x+20，选方式A合算。 当x=400时两者均可。 当400

查看更多