【同步作业】人教版 八年级下册数学19课题学习 选择方案

【同步作业】人教版 八年级下册数学19课题学习 选择方案

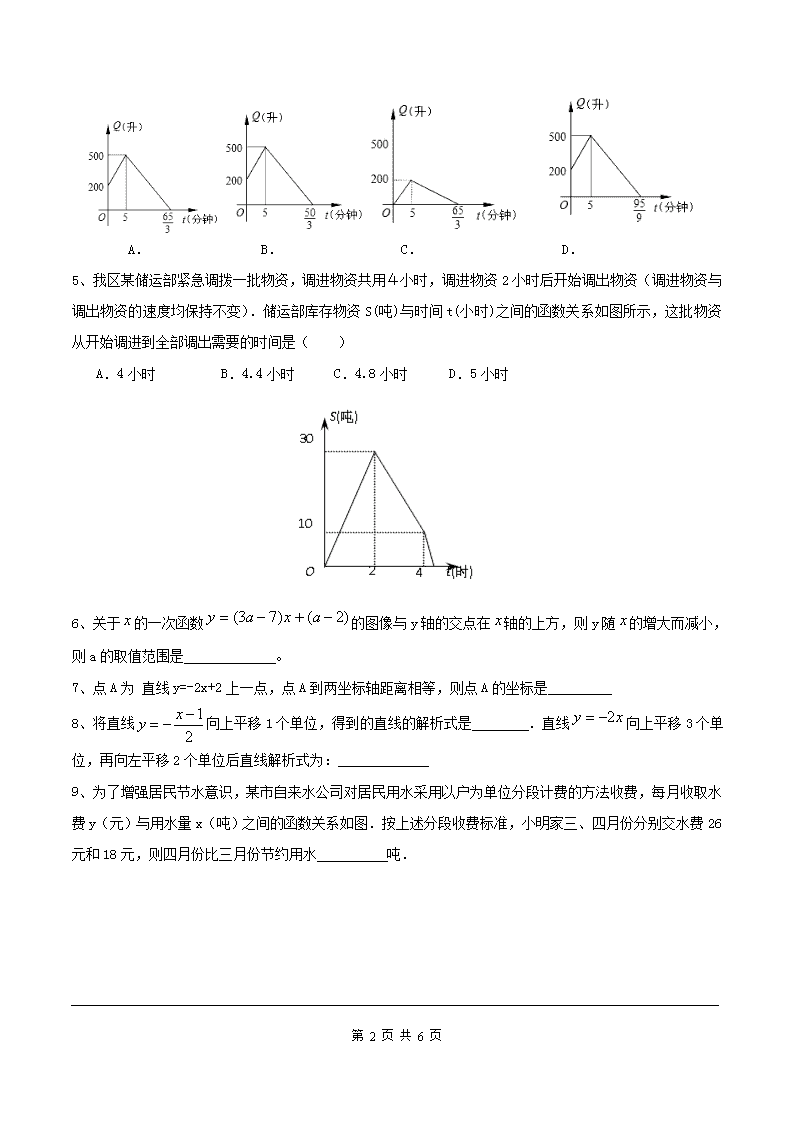
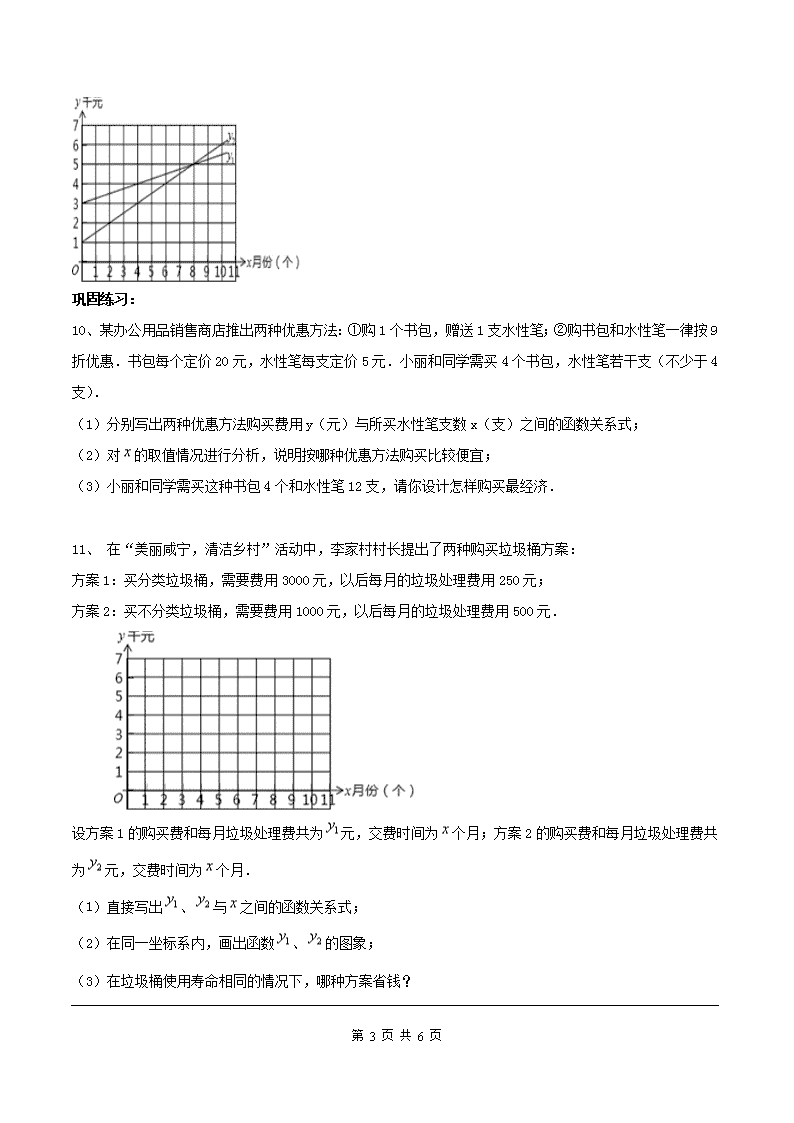
第 1 页 共 6 页 19.3 课题学习 选择方案 基础知识： 1、某地电话拨号入网有两种收费方式：①计时制：0．05 元/分；②包月制：50 元/月．此外，每一种上网 方式都得加收通信费 0．02 元/分．某用户估计一个月上网时间为 20 小时，你认为采用哪种收费方式较为 合算（ ）． A．计时制 B．包月制 C．两种一样 D．不确定 2、小静准备到甲或乙商场购买一些商品，两商场同种商品的标价相同，而各自推出不同的优惠方案：在甲 商场累计购买满一定数额 a 元后，再购买的商品按原价的 90%收费；在乙商场累计购买 50 元商品后，再购 买的商品按原价的 95%收费．若累计购物 x 元，当 x＞a 时，在甲商场需付钱数 yA=0．9x+10，当 x＞50 时， 在乙商场需付钱数为 yB．下列说法：①yB=0．95x+2．5；②a=100；③当累计购物大于 50 元时，选择乙商 场一定优惠些；④当累计购物超过 150 元时，选择甲商场一定优惠些．其中正确的说法是（ ）． A．①②③④ B．①③④ C．①②④ D．①②③ 3、如图是甲、乙两家商店销售同一种产品的销售价 y（元）与销售量 x（件）之间的函数图象．下列说法： ①售 2 件时甲、乙两家售价一样； ②买 1 件时买乙家的合算； ③买 3 件时买甲家的合算； ④买 1 件时，售价约为 3 元， 其中正确的说法有 ．（填序号） 4、如图，有一个装有进、出水管的容器，单位时间内进、出的水量都是 一定的，已知容器的容积为 600L，又知单开进水管 10min 可以把容器注 满，若同时打开进、出水管，20min 可以把满容器的水放完，现已知水池内有水 200L，先打开进水管 5min， 再打开出水管，两管同时开放，直到把容器中的水放完，则正确反映这一过程中容器的水量 Q（L）随时间 t（min）变化的图像是：（ ） 第 2 页 共 6 页 A． B． C． D． 5、我区某储运部紧急调拨一批物资，调进物资共用４小时，调进物资 2 小时后开始调出物资（调进物资与 调出物资的速度均保持不变）．储运部库存物资 S(吨)与时间 t(小时)之间的函数关系如图所示，这批物资 从开始调进到全部调出需要的时间是（ ） A．4 小时 B．4.4 小时 C．4.8 小时 D．5 小时 6、关于 x 的一次函数 )2()73(  axay 的图像与 y 轴的交点在 x 轴的上方，则 y 随 x 的增大而减小， 则 a 的取值范围是 。 7、点 A 为 直线 y=-2x+2 上一点，点 A 到两坐标轴距离相等，则点 A 的坐标是 8、将直线 1 2 xy   向上平移 1 个单位，得到的直线的解析式是 ．直线 xy 2 向上平移 3 个单 位，再向左平移 2 个单位后直线解析式为：_____________ 9、 为了增强居民节水意识，某市自来水公司对居民用水采用以户为单位分段计费的方法收费，每月收取 水费 y（元）与用水量 x（吨）之间的函数关系如图．按上述分段收费标准，小明家三、四月份分别交水费 26 元和 18 元，则四月份比三月份节约用水 吨． 第 3 页 共 6 页 巩固练习： 10、某办公用品销售商店推出两种优惠方法：①购 1 个书包，赠送 1 支水性笔；②购书包和水性笔一律按 9 折优惠．书包每个定价 20 元，水性笔每支定价 5 元．小丽和同学需买 4 个书包，水性笔若干支（不少于 4 支）． （1）分别写出两种优惠方法购买费用 y（元）与所买水性笔支数 x（支）之间的函数关系式； （2）对 的取值情况进行分析，说明按哪种优惠方法购买比较便宜； （3）小丽和同学需买这种书包 4 个和水性笔 12 支，请你设计怎样购买最经济． 11、 在“美丽咸宁，清洁乡村”活动中，李家村村长提出了两种购买垃圾桶方案： 方案 1：买分类垃圾桶，需要费用 3000 元，以后每月的垃圾处理费用 250 元； 方案 2：买不分类垃圾桶，需要费用 1000 元，以后每月的垃圾处理费用 500 元． 设方案 1 的购买费和每月垃圾处理费共为 元，交费时间为 个月；方案 2 的购买费和每月垃圾处理费共 为 元，交费时间为 个月． （1）直接写出 、 与 之间的函数关系式； （2）在同一坐标系内，画出函数 、 的图象； （3）在垃圾桶使用寿命相同的情况下，哪种方案省钱？ 第 4 页 共 6 页 12、某化工厂现有甲种原料 7 吨，乙种原料 5 吨，现计划用这两种原料生产两种不同的化工产品 A 和 B 共 8 吨，已知生产每吨 A，B 产品所需的甲、乙两种原料如下表： 甲种原料 乙种原料 A 产品 0.6 吨 0.8 吨 B 产品 1.1 吨 0.4 吨 销售 A，B 两种产品获得的利润分别为 0.45 万元/吨、0.5 万元/吨．若设化工厂生产 A 产品 x 吨，且销售 这两种产品所获得的总利润为 y 万元． （1）求 y 与 x 的函数关系式，并求出 x 的取值范围； （2）问化工厂生产 A 产品多少吨时，所获得的利润最大？最大利润是多少？ 第 5 页 共 6 页 【参考答案】 1 B 2 C 3 ① ② ③ 4 A 5 C 6 72 3a  7 2 2( , ),(2, 2)3 3  8 2 1y x   9 3 10 （1） ， ； （2）当 x>24 整数时，选择优惠方法②，当 x=24 时，选择优惠方法①，②均可，当 4≤x<24 整 数时，选择优惠方法①；（3）用优惠方法①购买 4 个书包，获赠 4 支水性笔；再用优惠方法②购 买 8 支水性笔． 11 （1）由题意，得 y1=250x+3000，y2=500x+1000； （2）如图所示： （3）由图象可知： ①当使用时间大于 8 个月时，直线 y1 落在直线 y2 的下方，y1＜y2，即方案 1 省钱； ②当使用时间小于 8 个月时，直线 y2 落在直线 y1 的下方，y2＜y1，即方案 2 省钱； ③当使用时间等于 8 个月时，y1=y2，即方案 1 与方案 2 一样省钱； 12 （1）据题意得：y=0.45x+（8-x）×0.5=-0.05x+4 又生产两种产品所需的甲种原料为：0.6x+1.1×（8-x），所需的乙种原料为：0.8x+0.4×（8-x） 则可得不等式组      5)8(4.08.0 7)8(1.16.0 xx xx 解之得 3.6≤x≤4.5 （2）因为函数关系式 y=-0.05x+4 中的 k=-0.05＜0，所以 y 随 x 的增大而减小．则由（1）可知 第 6 页 共 6 页 当 x=3.6 时，y 取最大值，且为 3.82 万元． 答：化工厂生产 A 产品 3.6 吨时，所获得的利润最大，最大利润是 3.82 万元.