华师版数学八年级下册同步练习课件-第19章-19矩 形

华师版数学八年级下册同步练习课件-第19章-19矩 形

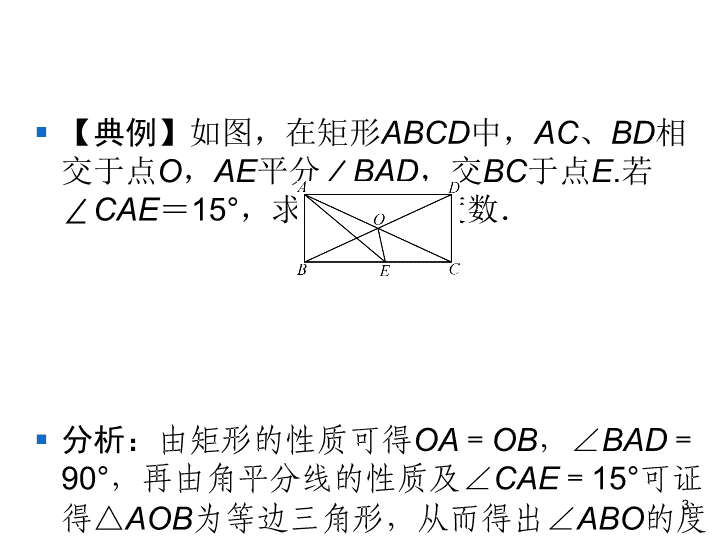
第19章　矩形、菱形与正方形 19.1　矩　形 1　矩形的性质(第一课时) § 知识点1　矩形的定义 § 有一个角是直角的平行四边形叫做矩形． § 知识点2　矩形的性质 § 矩形的性质定理1：矩形的四个角都是直角． § 矩形的性质定理2：矩形的对角线相等． § 核心提示：(1)矩形的四个角都是直角，因此常把与矩形有关的问 题转化到直角三角形中，利用勾股定理解决；(2)矩形的对角线互 相平分且相等，因此矩形的两条对角线把矩形分成四个等腰三角 形，相对的两个三角形全等． 2 § 【典例】如图，在矩形ABCD中，AC、BD相 交于点O，AE平分∠BAD，交BC于点E.若 ∠CAE＝15°，求∠OBE的度数． § 分析：由矩形的性质可得OA＝OB，∠BAD ＝90°，再由角平分线的性质及∠CAE＝ 15°可证得△AOB为等边三角形，从而得出 ∠ABO的度数，进而求出∠OBE的度数． 3 4 5 B 　 B 　 § 3．如图，在矩形ABCD中，对角线AC、BD交于点O，以下说法 错误的是 § (　　) § A．∠ABC＝90° B．AC＝BD § C．OA＝OB D．OA＝AD § 4．如图，在矩形ABCD中，AB＝8，AD＝6，过点D作直线 m∥AC，点E、F是直线m上两个动点，在运动过程中EF∥AC且 EF＝AC，则四边形ACFE的面积是 § (　　) § A．48 B．40 § C．24 D．30 6 D 　 A 　 § 5．如图，在矩形ABCD中，AD＝6，AB＝3， AE平分∠BAD交BC边于点E，则线段EC的 长度为(　　) § A．2 § B．3 § C．4 § D．6 § 6．如图，在矩形ABCD中，∠ABC的平分线 交AD于点E，连结CE.若BC＝7，AE＝4，则 CE＝_____. 7 B 　 5　 § 7．如图，在矩形ABCD中，对角线AC、BD 交于点O，已知∠AOB＝60°，AC＝16，则 图中长度为8的线段有_____条． 8 6　 § 8．【2019·福建中考】如图，点E、F分别 是矩形ABCD的边AB、CD上的一点，且DF ＝BE.求证：AF＝CE. 9 § 9．【浙江杭州中考】如图，已知点P是矩形 ABCD内一点(不含边界)，设∠PAD＝θ1， ∠PBA＝θ2，∠PCB＝θ3，∠PDC＝θ4，若 ∠APB＝80°，∠CPD＝50°，则(　　) § A．(θ1＋θ4)－(θ2＋θ3)＝30° § B．(θ2＋θ4)－(θ1＋θ3)＝40° § C．(θ1＋θ2)－(θ3＋θ4)＝70° § D．(θ1＋θ2)＋(θ3＋θ4)＝180° 10 A 　 11 B 　 § 11．如图，在矩形ABCD中，AD＝4，点P是 直线AD上一动点，若满足△PBC是等腰三角 形的点P有且只有3个，则AB的长为 __________. 12 13 图2 § 12．矩形ABCD中，E、F分别是 AD、BC的中点，CE、AF分别交 BD于G、H两点．求证： § (1)四边形AFCE是平行四边形； § (2)EG＝FH. 14 15 § 13．如图，在矩形ABCD中，连结对角线AC、 BD，将△ABC沿BC方向平移，使点B移到点 C，得到△DCE. § (1)求证：△ACD≌ △EDC； § (2)请探究△BDE的形状，并说明理由． 16 § 14．已知矩形ABCO中，AB＝8，BC＝4， 以点O为原点，OA与OC所在直线分别为y轴 和x轴建立直角坐标系，点B在第一象限． § (1)根据题意，画出图形，并写出点A和点B的 坐标； § (2)若点P从点C出发，以2个单位/秒的速度向 CO方向移动(不超过点O)，点Q从原点O出发， 以1个单位/秒的速度向OA方向移动(不超过点 A)，设P、Q两点同时出发，在它们移动过程 中，四边形OPBQ的面积是否发生变化？若 不变，求其值；若变化，求变化范围． 17 18