华师版数学八年级下册同步练习课件-第18章-18平行四边形的判定

华师版数学八年级下册同步练习课件-第18章-18平行四边形的判定

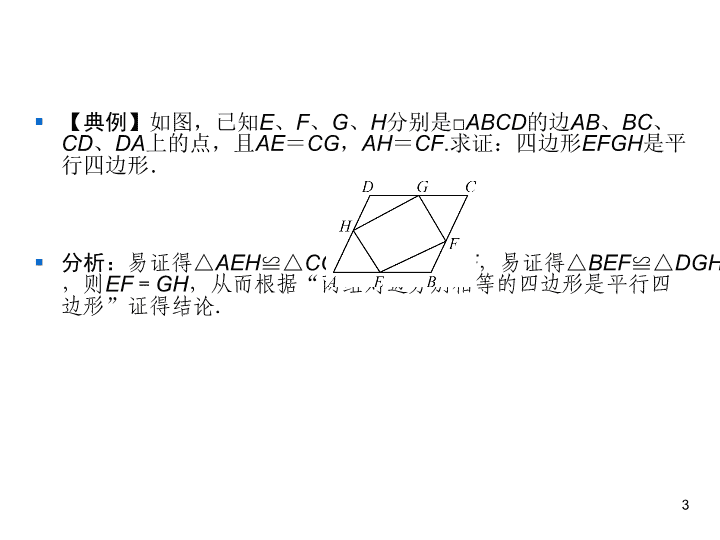
第18章　平行四边形 18.2　平行四边形的判定 第一课时　平行四边形的判定定理1、2 § 知识点1　利用定义进行判定 § 两组对边分别平行的四边形是平行四边形． § 核心提示：两组对边分别平行既是平行四边 形的性质，又是平行四边形的一种判定方法， 它是从平行四边形两组对边的位置关系来判 定的，是其他判定方法的基础． § 知识点2　判定定理1 § 两组对边分别相等的四边形是平行四边形． § 核心提示：此判定定理是通过两组对边的数 量关系进行判定的． 2 § 【典例】如图，已知E、F、G、H分别是□ABCD的边AB、BC、 CD、DA上的点，且AE＝CG，AH＝CF.求证：四边形EFGH是平 行四边形． § 分析：易证得△AEH≌△CGF，则EH＝GF，易证得 △BEF≌△DGH，则EF＝GH，从而根据“两组对边分别相等的 四边形是平行四边形”证得结论． 3 § 证明：在平行四边形ABCD中，∠A＝∠C. § 又∵AE＝CG，AH＝CF， § ∴△AEH≌△CGF， § ∴EH＝GF. § 在平行四边形ABCD中，AB＝CD，AD＝BC， ∠B＝∠D， § 而AE＝CG，AH＝CF， § ∴AB－AE＝CD－CG，AD－AH＝BC－CF， § 即BE＝DG，BF＝DH， § ∴△BEF≌△DGH， § ∴EF＝GH， § ∴四边形EFGH是平行四边形． 4 § 知识点3　判定定理2 § 一组对边平行且相等的四边形是平行四边 形． § 注意：若四边形的一组对边平行，另一组对 边相等，则这个四边形不一定是平行四边形， 它可能是两腰相等的梯形． 5 § 1．下面给出了四边形ABCD中∠A、∠B、 ∠C、∠D的度数之比，其中能判定四边形 ABCD是平行四边形的是(　　) § A．1∶ 2∶ 3∶ 4 B．2∶ 2∶ 3∶ 3 § C．2∶ 3∶ 3∶ 2 D．2∶ 3∶ 2∶ 3 § 2．如图，在平行四边形ABCD中，EF∥AD， HN∥AB，则图中的平行四边形的个数是(　 　) § A．12 B．9 § C．7 D．5 6 D 　 B 　 § 3．如图，在四边形ABCD中，AB＝CD，BC ＝AD，若∠A＝120°，则∠C＝_________. § 4．【2019·黑龙江鸡西中考】如图，在四边 形ABCD中，AD＝BC，在不添加任何辅助线 的情况下加一个条件 ______________________，使四边形 ABCD是平行四边形． 7 120°　 AD∥BC(答案不唯一)　 § 5．【湖南岳阳中考】如图，在平行四边形 ABCD中，AE＝CF，求证：四边形BFDE是 平行四边形． § 证明：∵四边形ABCD是平行四边形， ∴AB∥CD且AB＝CD.又∵AE＝CF，∴BE ＝DF，∴BE∥DF且BE＝DF，∴四边形 BFDE是平行四边形． 8 § 6．如图，点B、E、C、F在一条 直线上，已知AB∥DE，AC∥DF， BE＝CF，连结AD.求证：四边形 ABED是平行四边形． 9 § 7．如图，已知凸五边形ABCDE的边长均相 等，且∠DBE＝∠ABE＋∠CBD，AC＝1， 则BD必定满足(　　) § A．BD＜2 § B．BD＝2 § C．BD＞2 § D．以上情况均有可能 10 A　 § 8．如图，E是□ABCD边AD延长线上一点， 连结BE、CE、BD，BE交CD于点F.添加以 下条件，不能判定四边形BCED为平行四边 形的是(　　) § A．∠ABD＝∠DCE § B．DF＝CF § C．∠AEB＝∠BCD § D．∠AEC＝∠CBD 11 C 　 § 9．如图，△APB中，AB＝2，∠APB＝90°， 在AB的同侧作正△ABD、正△APE和正 △BPC，则四边形PCDE面积的最大值是 _____. 12 1　 13 § 10．如图，在四边形ABCD中，AD∥BC， AD＝5，BC＝18，E是BC的中点．点P以每 秒1个单位长度的速度从点A出发，沿AD向 点D运动；点Q同时以每秒3个单位长度的速 度从点C出发，沿CB向点B运动，点P停止运 动时，点Q也随之停止运动．当运动时间t秒 时，以点P、Q、E、D为顶点的四边形是平 行四边形，则t的值为__________. 14 2或3.5　 § 11．【2019·广西柳州中考】平行四边形的 其中一个判定定理是：两组对边分别相等的 四边形是平行四边形．请你证明这个判定定 理． § 已知：如图，在四边形ABCD中，AB＝CD， AD＝BC. § 求证：四边形ABCD是平行四边形． 15 § 12．【2019·辽宁本溪中考】如图，在四边 形ABCD中，AB∥CD，AD⊥CD，∠B＝ 45°，延长CD到点E，使DE＝DA，连结AE. § (1)求证：AE＝BC； § (2)若AB＝3，CD＝1，求四边形ABCE的面 积． 16 ( 1 )证明：∵A B∥C D，∠B＝45°，∴∠C＋∠B＝180°，∴∠C＝ 135°.∵DE＝DA，AD⊥CD，∴∠E＝45°，∴∠E＋∠C＝180°，∴AE∥BC.又 ∵AB∥CD，∴四边形ABCE是平行四边形，∴AE＝BC.　(2)解：∵四边形ABCE是 平行四边形，∴AB＝CE＝3，∴AD＝DE＝CE－CD＝2，∴四边形ABCE的面积为 CE·AD＝3×2＝6. § 13．如图，将□ABCD沿过点A的直线l折叠， 使点D落到AB边上的点D′处，折痕l交CD边 于点E，连结BE. § (1)求证：四边形BCED′是平行四边形； § (2)若BE平分∠ABC，求证：AB2＝AE2＋ BE2. 17 § 证明：(1)∵将□ABCD沿过点A的直线l折叠， 使点D落到AB边上的点D′处，∴∠DAE＝ ∠D′AE，∠DEA＝∠D′EA，∠D＝ ∠AD′E.∵DE∥AD′，∴∠DEA＝∠D′AE， ∴∠DAE＝∠D′AE＝∠DEA＝∠D′EA， ∴∠DAD′＝∠DED′，∴四边形DAD′E是平行 四边形，∴DE＝AD′.∵四边形ABCD是平行 四边形，∴AB∥DC，AB＝DC，∴CE∥D′B， CE＝D′B，∴四边形BCED′是平行四边形． § (2)∵BE平分∠ABC，∴∠CBE＝ ∠EBA.∵AD∥BC，∴∠DAB＋∠CBA＝ 180°.∵∠DAE＝∠EAB，∴∠EAB＋ ∠EBA＝90°，∴∠AEB＝90°，∴AB2＝ AE2＋BE2. 18