八年级上册数学等腰三角形测试题

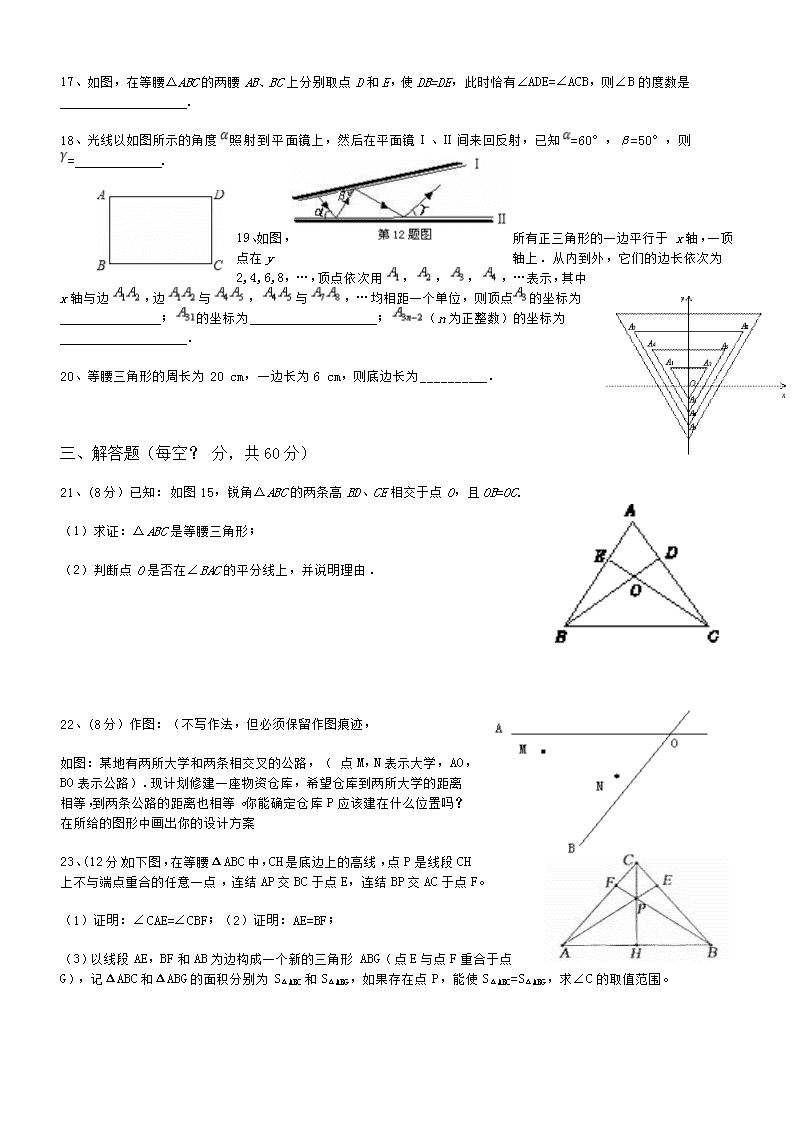
八年级上册数学等腰三角形测试题

梅川高中学校八年学年度上学期等腰三角形测试题 ‎ 命题：张俊超 ‎ 一、选择题（每空3 分，共30 分）‎ ‎1、如图4237，在△ABC中，AC＝AD＝BD，∠DAC＝80°，则∠B的度数是(　　) ‎ A．40°  B．35°  C．25°  D．20°       ‎ ‎2、图6，△ABC中，AB=AC，点D、E、F分别在BC、AB、AC上，且DE=BE，DF=DC，若∠A=40°，则∠EDF的度数为(   )‎ A.45°             B.60°            C.70°                 D.80°‎ ‎3、如图,周长为,点、都在边上，的平分线垂直于，垂足为，平分线垂直于，垂足为，若，则的长为--------（      ）‎ A．3　　　        B．　　　     C．　　            D． ‎ ‎4、已知BD是等腰的角平分线，如果，那么等于 （     ）． ‎ A．     B．       C．        D．或或 ‎5、如图，在Rt△ABC中，CD⊥AB，∠A＝30°，BD＝4cm，则AB＝（   ）‎ A、1cm              B、2cm          C、8cm    D、16cm ‎6、等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（    ）‎ A、60°  B、120°    C、60°或150°  D、60°或120°‎ ‎7、如图，正方形ABCD中，在AD的延长线上取点E，F，使DE=AD，DF=BD，连接BF分别交CD，CE于H，G下列结论：‎ ‎①EC=2DG；②；③；④图中有8个等腰三角形。其中正确的是（  ）‎ A、①③        B、②④         C、①④        D、②③‎ ‎8、把两个都有一个锐角为30°的一样大小的直角三角形拼成如图5所示的图形，两条直角边在同一直线上．则图中等腰三角形有（    ）个. ‎ A．1个                B．2个             C．3个           D．4个 ‎9、如图，等边△ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点，若AE=2，当EF+CF取最小值时，则∠ECF的度数为 ‎    A.  30°     B.  22.5°     C.  15°     D.  45°‎ ‎10、如图，△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC的方向平移，得到△A′B′C′，再将△A′B′C′绕点A′逆时针旋转一定角度后，点B′恰好与点C重合，则平移的距离和旋转角的度数分别为（　　）‎ ‎　‎ A．‎ ‎4，30°‎ B．‎ ‎2，60°‎ C．‎ ‎1，30°‎ D．‎ ‎3，60°‎ 二、填空题（每空3 分，共30 分）‎ ‎11、如图12，已知∠AOB=，在射线OA、OB上分别取点A1、B1，使OA1=OB1，连接，在，上分别取点、，使，连接，…，按此规律下去，记∠A2B1B2=θ1，∠A3B2B3=θ2，…，∠An+1BnBn+1=θn，则θ1=___________；θn=___________.‎ ‎ 12、如图，已知AB=2，P是线段AB上的动点，分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连接EF，设EF的中点为G，连接PG，则PG的最小值是_______.‎ ‎13、如图，在△ABC中，AB＝AC，BM、CM分别是∠ABC、∠ACB的平分线，DE经过点M，且DE//BC，则图中有             个等腰三角形．‎ ‎14、如图，在△ABC中，AB=AC，∠A=40°，点D在AC上，BD=BC，则∠ABD的度数是　　°．‎ ‎15、 如图，在△ABC中，AB＝AC，∠BAC＝120°，D是BC的中点，DE⊥AC. 则AB : AE＝               .‎ ‎ ‎ ‎ 13题 14题 15题 ‎16、如图，在矩形ABCD中，AB=4，BC=6，若点P在AD边上，连接BP、PC，△BPC是以PB为腰的等腰三角形，则PB的长为　．‎ ‎17、如图，在等腰△ABC的两腰AB、BC上分别取点D和E，使DB=DE，此时恰有∠ADE=∠ACB，则∠B的度数是          .‎ ‎18、光线以如图所示的角度照射到平面镜上，然后在平面镜Ⅰ、Ⅱ间来回反射，已知=60°，β=50°，则=       .‎ ‎19、如图，所有正三角形的一边平行于x轴，一顶点在y轴上．从内到外，它们的边长依次为2,4,6,8，…，顶点依次用，，，，…表示，其中x轴与边，边与，与，…均相距一个单位，则顶点的坐标为        ；的坐标为          ；（n为正整数）的坐标为          ．‎ ‎20、等腰三角形的周长为20 cm，一边长为6 cm，则底边长为__________．   ‎ ‎  ‎ 三、解答题（每空？ 分，共60分）‎ ‎21、(8分）已知：如图15，锐角△ABC的两条高BD、CE相交于点O，且OB=OC.‎ ‎（1）求证：△ABC是等腰三角形；‎ ‎（2）判断点O是否在∠BAC的平分线上，并说明理由.‎ ‎22、(8分）作图：（不写作法，但必须保留作图痕迹， ‎ 如图：某地有两所大学和两条相交叉的公路，（点M，N表示大学，AO，BO表示公路）.现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等。你能确定仓库P应该建在什么位置吗？在所给的图形中画出你的设计方案 ‎23、(12分）如下图，在等腰ΔABC中，CH是底边上的高线，点P是线段CH上不与端点重合的任意一点，连结AP交BC于点E，连结BP交AC于点F。‎ ‎（1）证明：∠CAE=∠CBF；（2）证明：AE=BF；‎ ‎（3）以线段AE，BF和AB为边构成一个新的三角形ABG（点E与点F重合于点G），记ΔABC和ΔABG的面积分别为SΔABC和SΔABG，如果存在点P，能使SΔABC=SΔABG，求∠C的取值范围。‎ ‎24、(10分）如图，△ABC中，∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始，‎ 按C→A→B→C的路径运动，且速度为每秒2cm，设运动的时间为t秒。‎ ‎（1）当t为何值时，CP把△ABC的周长分成相等的两部分。‎ ‎（2）当t为何值时，CP把△ABC的面积分成相等的两部分，并求出此时CP的长；‎ ‎（3）当t为何值时，△BCP为等腰三角形？‎ ‎25、(10分）已知，△ABC为等边三角形，点D为直线AB上一动点（点D不与A、B重合）．以CD为边作菱形CDEF，使∠DCF=60°，连接AF．‎ ‎⑴如图1，当点D在边AB上时，‎ ‎①求证：∠BDC=∠AFC；‎ ‎②请直接判断结论∠A FC=∠BAC＋∠ACD是否成立？‎ ‎⑵如图2，当点D在边BA的延长线上时，其他条件不变，结论∠A FC=∠BAC＋∠ACD是否成立？请写出∠AFC、∠BAC、∠ACD之间存在的数量关系，并写出证明过程；‎ ‎⑶如图3，当点D在边AB的延长线上时，且点C、F分别在直线AB的异侧，其他条件不变，请补全图形，并直接写出∠AFC、∠BAC、∠ACD之间存在的等量关系．‎ ‎26、(12分）如图，点O是等边△ABC内一点，∠AOB=110°，∠COB=，将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．‎ ‎（1）证明：△COD是等边三角形；‎ ‎（2）当=150°时，判断△AOD的形状，并说明理由；‎ ‎（3）探究：当为多少度时，△AOD是等腰三角形？‎ 参考答案 一、选择题 ‎1、C　 2、C   3、A 4、D 5、B 6、D 7、D8、C． 9、A 10、B 二、填空题 ‎11、；12、13、五； 14、3015、  4 : 1         16、，PB的长度是5或6．‎ ‎17、  36o ‎ ‎18、40°  解析：=180°-[60°+（180°-100°）]=40°．‎ ‎19、， ，．‎ ‎20、8 cm或6 cm； ‎ 三、简答题 ‎21、（1）证明：如答图5，∵OB=OC,∴∠OBC=∠OCB,∵BD、CE是两条高,∴∠BDC=∠CEB=‎ ‎90°,又∵BC=CB ，∴△BDC≌△CEB（AAS），‎ ‎∴∠DCB=∠EBC,∴AB=AC,∴△ABC是等腰三角形.‎ ‎（2）解：点O在∠BAC的平分线上.如答图5，连接AO.‎ ‎ ‎ 答图5‎ ‎∵ △BDC≌△CEB,∴BD=CE,又∵OB=OC,∴ OD=OE.‎ 又∵∠BDA=∠CEA=90°,AO=AO,∴Rt△ADO≌Rt△AEO（HL）,‎ ‎∴∠DAO=∠EAO，∴点O在∠BAC的平分线上.‎ 四、作图题 ‎22、略 五、计算题 ‎23、证明：(1) ∵△是等腰△，是底边上的高线，∴，‎ 又∵, ∴△ ≌△，‎ ‎∴, 即;        ‎ ‎(2) ∵, ，,‎ ‎∴△ ≌△，∴;          ‎ ‎(3) 由(2)知△是以为底边的等腰△，∴ 等价于，‎ ‎1）当∠为直角或钝角时，在△中，不论点在何处，均有，所以结论不成立;‎ ‎2）当∠为锐角时， ∠，而，要使，只需使∠ =∠，此时，∠180°2∠，‎ 只须180°2∠∠，解得 60°∠ 90°.  ‎ 六、综合题 ‎24、 ‎ ‎25、(1)①-------2’②-------成立-------3‘‎ ‎（2）不成立------4‘‎ ‎∠AFC=∠BAC-∠ACD证明-----7‘‎ ‎（3）图-----8‘‎ ‎∠AFC+∠ACD=2∠BAC-----9’‎ ‎26、解：（1）∵△ADC是由△BOC绕点C按顺时针方向旋转60°而得 ‎∴ CO=DO，∠OCD=60°     ∴∠COD=∠ODC=（180°－60°）=60°‎ ‎∴CO=DO=CD  ∴△COD为等边三角形                  …………………4分 ‎（2）当a=150°时，∠ADC=∠BOC=150°‎ ‎     ∵△COD为等边三角形   ∴∠ODC=60°  ∴∠ADO=∠ADC－∠ODC=150°－60°=90 °‎ 又∵∠AOD=360°－110°－150°－60°=40°  ∴△AOD为直角三角形………………8分