- 2021-10-27 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版数学八年级下册同步练习课件-第18章-平行四边形复习与巩固18
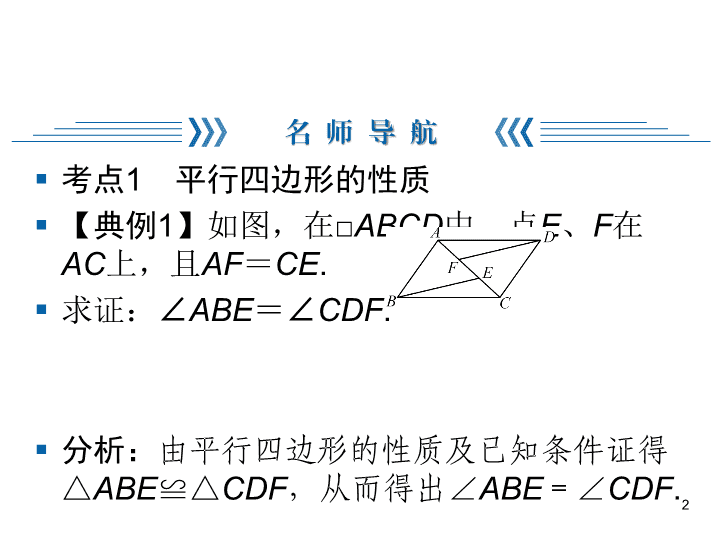
第18章 平行四边形 《平行四边形》复习与巩固 § 考点1 平行四边形的性质 § 【典例1】如图,在□ABCD中,点E、F在 AC上,且AF=CE. § 求证:∠ABE=∠CDF. § 分析:由平行四边形的性质及已知条件证得 △ABE≌△CDF,从而得出∠ABE=∠CDF.2 § 点评:证明两条线段相等或两个角相等,一般是通过证明线段或角所在 的三角形全等来解决,而根据平行四边形的性质可以得出三角形全等的 条件. 3 § 【典例2】已知□ABCD的周长为30 cm,它 的对角线AC和BD交于点O,且△AOB的周 长比△BOC的周长长5 cm,求AB、AD的 长. 4 § 解答:∵△AOB的周长比△BOC的周长长5 cm, § ∴AO+AB+BO-(BO+OC+BC)=5 cm. § ∵四边形ABCD是平行四边形, § ∴AD=BC,AO=OC, § ∴AB-BC=5 cm. § ∵□ABCD的周长为30 cm, § ∴AB+BC=15 cm, § ∴AB=10 cm,BC=5 cm, § ∴AD=BC=5 cm. § 点评:平行四边形的两条对角线互相平分,把平行四边形分成两 对全等的三角形,相邻的两个三角形的周长差等于平行四边形邻 边的长度差. 5 § 考点2 平行四边形的判定 § 【典例3】如图,E、F为□ABCD的对角线 AC所在直线上的两点,且AE=CF.求证:四 边形EBFD是平行四边形. § 分析:(方法一)由四边形ABCD是平行四边形, 可知AB∥CD,AB=CD,则∠BAC= ∠DCA,故∠BAE=∠DCF.又AE=CF,从 而可得△BAE≌△DCF,则BE=DF.同理可 得DE=BF,即可证得结论;(方法二)从对角 线入手,这两个四边形具有共同的对角线BD, 因此连结BD,证出EF、BD互相平分,亦可 证得结论. 6 § 证明:(方法一)∵四边形ABCD为平行四边形, § ∴AB∥CD,AB=CD,∴∠BAC=∠DCA,∴∠BAE=∠DCF. § 又∵AE=CF,∴△BAE≌△DCF,∴BE=DF. § 同理可得DE=BF. § ∴四边形EBFD是平行四边形. § (方法二)连结BD交AC于点O. § ∵四边形ABCD为平行四边形,∴AO=CO,BO=DO. § 又∵AE=CF,∴AO+AE=CO+CF,即OE=OF, § ∴四边形EBFD是平行四边形. § 点评:(1)各种判定方法互相关联,认真观察题中的条件,选择恰 当的判定方法.(2)平行四边形的判定经常与性质联系在一起,要 注意它们的区别和联系. 7 § ★考点1 平行四边形的性质 § 1.如图,□ABCD的对角线AC、BD相交于点O,EF过点O与AD、 BC分别相交于点E、F,若AB=4,BC=5,OE=1.5,那么四边 形EFCD的周长为( ) § A.16 B.14 § C.12 D.10 8 C § 2.如图,在□ABCD中,已知AD=12 cm,AB=6 cm,AE平分 ∠BAD交BC于点E,则CE的长等于( ) § A.8 cm B.6 cm § C.4 cm D.2 cm § 3.如图,□ABCD的对角线AC、BD相交于点O,则下列说法一 定正确的是 § ( ) § A.AO=OD B.AO⊥OD § C.AO=OC D.AO⊥AB 9 B C 10 6 6 § 6.【江苏无锡中考】如图,平行四边形 ABCD中,E、F分别是边BC、AD的中点, 求证:∠ABF=∠CDE. 11 § ★考点2 平行四边形的判定 § 1.在下列给出的条件中,不能判定四边形ABCD是平行四边形的 是( ) § A.AB=CD,AD=BC B.AB∥CD,AD=BC § C.AB∥CD,AB=CD D.AB∥CD,AD∥BC § 2.如图,在△ABC中,AB=6,AC=10,点D、E、F分别是AB、 BC、AC的中点,则四边形ADEF的周长为( ) § A.8 B.10 § C.12 D.16 12 B D § 3.【安徽中考】□ABCD中,E、F是对角 线BD上不同的两点.下列条件中,不能得出 四边形AECF一定为平行四边形的是( ) § A.BE=DF B.AE=CF § C.AF∥CE D.∠BAE=∠DCF § 解析:如图,连结AC与BD相交于点O.在 □ABCD中,OA=OC,OB=OD,要使四 边形AECF为平行四边形,只需证得OE=OF 即可.若BE=DF,则OB-BE=OD-DF, 即OE=OF,故A不符合题意;若AE=CF, 则无法判断OE=OF,故B符合题意;由 AF∥CE能够利用“角边角”证得 △AOF≌△COE,从而得到OE=OF,故C 不符合题意;由∠BAE=∠DCF能够利用 “角边角”证得△ABE≌△CDF,从而得到 BE=DF,然后同A,故D不符合题意.故选 B. 13 B § 4.如图,四边形ABCD的对角线交于点O,从下列条件: ①AD∥BC;②AB=CD;③AO=CO;④∠ABC=∠ADC中, 选出两个可使四边形ABCD是平行四边形,则你选的两个条件是 ____________________.(填写一组序号即可) 14 ①③(答案不唯一) § 5.如图,在四边形ABCD中,AD∥BC,延长 BC到点E,使CE=BC,连结AE交CD于点F,点 F是CD的中点.求证: § (1)△ADF≌ △ECF; § (2)四边形ABCD是平行四边形. 15 § 6.如图,四边形ABCD中,BD垂直平分AC, 垂足为F,E为四边形ABCD外一点,且 ∠ADE=∠BAD,AE⊥AC. § (1)求证:四边形ABDE是平行四边形; § (2)如果DA平分∠BDE,AB=5,AD=6,求 AC的长. 16查看更多