- 2021-10-27 发布 |
- 37.5 KB |
- 3页


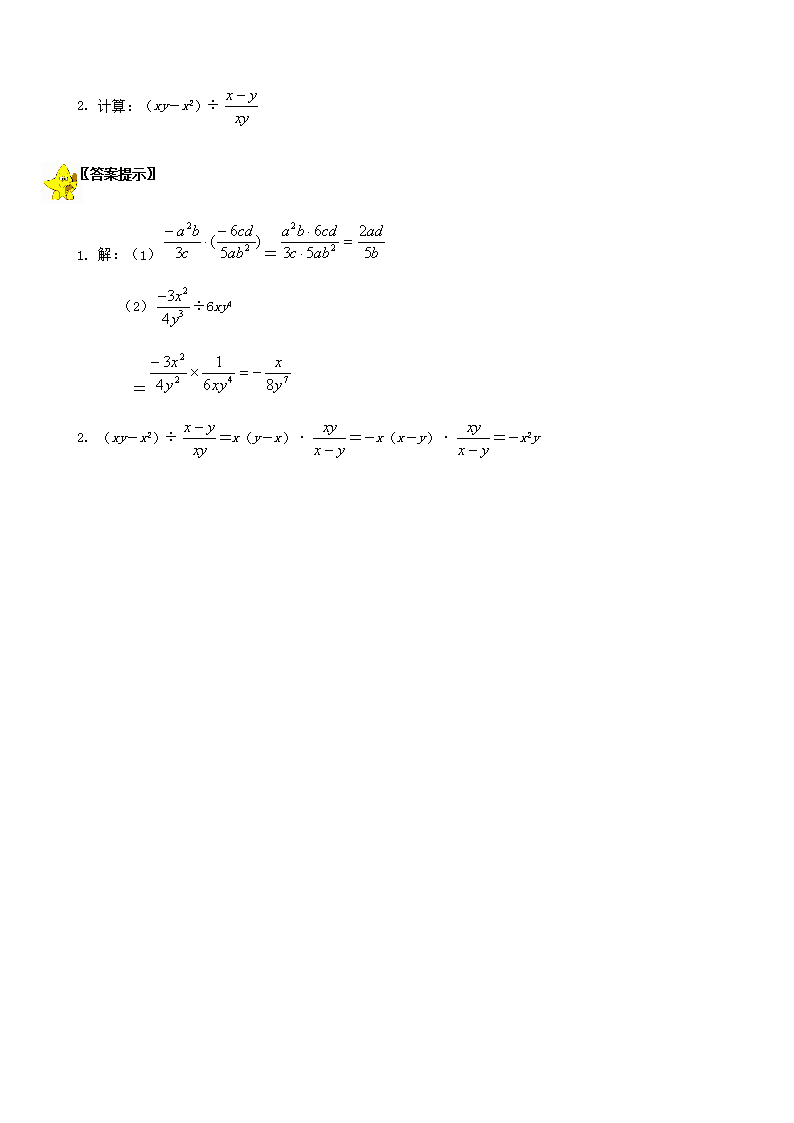
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上分式的乘除 冀教
14.2 分式的乘除 〖教学目标〗 (-)知识目标(调整:把教材的乘除法安排为一课时,第二课时安排乘除法的巩固与提高) 1.分式乘除法的运算法则, 2.会进行分式的乘除法的运算. (二)能力目标 1.类比分数乘除法的运算法则.探索分式乘除法的运算法则. 2.在分式乘除法运算过程中,体会因式分解在分式乘除法中的作用,发展有条理的思考和语言表达能力. (三)情感目标 通过师生共同交流、探讨,使学生在掌握知识的基础上,认识事物之间的内在联系,获得成就感. 〖教学重点〗 让学生掌握分式乘除法的法则及其应用. 〖教学难点〗 分子、分母是多项式的分式的乘除法的运算. 〖教学过程〗 一、课前布置 自学:阅读课本P32~P34,试着做一做本节练习,提出在自学中发现的问题(鼓励提问). 二、学情诊断 1.了解学生原有认知机构,解答学生提出的问题. 三、师生互动 [师]上节课,我们是运用与分数类比的方法,研究了分式的基本性质,那么分式的运算是否也可以和分数的运算类似呢? 通过自学,你能做分式的乘法运算吗,谁来说一说你是怎样做的? [生]两个分数相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母; 所以我很快记住了分式相乘的法则:两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母. [师]很好,你能通过这两道题来说一说怎样运用法则进行分式乘法计算吗? (提供例题,让学生讲解) 1. (1)·;(2)·. 解:(1)·===; (2)· ==. 强调:运算结果如不是最简的分式时,一定要进行约分,使运算结果化为最简 ,即分子分母没有公因式. [师]你认为进行分式乘法运算的关键步骤是什么? [生]关键步骤是约分. 如果分子分母是多项式,我们还要能正确地将分子、分母因式分解,然后再约分化简. (二) [师生共析]同样我们也可以运用分数的除法法则得到分式的除法, 两个分数相除,把除数的分子和分母颠倒位置后,再与被除数相乘. 两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘. [师]强调分式的除法实际上是转化为分式的乘法后再进行运算,怎样转化——把除式的分子和分母颠倒位置后再与被除式相乘.因此进行分式除法运算的关键步骤是体现转化的这一步. (鼓励学生讲解教师提供的例题.) 2. 计算: (1)3xy2÷ ;(2)÷. 分析:(1)将算式对照分式的除法运算法则,进行运算;(2)当分子、分母是多项式时,一般应先分解因式,并在运算过程中约分,可以使运算简化,避免走弯路. 解:(1)3xy2÷=3xy2· ==x2; (2)÷ =× = =. 四、补充练习 作业P33习题1,P35习题1 〖分层练习〗 1. 计算:(1) (2)÷6xy4 2. 计算:(xy-x2)÷ 〖答案提示〗 1. 解:(1)= (2)÷6xy4 = 2. (xy-x2)÷=x(y-x)·=-x(x-y)·=-x2y查看更多