_ 沪科版数学七年级上册期末测试卷（含答案安徽专用）

_ 沪科版数学七年级上册期末测试卷（含答案安徽专用）

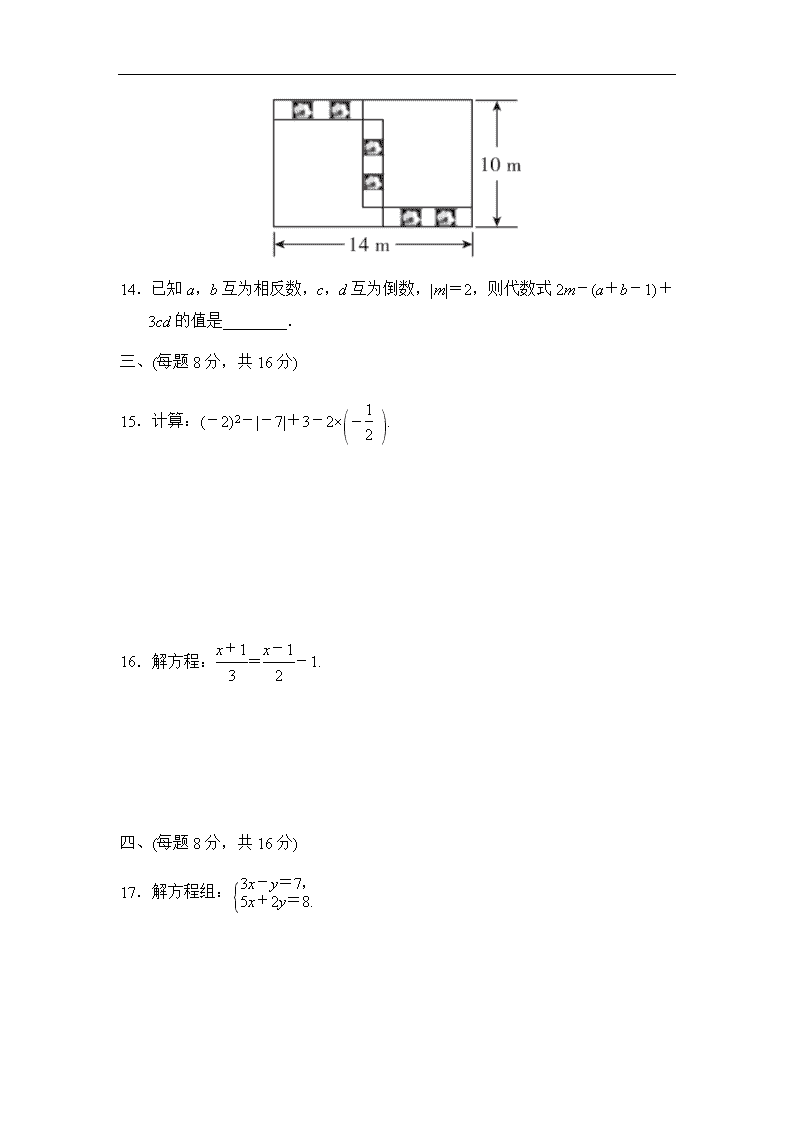
2020-2021 沪科版七年级数学上期期末测试卷（安徽专用） 一、选择题(每题 4 分，共 40 分) 1．－3 2 的相反数是( ) A．3 2 B．－3 2 C．2 3 D．－2 3 2．下列变形符合等式基本性质的是( ) A．如果 2x－y＝7，那么 y＝7－2x B．如果 ak＝bk，那么 a＝b C．如果－2x＝5，那么 x＝5＋2 D．如果－1 3a＝1，那么 a＝－3 3．多项式 x2y3－3xy3－2 的次数和项数分别为( ) A．5，3 B．5，2 C．2，3 D．3，3 4．已知∠α与∠β互补，∠α＝150°，则∠β的余角的度数是( ) A．30° B．60° C．45° D．70° 5．中华汉字，源远流长．某校为了传承中华优秀传统文化，组织了一次全校 3 000 名学生参加的“汉字听写”大赛．为了解本次大赛的成绩，学校随机抽取了其 中 200 名学生的成绩进行统计分析，下列说法正确的是( ) A．3 000 名学生的“汉字听写”大赛成绩是总体 B．每名学生是个体 C．200 名学生是总体的一个样本 D．样本容量是 3 000 6．下列说法中，正确的是( ) A．－a 的相反数是正数 B．两点之间的线段叫两点之间的距离 C．两条射线组成的图形叫做角 D．两点确定一条直线 7．一个整式减去 a2－b2 后所得的结果是－a2－b2，则这个整式是( ) A．－2a2 B．－2b2 C．2a2 D．2b2 8．已知 x＝0， y＝2 和 x＝4， y＝1 都是方程 mx＋ny＝8 的解，则 m，n 的值分别为( ) A．1，－4 B．－1，4 C．－1，－4 D．1，4 9．将一副三角尺如图放置，∠COD＝20°，则∠AOB 的度数为( ) A．140° B．150° C．160° D．170° 10．两根木条，一根长 20 cm，另一根长 24 cm，将它们一端重合且放在同一条 直线上，此时两根木条的中点之间的距离为( ) A．2 cm B．4 cm C．2 cm 或 22 cm D．4 cm 或 44 cm 二、填空题(每题 5 分，共 20 分) 11．某班班主任把本班学生体育期末考试成绩绘制成扇形统计图，已知全班有 40 名学生，其中体育成绩优秀的学生有 18 名，则代表体育成绩优秀的扇形 所对应的圆心角度数是________． 12．代数式 x2＋x－2 的值为 0，则代数式 2x2＋2x－3 的值为________． 13．如图，在长为 14 m，宽为 10 m 的长方形展厅中划出三个形状、大小完全一 样的小长方形摆放水仙花，则每个小长方形的周长为________m. 14．已知 a，b 互为相反数，c，d 互为倒数，|m|＝2，则代数式 2m－(a＋b－1) ＋3cd 的值是________． 三、(每题 8 分，共 16 分) 15．计算：(－2)2－|－7|＋3－2× －1 2 . 16．解方程：x＋1 3 ＝x－1 2 －1. 四、(每题 8 分，共 16 分) 17．解方程组： 3x－y＝7， 5x＋2y＝8. 18.我们规定“ △ ”是一种数学运算符号，两数 a，b 通过“ △ ”的运算是 a－b＋ab， 即 a △ b＝a－b＋ab，例如：3 △ 5＝3－5＋3×5＝13. (1)求 2 △ (－3)的值； (2)求(－5) △ [1 △ (－2)]的值． 五、(每题 10 分，共 20 分) 19．一种蔬菜 x 千克，不加工直接出售每千克可卖 y 元；如果经过加工质量减少 了 20%，价格增加了 40%. (1)1 000 千克这种蔬菜，加工后出售一共卖 2 576 元，问 1 000 千克这种蔬菜不 加工直接出售每千克可卖多少钱？ (2)1 000 千克这种蔬菜加工后出售比不加工直接出售一共多卖多少钱？ 20．甲、乙两人分别从 A，B 两地同时出发，甲骑自行车，乙骑摩托车，沿同一 条直线形公路相向匀速行驶，出发后经 3 小时两人相遇．已知在相遇时乙比 甲多行驶了 90 千米，相遇后经 1 小时乙到达 A 地． (1)甲、乙行驶的速度分别是多少？ (2)甲、乙行驶多少小时时，两人相距 30 千米？ 六、(12 分) 21．如图，点 O 是直线 AB 上一点，OC 平分∠AOB，在直线 AB 另一侧，以 O 为顶点，作∠DOE＝90°. (1)若∠AOE＝48°，求∠BOD 的度数； (2)写出图中与∠AOE 互余的角； (3)∠AOE 与∠COD 有什么数量关系？请写出你的结论并说明理由． 七、(12 分) 22．今年 4 月，国民体质监测中心等机构开展了青少年形体测评．专家组随机抽 查了某市若干名初中学生坐姿、站姿、走姿的好坏情况．我们对专家的测评 数据进行了适当处理(如果一名学生有一种以上不良姿势，我们以他最突出的 一种记录)，将统计结果绘制成如图所示的两幅不完整的统计图．请你根据图 中所给信息解答下列问题． (1)在这次形体测评中，一共抽查了多少名学生？ (2)请你将两幅统计图补充完整； (3)根据统计结果，请你简单谈谈自己的看法． 八、(14 分) 23．某蔬菜公司收购蔬菜进行销售的获利情况如下表所示： 销售方式 直接销售 粗加工后销售 精加工后销售 每吨获利/元 100 250 450 现在该公司收购了 140 吨蔬菜，已知该公司每天能精加工蔬菜 6 吨或粗加工 蔬菜 16 吨．(两种加工方式不能同时进行) (1)如果要求在 18 天内把这 140 吨蔬菜全部销售完，请完成下面的表格： 销售方式 全部直接销售 全部粗加工后销售 尽量精加工，剩余部分直接销售 获利/元 (2)若先进行精加工，然后进行粗加工，要求在 15 天内刚好加工完这 140 吨蔬菜， 则应如何分配加工时间？ 答案 一、1.A 2.D 3.A 4.B 5.A 6.D 7．B 8.D 9.C 10.C 二、11.162° 12.1 13.16 14．8 或 0 点拨：根据题意，得 a＋b＝0，cd＝1，m＝2 或 m＝－2， 当 m＝2 时，原式＝2×2－(0－1)＋3×1＝4＋1＋3＝8； 当 m＝－2 时，原式＝2×(－2)－(0－1)＋3×1＝－4＋1＋3＝0. 综上所述，代数式 2m－(a＋b－1)＋3cd 的值是 8 或 0. 三、15.解：(－2)2－|－7|＋3－2× －1 2 ＝4－7＋3＋1＝1. 16．解：去分母，得 2(x＋1)＝3(x－1)－6， 去括号，得 2x＋2＝3x－3－6， 移项，得 2x－3x＝－3－6－2， 合并同类项，得－x＝－11， 系数化为 1，得 x＝11. 四、17.解： 3x－y＝7，① 5x＋2y＝8.② ①×2＋②，得 11x＝22，解得 x＝2. 把 x＝2 代入①，得 6－y＝7.解得 y＝－1. 所以原方程组的解为 x＝2， y＝－1. 18．解：(1)因为 a △ b＝a－b＋ab， 所以 2 △ (－3)＝2－(－3)＋2×(－3)＝2＋3＋(－6)＝－1. (2)(－5) △ [1 △ (－2)] ＝(－5) △ [1－(－2)＋1×(－2)] ＝(－5) △ (1＋2－2) ＝(－5) △ 1 ＝(－5)－1＋(－5)×1 ＝(－5)－1＋(－5) ＝－11. 五、19.解：(1)由题意知 x 千克这种蔬菜加工后的质量为(1－20%)x 千克，价格为 每千克(1＋40%)y 元． 因为 1 000 千克这种蔬菜，加工后出售一共卖 2 576 元，1 000×(1－20%)＝ 800(千克)， 所以 800(1＋40%)y＝2 576， 解得 y＝2.3. 答：1 000 千克这种蔬菜不加工直接出售每千克可卖 2.3 元． (2)2 576－2.3×1 000＝276(元)． 答：1 000 千克这种蔬菜加工后出售比不加工直接出售一共多卖 276 元． 20．解：(1)设甲、乙行驶的速度分别是 x 千米/时、y 千米/时，根据题意，得 3x＋90＝3y， y＝3x， 解得 x＝15， y＝45， 所以甲、乙行驶的速度分别是 15 千米/时、45 千米/时． (2)由(1)可得 A，B 两地相距 45×(3＋1)＝180(千米)，设甲、乙行驶 z 小时时，两 人相距 30 千米，根据题意，得两人行驶的总路程是(180－30)千米或(180＋ 30)千米，则(45＋15)z＝180－30 或(45＋15)z＝180＋30，解得 z＝5 2 或 z＝7 2 ， 所以甲、乙行驶5 2 小时或7 2 小时时，两人相距 30 千米． 六、21.解：(1)因为∠AOE＝48°，∠DOE＝90°， 所以∠BOD＝180°－90°－48°＝42°. (2)因为∠DOE＝90°， 所以∠AOE＋∠BOD＝180°－90°＝90°， 所以图中与∠AOE 互余的角是∠BOD. (3)∠AOE＋∠COD＝180°. 理由如下： 因为 OC 平分∠AOB， 所以∠AOC＝∠BOC＝90°. 因为∠AOE＋∠BOD＝90°， 所以∠AOE＋∠COD＝∠AOE＋∠BOD＋∠BOC＝90°＋90°＝180°. 七、22.解：(1)100÷20%＝500(名)． 答：一共抽查了 500 名学生． (2)“三姿良好”所占百分率为 1－20%－37%－31%＝12%，“三姿良好”的学生有 500×12%＝60(名)．如图．补全两幅统计图． (3)三姿良好的人数比例极低，说明青少年学生重视自己的坐姿、站姿、走姿的 人数少，这对学生的健康成长不利，要加强教育和引导．(答案不唯一) 八、23.解：(1)14 000；35 000；51 800 (2)设应安排 x 天进行精加工，y 天进行粗加工， 由题意，得 x＋y＝15， 6x＋16y＝140. 解得 x＝10， y＝5. 故应安排 10 天进行精加工，5 天进行粗加工．