- 2021-10-27 发布 |
- 37.5 KB |
- 23页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下数学课件《二次根式》 (17)_苏科版
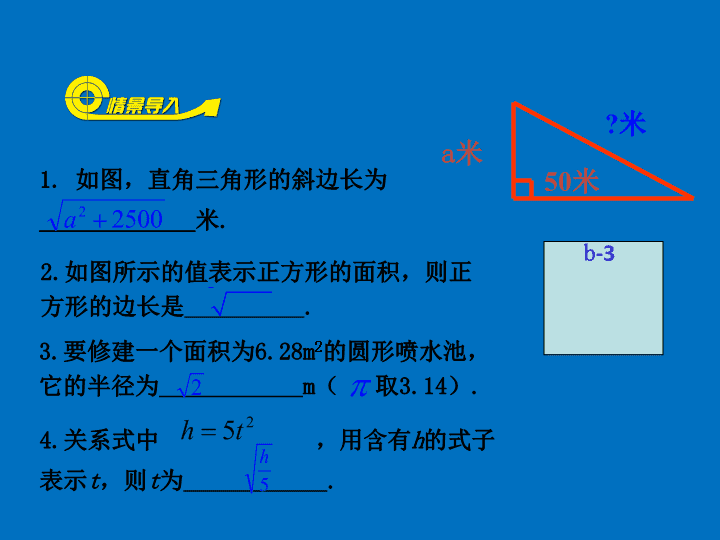
2.7 二次根式 2.如图所示的值表示正方形的面积,则正 方形的边长是 .3b b-3 3.要修建一个面积为6.28m2的圆形喷水池, 它的半径为 m( 取3.14).2 4.关系式中 ,用含有h的式子 表示t,则t为 . 25th 5 h 1. 如图,直角三角形的斜边长为 _____________米. 50米 a米 ?米 25002 a 1.知识目标 (1)掌握二次根式的概念和性质,会确定被开方数的取值 范围; (2)能利用积(或商)的算术平方根的性质进行二次根式 的化简和运算. 2.教学重点 二次根式的加减乘除运算. 3.教学难点 二次根式的乘除法与二次根式的积(或商)的算术平方根 的关系及应用. 观察以上各式,它们有什么共同特点? 表示一些正数的算术平方根 3b 2 5 h 25002 a (一)二次根式 2. a可以是数,也可以是式 3. 形式上含有二次根号 4. a≥0, ≥0 a 5.既可表示开方运算,也可表示运算的结果 1.表示a的算术平方根 ( 双重非负性) a形如 (a≥0)的式子叫做二次根式 (二)计算下列各式, 观察计算结果,你发现什么规律 41. × =____9 _____94 _____2516___,2516.2 用你发现的规律填空,并用计算器验算 10___52.2 ;6___32.1 思考: 6 6 20 20 = = 计算的结果有什么规律?你能用含字母 的式子表示吗? 二次根式的乘法法则 积的算术平方根的性质 a、b必须都是非负数! (a≥0,b≥0) (a≥0,b≥0)baab . 4 3 4 3 3 2 3 2 = = 0.8165 0.6325 = = 计算的结果有什么规律?你能用含字母的 式子表示吗? 二次根式的除法法则 商的算术平方根的性质 a b = a b (a≥0,b>0) a b = a b (a≥0,b>0) (四) 1.满足哪些条件的二次根式,叫做最简二次根式? (1)被开方数不含分母;也就是被开方数是整数或整式; (2)被开方数中不含能开得尽方的因数或因式. 2.化简二次根式的一般步骤: 化去根号下的分母,并把被开方数中能开得尽方 的因数或因式用它的算术平方根代替后移到根号 外面,化简时,依照二次根式的有关性质进行. 例1 求下列二次根式中字母的取值范围: 11 a a21 12 求二次根式中字母的取值范围的基本依据: ①被开方数不小于零; ②分母中有字母时,要保证分母不为零. 解(1) a≥-1; (2) a< (3) a为任何实数. 2 1 233 a ;4281161 2. 32 ba);()( 化简:例 8116(1):解 8116 3694 3242 ba)( 324 ba bba 22 bba 22 bab2 解: (1) 3 24 22248 3 24 ; (2) 18 1 2 3 339318 2 3 18 1 2 3 例3 计算 . 18 1 3 2)2(; 3 24)1( x x 1)4(4)3( 2 1. x取何值时,下列二次根式有意义? xx 3)2(1)1( 为全体实数x 0x 3)5( x 2 1)6( x 0x 跟踪练习 x≥0 x≤0 x≥0 ( ) ( ), 时,当 yx yx 031.2 . 02365.3 2 的值求 已知 xyz zyx 112 xx xx 631 23 2 x 14 x 2 2a b , 2 0a , 02 b 2 2( 2)a b 原式 2 2( 2 2) 2 4 拔尖自助餐 设a、b为实数,且| 2 -a|+ b-2 =0√ 2 2a b , (1) 求a2 -2 a+2+b2的值.2 a ≥ ≥b a b 1.下列运算正确的是 [ ] A 当堂检测 2.填空 - 4 13 A. 52×32 = 52 × 32= 5×3=15 B. 52 - 32 = 52 - 32= 5 - 3=15 153 3 5 C. D. 8)4()2(164)16()4( 9 4112 8.64 -3- 10 A 选做题(A组) 的值是3223.1 . 56.D36.C12.B66.A 3240.649004.0.2 . . )103()103(3. 1995 1996 选做题 (B组) B 36.D8.C63.B9.A 3)32.(1 的值是. A xxxx xx 6.D6.C6.B6.A )32.2 的值是. 2 D. 310.D3.C3.B310.A )310()310.(3 的值是 2 二 次 根 式 三个概念 两个公式 三个性质 四种运算 二次根式 最简二次根式 b a b a )0,0( ba 0,0 babaab1、 2、 加 、减、乘、除 知识结构 2( )a a 2 , 0 , 0{ a a a aa a 0 0a ( a )查看更多