八年级下册数学同步练习2-5-1 矩形的性质 湘教版

八年级下册数学同步练习2-5-1 矩形的性质 湘教版

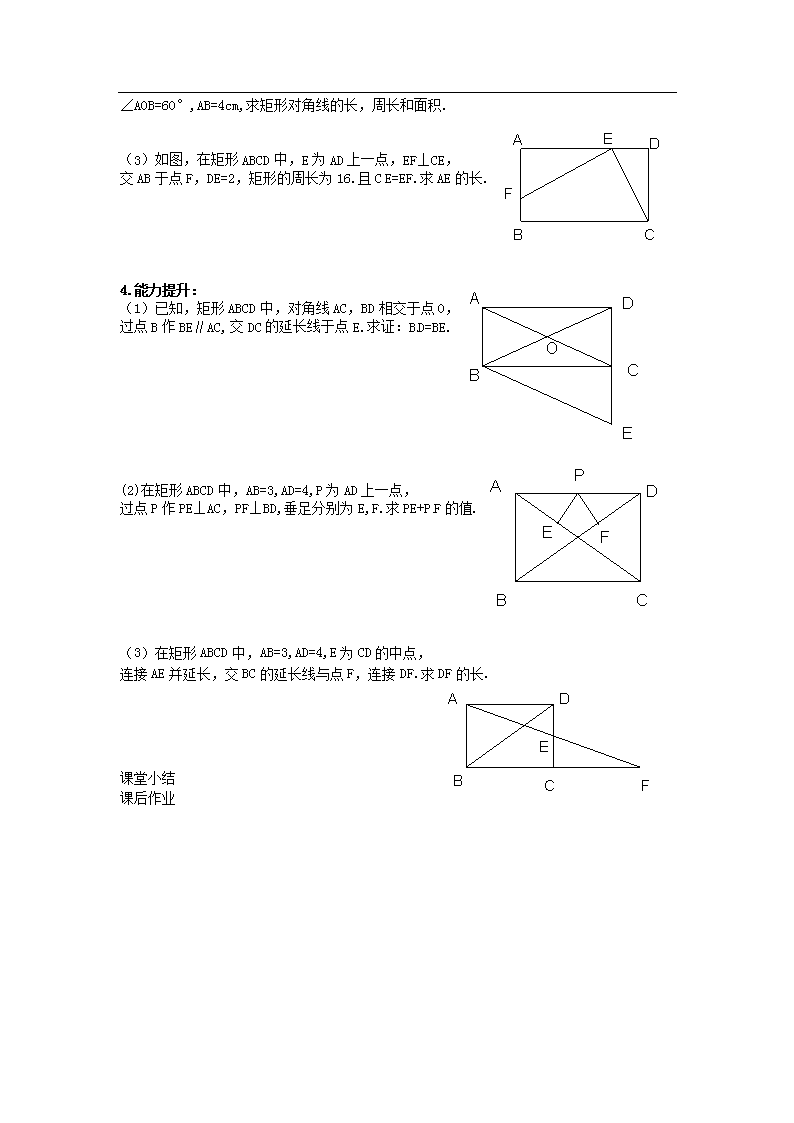
‎2.5 矩 形 ‎2.5.1 矩形的性质 学习目标：1、理解矩形的意义，知道矩形与平行四边形的区别与联系.‎ ‎2、掌握矩形的性质定理，会用性质定理进行有关的计算与证明. ‎ 学习重点：矩形的性质.‎ 学习难点：用性质定理进行有关的计算与证明.‎ 教学方法：练讲练 学习过程： ‎ ‎1.知识回顾：如下图：‎ ‎（1）左图是一个平行四边形，回忆平行四边形有哪些性质？‎ ‎（2）四边形具有不稳定性，即当一个四边形的四条边长保持不变时，它的形状是可以变化的.现在使左图的平行四边形保持边长不变，而将一个内角的度数不断变化，那么在变化过程中，何时平行四边形的面积最大？这时这个平行四边形的内角是多少度？为什么 ‎（3）总结：矩形的定义：有一个角是 的平行四边形，叫做矩形.‎ ‎（4）练习：四边形、平行四边形、矩形有什么关系？‎ ‎2.一起探究：在上述变化过程中，当一个内角是90°时，其余三个内角各是多少度？‎ 它的两条对角线长又具有什么关系？‎ ‎（1）由于矩形是特殊的平行四边形，因此它具有平行四边形的所有性质，还具有平行四边形不具有的特殊性质.如图，同学们研究矩形的性质，填写下表：‎ 矩形的性质 边 角 对角线 对称性 具有平行四边形的所有性质 具有平行四边形不具有的特殊性质 ‎[来源:学科网]‎ ‎（2）你能证明以下性质的正确性吗？‎ ‎⑴矩形的四个角都是直角 ‎ ‎⑵矩形的对角线相等 ‎3.巩固练习 ‎（1）矩形具有而一般平行四边形不具有的性质是（ ）‎ A.对角相等 B.对边相等 C.对角线相等 D.对角线互相平分 [来源:Z,xx,k.Com]‎ ‎（2）已知矩形ABCD的两条对角线相交于点O，AB=3,BC=4,‎ 则矩形ABCD的对角行长是 ，周长是 ，‎ 面积是 .‎ 变式：右图中，如果矩形ABCD的两条对角线相交于点O,‎ ‎∠AOB=60°,AB=4cm,求矩形对角线的长，周长和面积.‎ A B C D E F ‎（3）如图，在矩形ABCD中，E为AD上一点，EF⊥CE，[来源:Z_xx_k.Com]‎ 交AB于点F，DE=2，矩形的周长为16.且CE=EF.求AE的长.‎ ‎[来源:学科网]‎ A B C D E O ‎4.能力提升：‎ ‎（1）已知，矩形ABCD中，对角线AC，BD相交于点O，‎ 过点B作BE∥AC,交DC的延长线于点E.求证：BD=BE.‎ P A B C D E F ‎(2)在矩形ABCD中，AB=3,AD=4,P为AD上一点，‎ 过点P作PE⊥AC，PF⊥BD,垂足分别为E,F.求PE+PF的值.‎ ‎（3）在矩形ABCD中，AB=3,AD=4,E为CD的中点，‎ 连接AE并延长，交BC的延长线与点F，连接DF.求DF的长.‎ A B C D F E ‎[来源:学科网ZXXK]‎ 课堂小结 课后作业