华师版数学八年级上册同步课件-第12章-12整式的乘法

华师版数学八年级上册同步课件-第12章-12整式的乘法

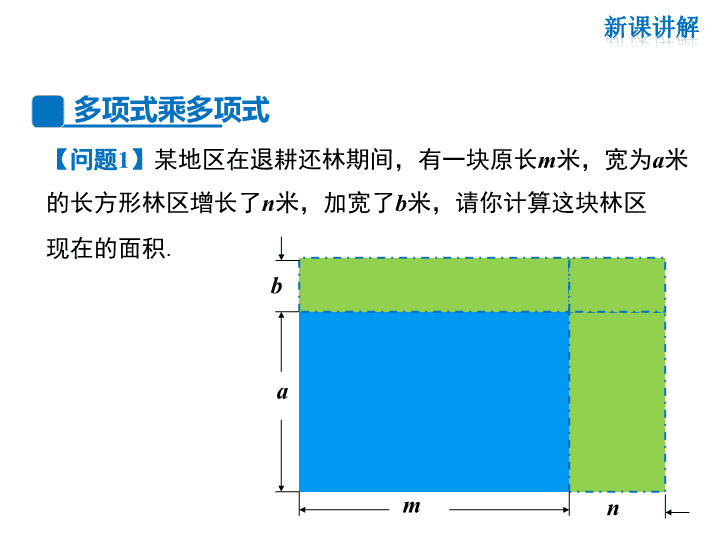
第12章 整式的乘除 12.2 整式的乘法 第3课时 多项式与多项式相乘 1.如何进行单项式与多项式乘法的运算？ （2）再把所得的积相加. （1）将单项式分别乘以多项式的各项； 2.进行单项式与多项式乘法运算时，要注意什么? （1）不能漏乘，即单项式要乘遍多项式的每一项； （2）去括号时注意符号的确定. 多项式乘多项式 【问题1】某地区在退耕还林期间，有一块原长m米，宽为a米 的长方形林区增长了n米，加宽了b米，请你计算这块林区 现在的面积. a m b n ma na mb nb a m b n 你能用不同的形式表示所拼图的面积吗？ 这块林区现在长为（m+n）米，宽为（a+b）米. (m+n)(a+b) m(a+b)+n(a+b) ma+mb+na+nb 方法一： 方法二： 方法三： 由于(m+n)(a+b)和(ma+mb+na+nb)表示同一林区的面 积，故有： (m+n)(a+b)= ma + mb + na + nb 如何进行多项式与多项式相乘的运算？ 实际上，把(a+b)看成一个整体，有： = ma+mb+na+nb (m+n)(a+b) = m(a+b)+n(a+b) (m+n)X= mX+nX？ 若X=a+b，如何计算？ 多项式与多项式相乘，先用一个多项式的每一项分别乘 以另一个多项式的每一项，再把所得的积相加. 1 2 3 4 (a+b)(m+n)=am 1 2 3 4 +an+bm+bn 多乘多，来计算，多项式各项都见面. 乘后结果要相加，化简、排列才算完. 例 计算：(1)(3x+1)(x+2)； (2)(x-8y)(x-y)； (3) (x+y)(x2-xy+y2). 解：(1) 原式=3x·x+2·3x+1·x+1×2 =3x2+6x+x+2 (2) 原式=x·x-xy-8xy+8y2 结果中有同类项 的要合并同类项. =3x2+7x+2. 计算时要注意 符号问题. =x2-9xy+8y2. (3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2 =x3-x2y+xy2+x2y-xy2+y3 = x3+y3. 计算时不能漏乘. 21 ( 2 3)( 2 ) ( 1) ;x x x   （ ） 1.判别下列解法是否正确，若错误，请说明理由. 解：原式 22 4 6 ( 1 ) ( 1 )x x x x      2 22 4 6 ( 2 1 )x x x x      2 22 4 6 2 1x x x x      2 2 5.x x   3x 22 ( 2 3)( 2 ) ( 1) ;x x x   （ ） 解：原式 )1(6342 222  xxxx 1672 22  xxx 2 7 7 .x x   ( 1)( 1)x x  2( 2 1)x x   2.计算：(1)(x−3y)(x+7y)； (2)(2x + 5y)(3x−2y). 解： (1) (x−3y)(x+7y) + 7xy −3yx− = x2 +4xy-21y2. 21y2 （2） (2x +5y)(3x−2y) = =x2 2x·3x −2x·2y +5y· 3x − 5y·2y = 6x2 −4xy+ 15xy −10y2 = 6x2 +11xy−10y2. 3.化简求值：(4x+3y)(4x-3y)+(2x+y)(3x-5y)，其中x=1，y=-2. 解：(4x+3y)(4x-3y)+(2x+y)(3x-5y) 2 2 2 2=16 12 12 9 6 10 3 5x xy xy y x xy xy y       2 222 7 14 .x xy y   当x=1，y=-2时， 原式=22×1-7×1×（-2）-14×(-2)2 =22+14 -56 =-20. 2( 2)( 3) __ __;x x x x     2( 4)( 1) __ __;x x x x     2( 4)( 2) __ __;x x x x     2( 2)( 3) __ __ .x x x x     2( )( ) _____ _____ .x a x b x x     观察上面四个等式，你能发现什么规律？并应 用这个规律解决下面的问题. ( )a b ab 5 6 (-3) (-4) 2 (-8) (-5) 6 2( 7 )( 5) __ __ .x x x x  － ＋ 2（- ） 35（- ） 4.计算： 多项式 与多项 式相乘 法 则 转化为单项式乘多项式 注 意 （1）不要漏乘； （2）正确确定各项符号； （3）结果要最简； （4）(x-1)2在一般情况下不等于x2-12 实 质 多项式与多项式相乘，先用一个多项式 的每一项分别乘以另一个多项式的每一 项，再把所得的积相加.字母表示如下： （a+b)(m+n)=am+an+bm+bn