数学人教版八年级上册教案13-1轴对称（第1课时）

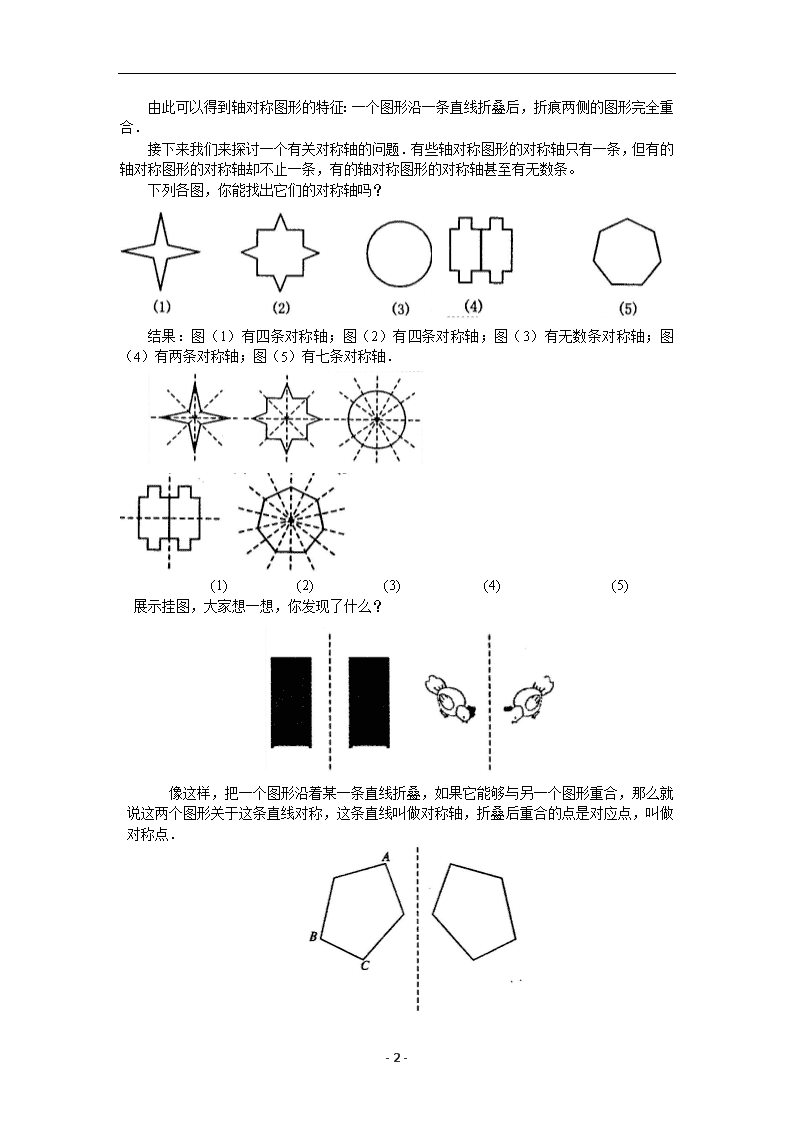
数学人教版八年级上册教案13-1轴对称（第1课时）

- 1 - 13.1 轴对称 第 1 课时 教学目标 1．在生活实例中认识轴对称图． 2．分析轴对称图形，理解轴对称的概念． 教学重点： 轴对称图形的概念． 教学难点： 能够识别轴对称图形并找出它的对称轴． 教学过程 一、创设情境，引入新课 我们生活在一个充满对称的世界中，许多建筑物都设计成对称形，艺术作品的创作往往 也从对称角度考虑，自然界的许多动植物也按对称形生长，中国的方块字中些也具有对称 性……对称给我们带来多少美的感受！初步掌握对称的奥秒，不仅可以帮助我们发现一些图 形的特征，还可以使我们感受到自然界的美与和谐． 轴对称是对称中重要的一种，从这节课开始，我们来学习第十二章：轴对称．今天我们 来研究第一节，认识什么是轴对称图形，什么是对称轴． 二、导入新课 出示课本的图片，观察它们都有些什么共同特征． 这些图形都是对称的．这些图形从中间分开后，左右两部分能够完全重合． 小结：对称现象无处不在，从自然景观到分子结构，从建筑物到艺术作品，甚至日常生 活用品，人们都可以找到对称的例子．现在同学们就从我们生活周围的事物中来找一些具有 对称特征的例子． 我们的黑板、课桌、椅子等． 我们的身体，还有飞机、汽车、枫叶等都是对称的． 如课本的图 12．1．2，把一张纸对折，剪出一个图案（折痕处不要完全剪断），再打开 这张对折的纸，就剪出了美丽的窗花．观察得到的窗花和图 12．1．1 中的图形，你能发现 它们有什么共同的特点吗？ 窗花可以沿折痕对折，使折痕两旁的部分完全重合．不仅窗花可以沿一条直线对折，使 直线两旁重合，上面图 12．1．1 中的图形也可以沿一条直线对折，使直线两旁的部分重合． 结论：如果一个图形沿一直线折叠，直线两旁的部分能够互相重合，这个图形就叫做 轴对称图形，这条直线就是它的对称轴．这时，我们也说这个图形关于这条直线（成轴） 对称． 了解了轴对称图形及其对称轴的概念后，我们来做一做． 取一张质地较硬的纸，将纸对折，并用小刀在纸的中央随意刻出一个图案，将纸打开后 铺平，你得到两个成轴对称的图案了吗？与同伴进行交流． 结论：位于折痕两侧的图案是对称的，它们可以互相重合． 由此可以得到轴对称图形的特征：一个图形沿一条直线折叠后，折痕两侧的图形完全重 - 2 - 合． 接下来我们来探讨一个有关对称轴的问题．有些轴对称图形的对称轴只有一条，但有的 轴对称图形的对称轴却不止一条，有的轴对称图形的对称轴甚至有无数条。 下列各图，你能找出它们的对称轴吗？ 结果：图（1）有四条对称轴；图（2）有四条对称轴；图（3）有无数条对称轴；图（4） 有两条对称轴；图（5）有七条对称轴． (1) (2) (3) (4) (5) 展示挂图，大家想一想，你发现了什么？ 像这样，把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就 说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做 对称点． 三、随堂练习： - 3 - 课本 P60 练习 1、2. 四、课时小结 这节课我们主要认识了轴对称图形，了解了轴对称图形及有关概念，进一步探讨了轴对 称的特点，区分了轴对称图形和两个图形成轴对称． 五、作业：课本 P64 习题 13．1 第 1、2、6、7、8 题． 六、活动与探究：课本 P59 思考． 成轴对称的两个图形全等吗？如果把一个轴对称图形沿对称轴分成两个图形，那么这两 个图形全等吗？这两个图形对称吗？ 过程：在硬纸板上画两个成轴对称的图形，再用剪刀将这两个图形剪下来看是否重合．再 在硬纸板上画出一个轴对称图形，然后将该图形剪下来，再沿对称轴剪开，看两部分是否能 够完全重合． 结论：成轴对称的两个图形全等．如果把一个轴对称图形沿对称轴分成两个图形，这两 个图形全等，并且也是成轴对称的． 轴对称是说两个图形的位置关系，而轴对称图形是说一个具有特殊形状的图形． 轴对称的两个图形和轴对称图形，都要沿某一条直线折叠后重合；如果把轴对称图形沿 对称轴分成两部分，那么这两个图形就关于这条直线成轴对称；反过来，如果把两个成轴对 称的图形看成一个整体，那么它就是一个轴对称图形． 板书设计 §13.1.1 轴对称 一、轴对称：如果一个图形沿一条直线折叠后，直线两旁的部分能够完全重合，这个 图形就叫轴对称图形，这条直线叫对称轴． 二、两个图形成轴对称：把一个图形沿着某一条直线折叠，如果它能够与另一个图形 重合，那么就说这两个图形关于这条直线对称．