华师版数学八年级上册课件-第12章- 复习课

华师版数学八年级上册课件-第12章- 复习课

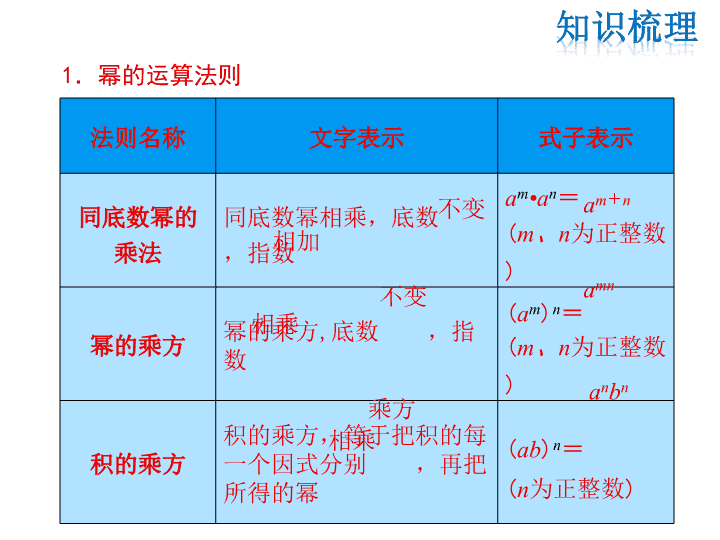
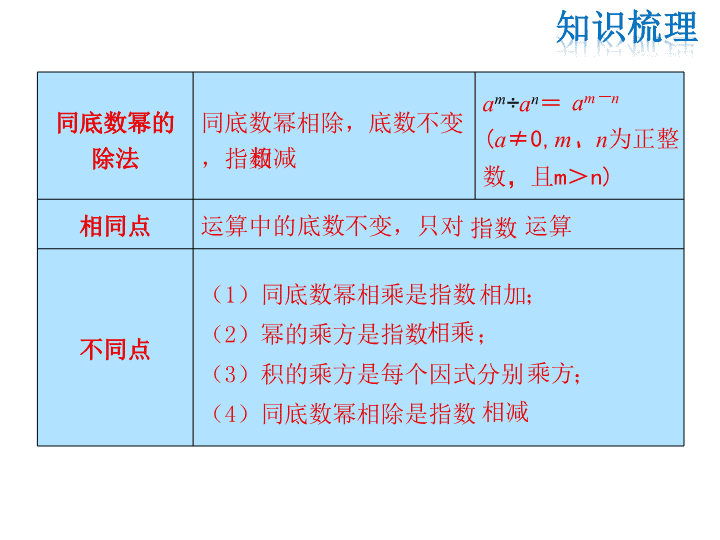
第12章 整式的乘除 复习课 1．幂的运算法则 法则名称 文字表示 式子表示 同底数幂的 乘法 同底数幂相乘，底数 ， 指数 am•an＝　 　 (m、n为正整数) 幂的乘方 幂的乘方,底数 ，指 数 (am)n＝　 　 (m、n为正整数) 积的乘方 积的乘方，等于把积的每 一个因式分别 ，再把 所得的幂 (ab)n＝　 　 (n为正整数) am＋n amn anbn　 不变 相乘 相加 不变 相乘 乘方 同底数幂的 除法 同底数幂相除，底数 ， 指数 am÷an＝ (a≠0,m、n为正 整数，且m＞n) 相同点 运算中的 不变，只对 运算 不同点 （1）同底数幂相乘是指数 ； （2）幂的乘方是指数 ； （3）积的乘方是每个因式分别 ； （4）同底数幂相除是指数 不变 相减 底数 指数 相加 相乘 乘方 相减 am－n 　注意：(1)其中的a、b代表的不仅可以是单独的数、 单独的字母，还可以是一个任意的代数式； (2)这几个法则容易混淆，计算时，必须先搞清楚 该不该用法则，该用哪个法则． 2．整式的乘法 单项式与单项式相乘，把它们的　 　、　 　分 别相乘，对于只在一个单项式中出现的字母，则连同它的指数 一起作为积的一个　 　. 单项式与多项式相乘，用　　 和　　 的每一项分别 相乘，再把所得的积　 　. 多项式与多项式相乘，先用一个多项式的　 　与另一 个多项式的　 　相乘，再把所得的积　 　. 系数 相同字母的幂 因式 单项式 多项式 相加 每一项 每一项 相加 3．乘法公式 公式名称 两数和乘以这两数的差 两数和(差)的平方 文字表示 两数和与这两数的差的积， 等于这两数的平方差 两数和(差)的平方，等 于这两数的　 　加 上(减去)　 　的 2倍 式子表示 (a＋b)(a－b)＝ (a±b)2＝　　 平方和 这两数积 a2－b2 a2±2ab＋b2 结构 特点 ①左边是两个　　项式相 乘，这两个二项式中有一 项　 　，另一项　 　； ②右边是　　项式，是乘 式中两项的　 　，即 相同项的平方与相反项的 平方的差 ①左边是一个　　项式的和 (或差)的　 　； ②右边是　　项式，是左边 二项式中两项的 　， 再 (或减去)它们　的 2倍 顺口 溜 和差积，平方差 首平方，尾平方，首尾　倍 中间放，加减看前方，同加 异减 二 完全相同 互为相反数 二 平方差 二 平方 三 平方和 加上 积 两 公式的常 用变形 a2＝　 　(a－b)＋b2； b2＝　　－(a＋b)(a－b) a2＋b2＝(a＋b)2－ ,　　 或(a－b)2＋ 　； (a＋b)2＝(a－b)2＋ 　 (a＋b) 2ab 2ab 4ab 注意：(1)乘法公式实际上是一种特殊形式的多项式的乘法， 公式的主要作用是简化运算. (2)公式中的字母可以表示数，也可以表示其他单项式或 多项式． a2 4．整式的除法 (1)单项式除以单项式 单项式相除，把　 　、　 　分别相除作为商的 　， 对于只在被除式中出现的字母，则连同它的指数一起作为商的一 个　 　. (2)多项式除以单项式 多项式除以单项式，先把这个多项式的每一项除以这个 　 ，再把所得的商　 　. 系数 同底数幂 因式 因式 单项式 相加 注意：多项式除以单项式实质上是用计算法则转化为单项 式除以单项式． 5．因式分解的意义 把一个多项式化成几个整式的　　的形式，叫做多项式的 因式分解．因式分解的过程和　 　的过程正好相反． 6．用提公因式法分解因式 公因式的确定：公因式的系数应取多项式各项整数系数 的　 ；字母取多项式各项　 　的字母；各字母 指数取次数最　　的． 一般地，如果多项式的各项都含有公因式，可以把这个 公因式提到　 　外面，将多项式写成　 　的形式， 这种分解因式的方法叫做提公因式法． 积 整式乘法 最大公约数 相同 低 括号 因式乘积 注意：提公因式法是因式分解的首选方法，在因式分解时 先要考虑多项式的各项有无公因式． 7．用公式法分解因式 把　 　反过来，可以把符合公式特点的多项式分解 因式，这种分解因式的方法叫做公式法．常用的两个公式是： (1)逆用平方差公式 ＝　 　； (2)逆用两数和(差)的平方公式 乘法公式 (a＋b)(a－b) ＝ . a2－b2 a2±2ab＋b2 (a±b)2 注意：这里的两个公式是用来分解因式的，与乘法公式 刚好左右互换．运用公式分解因式，首先要对所给的多项 式的项数、次数、系数和符号进行观察，判断符合哪个公 式的条件．公式中的字母可表示数、字母、单项式或多项 式，只有符合公式的特征时才能运用公式． 8．因式分解的步骤 (1)如果多项式的各项有公因式，那么先　 　； (2)在各项提出公因式后或各项没有公因式的情况下，观察 多项式的次数：二项式可以尝试运用　 　公式分解因式； 三项式可以尝试运用　 　公式分解因式； (3)分解因式必须分解到每一个因式在指定的范围内都不 能 　为止． 9．图形面积与代数恒等式 很多代数恒等式(如平方差公式、两数和(差)的平方公式 等)都可以用平面几何图形的　 　来说明其正确性，方法是 把图形的面积用不同的方式表示，根据列出的代数式　 　， 然后得到代数恒等式． 提取公因式 平方差 两数和(差)的 再分解 面积 相等 【例1】 计算： （1）(2a)3(b3)2÷4a3b4； （2）(-8)2018 ×0.1252017. 【解析】（1）幂的混合运算中，先算乘方，再算乘除； （2）可以先用同底数幂的乘法的逆运算，将 （-8）2018 化为（-8） ×（-8）2017，再用积的乘方的 性质的逆运算进行计算. 解：（1）原式=8a3b6 ÷4a3b4=2a3-3b6-4=2b2. （2）原式=（-8）×（-8）2017 ×0.1252017 =（-8）×[（-8） ×0.125]2017 =（-8）×（-1）2017=8. 1 1.下列计算不正确的是（ ） A.2a3÷a=2a2 B. (-a3)2=a6 C. a4 ·a3=a7 D. a2 ·a4=a8 D 【归纳总结】 幂的运算性质包括同底数幂的乘法、幂的 乘方、积的乘方及同底数幂的除法.这四种运算性质贯穿全 章，是整式乘除及因式分解的基础.其逆向运用可将问题化 繁为简，负数乘方结果的符号，奇次方得负，偶次方得正. 2. 计算：0.252017 ×（-4）2017-8100 ×0.5301. 解：原式=[0.25 ×（-4）]2017-（23）100 ×0.5300 ×0.5 =-1-（2 ×0.5）300 ×0.5 =-1-0.5 =-1.5. 解：∵420=（42）10=1610， 1610>1510, ∴420>1510. 3. 比较大小：420与1510. 【例2】 计算：[x(x2y2-xy)-y(x2-x3y)] ÷3x2y,其中x=1,y=3. 【解析】计算整式的加、减、乘、除、乘方的运算时，一要注 意运算顺序；二要熟练、正确地运用运算法则. 解：原式=(x3y2-x2y-x2y+x3y2) ÷3x2y =(2x3y2-2x2y) ÷3x2y = .2 2 3 3 x y 当x=1,y=3时，原式= .2 2 2 2 41 33 3 3 3 3      x y 2 【归纳总结】整式的乘除法主要包括单项式乘以单项 式、单项式乘以多项式、多项式乘以多项式以及单项式除 以单项式、多项式除以单项式，其中单项式乘以单项式是 整式乘除的基础，必须熟练掌握它们的运算法则. 整式的混合运算要按照先乘方，再乘除，最后加减的 顺序进行，有括号的要先算括号里的. 4.一个长方形的面积是a2-2ab+a，宽为a，则长方形的长 为 . 5.已知多项式2x3-4x2-x除以一个多项式A，得商为2x，则 这个多项式是 . a2-2b+1 2 2 1 x x 【例3】 先化简，再求值：[(x-y)2+(x+y)(x-y)] ÷2x，其中 x=3，y=1.5. 【解析】运用平方差公式和完全平方公式，先算括号内的，再 进行整式的除法运算. 解：原式=(x2-2xy+y2+x2-y2) ÷2x =(2x2-2xy) ÷2x =x-y. 当x=3，y=1.5时，原式=3-1.5=1.5. 3 【归纳总结】整式的乘法公式包括平方差公式和完全 平方公式，而完全平方公式又分为两个：两数和的完全平 方公式和两数差的完全平方公式，在计算多项式的乘法时， 对于符合这三个公式结构特征的式子，运用公式可减少运 算量，提高解题速度. 6.求方程(x-1)2-(x-1)(x+1)+3(1-x)=0的解. 解：∵x2+9y2+4x-6y+5=0, ∴(x2+4x+4)+(9y2-6y+1)=0， ∴(x+2)2+(3y-1)2=0. ∴x+2=0，3y-1=0，解得x=-2, y= , ∴ 7.已知x2+9y2+4x-6y+5=0,求xy的值. 解：原方程可化为-5x+5=0，解得x=1. 1 3 1 2( 2 ) .3 3x y      【例4 】 判断下列各式变形是不是分解因式，并说明理由： (1)a2-4+3a=(a+2)(a-2)+3a; (2)(a+2)(a-5)=a2-3a-10; (3)x2-6x+9=(x-3)2; (4)3x2-2xy+x=x(3x-2y)2. 解：（1）不是.理由：最后不是做乘法运算，不是积的形式. （2）不是.理由：从左到右是做乘法运算. （3）是. （4）不是.理由：3x2-2xy+x=x(3x-2y+1). 【解析】（1）因式分解的定义包括两点：一是等式的左边是一 个多项式；二是等式的右边要化成几个整式乘积的形 式，即等式的整个右边化成积的形式； （2）判断过程要从左到右保持恒等变形. 4 【归纳总结】因式分解是把一个多项式化成几个整式的 积的形式，它与整式乘法互为逆运算. 分解因式的方法主要是提公因式法和公式法.因式分解 时，一般先提公因式，再用公式法分解，因式分解要求分 解到每一个因式都不能再分解为止. 8.下列变形，是因式分解的是（ ） A. a(x+y)=ax+ay B. x2+4xy+y2-1=x(x+4y)+(y+1)(y-1) C. am2-a=a(m+1)(m-1) D. m2-9n2+3=(m+3n)(m-3n)+3 C 【例5 】计算：(1)-2a·3a2b3· ( ; (2)（-2x+5+x2）·（-6x3）.2 5 bc    【解析】(1)单项式乘以单项式可以转化为有理数的乘法和同 底数幂的乘法； (2)多项式乘以单项式可以转化为单项式乘以单项式. 解：（1）原式= 1 2 3 1 3 42 122 3 .5 5a b c a b c         （2）原式=（-2x）·（-6x3）+5·（-6x3）+x2·（-6x3） =12x4-30x3-6x5. 5 【归纳总结】将要解决的问题转化为另一个较易解决的问 题，这是初中数学中常用的思想方法.如本章中，多项式× 多项式 单项式×多项式 单项式×单项式 有理数的 乘法和同底数幂的乘法.  转化  转化  转化 9.计算：（4a-b）•（-2b）2．. 解： 原式=（4a-b）•4b2=16ab2-4b3． 【例6】 若2a+5b-3=0，则4a·32b= . 【解析】由2a+5b-3=0，无法求出a，b的值，因此可以逆用积 的乘方先把4a·32b化简为含有与已知条件相关的部分， 即4a·32b=22a·25b=22a+5b.把2a+5b看作一个整体，因为 2a+5b-3=0，所以2a+5b=3，所以4a·32b=23=8. 8 【归纳总结】在本章中，应用幂的运算法则、乘法公式时， 可以将一个代数式看作一个字母，这就是整体思想，应用这 种思想方法解题，可以简化计算过程，且不易出错. 10.若xn=5，则（x3n）2-5（x2）2n= .12 500 11.若x+y=2，则 = .2 21 1 2 2x xy y  2 【例7】 如图所示，在边长为a的正方形中剪去边长为b 的小正方形，把剩下的部分拼成梯形，分别计算这两个图 形的阴影部分的面积，可验证的公式是 . b a a a a b b b b b a-b a2-b2=(a+b)(a-b) 【归纳总结】本章中，数形结合思想主要体现在根据给定 的图形写出一个代数恒等式或根据代数式画出几何图形. 由 几何图形得到代数恒等式时，需要用不同的方法表示几何图 形的面积，然后得出代数恒等式；由代数恒等式画图时，关 键在于合理拼接，往往是相等的边拼到一起． 12.我们已知道完全平方公式可以用平面几何图形的面积来表 示，实际上还有一个代数恒等式也可以用这种形式来表示，如 （2a+b)(a+b)=2a2+3ab+b2，就可以用图①和图②等图形的面积 表示. a a a b b ab ab aba2 a2 b2 图① b2 a2 a2 ab ab ab a a a b b图② （2）请画一个几何图形，使它的面积能表示 （a+b)(a+3b)=a2+4ab+3b2. （1）请写出图③所表示的代数恒等式； b ba a b a ab ab ab ab ab a2 a2 b2 b2 图③ 解：(1) (2a+b)(a+2b)=2a2+5ab+2b2. (2)如图④. 图④ a2 b a abab ab ab b2 b2b2 13.图①是一个长为2a，宽为2b的长方形，沿图中虚线剪开， 可分成四块小长方形． (1)求出图①的长方形面积； (2)将四块小长方形拼成如图②所示的正方形，利用阴影部 分面积的不同表示方法，直接写出代数式(a＋b)2、(a－b)2、 ab之间的等量关系． 解：(1)(a＋a)(b＋b)＝4ab. (2)(a＋b)2＝(a－b)2＋4ab. 幂的运算 乘法公式 整式的乘除 积的乘方 平方差公式 多项式与单项式相乘、相除 完全平方公式 整式的乘 除法 单项式与单项式相乘、相除 多项式与多项式相乘 同底数幂相乘 幂的乘方 同底数幂相除 因式分解 提公因式法 公式法