- 2021-10-27 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三角形的中位线学案
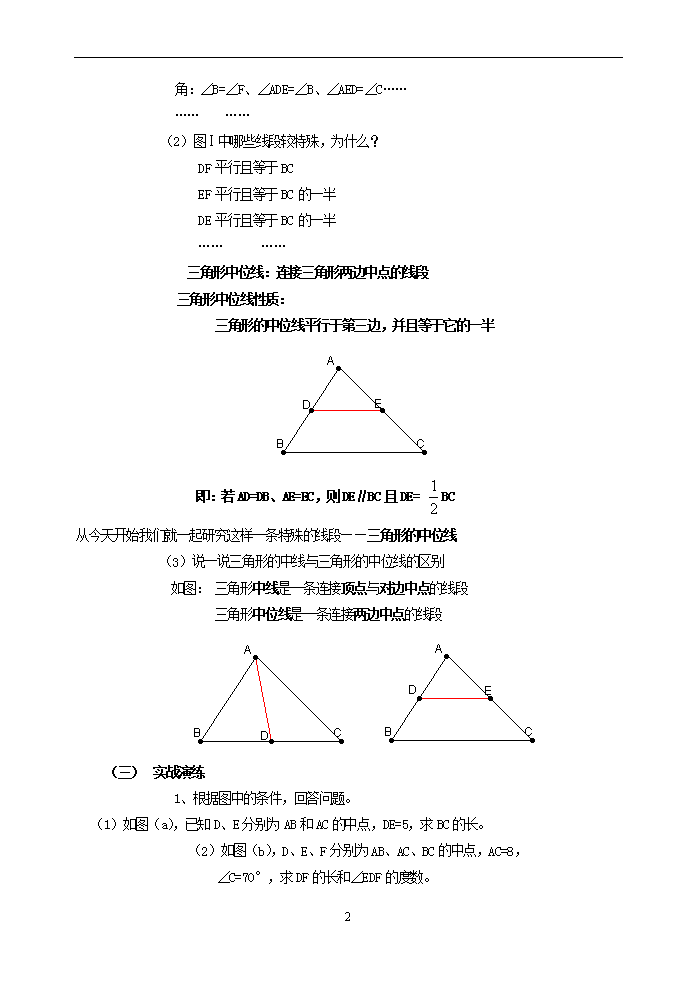
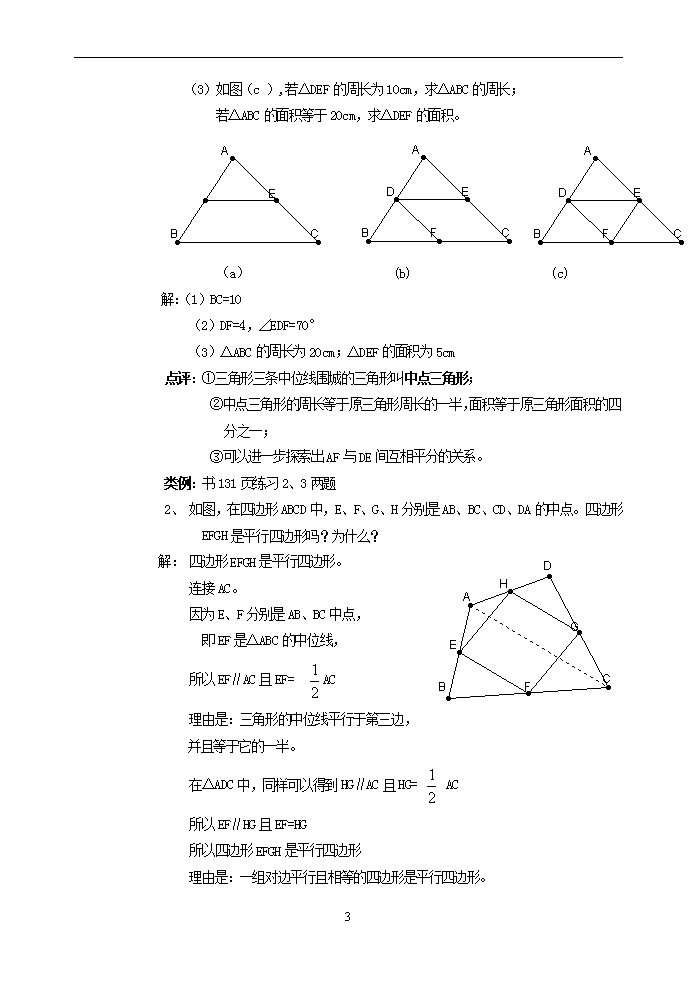
3.6 三角形的中位线 班级 姓名 学号 学习目标 1. 探索并掌握三角形的中位线的概念、性质 2. 会利用三角形中位线的性质解决有关问题 3. 经历探索三角形中位线性质的探索过程,发展学生观察能力及抽象思维能力 学习难点 利用三角形中位线性质解决有关问题 教学过程 (一) 情景创设 怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形? (二) 探索活动,引入新课 1、 动手操作 (1) 剪一个三角形记为△ABC; (2) 分别取AB、AC的中点D、E,连接DE; (3) 沿DE将△ABC剪成两部分, 将△ADE绕点E旋转180°,得四边形BCFD,如图Ⅰ (Ⅰ) 2、 观察思考 (1)图Ⅰ中有哪性质 ① 四边形BCFD是平行四边形吗?请说明理由。 ② 从边上考虑?从角上考虑? …… …… 观察探索得出: 边:AD=BD、AE=EC、DE=EF、BD=CF、DF=BC DF∥BC、DE∥BC、EF∥BC 6 角:∠B=∠F、∠ADE=∠B、∠AED=∠C…… …… …… (2)图Ⅰ中哪些线段较特殊,为什么? DF平行且等于BC EF平行且等于BC的一半 DE平行且等于BC的一半 …… …… 三角形中位线:连接三角形两边中点的线段 三角形中位线性质: 三角形的中位线平行于第三边,并且等于它的一半 即:若AD=DB、AE=EC,则DE∥BC且DE= BC 从今天开始我们就一起研究这样一条特殊的线段——三角形的中位线 (3)说一说三角形的中线与三角形的中位线的区别 如图: 三角形中线是一条连接顶点与对边中点的线段 三角形中位线是一条连接两边中点的线段 (一) 实战演练 1、根据图中的条件,回答问题。 (1)如图(a),已知D、E分别为AB和AC的中点,DE=5,求BC的长。 (2)如图(b),D、E、F分别为AB、AC、BC的中点,AC=8, ∠C=70°,求DF的长和∠EDF的度数。 6 (3)如图(c ),若△DEF的周长为10cm,求△ABC的周长; 若△ABC的面积等于20cm,求△DEF的面积。 (a) (b) (c) 解:(1)BC=10 (2)DF=4,∠EDF=70° (3)△ABC的周长为20cm;△DEF的面积为5cm 点评:①三角形三条中位线围城的三角形叫中点三角形; ②中点三角形的周长等于原三角形周长的一半,面积等于原三角形面积的四分之一; ③可以进一步探索出AF与DE间互相平分的关系。 类例:书131页练习2、3两题 2、 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么? 解: 四边形EFGH是平行四边形。 连接AC。 因为E、F分别是AB、BC中点, 即EF是△ABC的中位线, 所以EF∥AC且EF= AC 理由是:三角形的中位线平行于第三边,并且等于它的一半。 在△ADC中,同样可以得到HG∥AC且HG= AC 所以EF∥HG且EF=HG 所以四边形EFGH是平行四边形 理由是:一组对边平行且相等的四边形是平行四边形。 6 点评:①通过连接对角线将四边形中的问题转化到三角形中(未知转化为已知) ②次连接四边形各边中点的四边形是中点四边形; ③可以进一步探索中点四边形形状的特殊性与原四边形的对角线有关: 对角线相等的四边形的中点四边形为菱形; 对角线垂直的四边形的中点四边形为矩形。 (一) 课时小结 通过今天的学习,同学们有何收获和体会。 (1) 学习了三角形中位线的性质; (2) 利用三角形中位线的概念和性质解决有关问题; (3) 经历了探索三角形中位线性质的过程,体会转化的思想方法。 (二) 课后作业 课本134页1、3、4 【课后作业】 班级 姓名 学号 1、顺次连结矩形四边的中点所得的四边形是( ) A.矩形 B.菱形 C.正方形 D.以上都不对 2、如果四边形的对角线互相垂直,那么顺次连结四边形中点所得的四边形是( ) A.矩形 B.菱形 C.正方形 D.以上都不对 3、如果顺次连结四边形各边中点组成的四边形是菱形,那么原来的四边形的对角线( ) A.互相平分 B.互相垂直 C.相等 D.相等且互相平分 4、顺次连结下列各四边形中点所得的四边形是矩形的是( ). A.等腰梯形 B.矩形 C.平行四边形 D.菱形或对角线互相垂直的四边形 5、已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是( ). A.3cm B.26cm C.24cm D.65cm 6、已知以一个三角形各边中点为顶点的三角形的周长为8cm,则原三角形的周长为 cm 7、一个三角形的周长是12cm,则这个三角形各边中点围成的三角形的周长 . 8、如图△ABC中,D、E分别是AB、AC的中点,则线段CD是△ABC的___,线段DE是△ABC_______ 9、如图,D、E、F分别是△ABC各边的中点,(1)如果EF=4cm,那么BC=__cm;如果AB=10cm,那么DF=___cm;(2)中线AD与中位线EF的关系是___ 6 10、已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E、F是BC的中点,试说明BD=2EF。 11、如图,四边形ABCD中,AB=CD,M、N分别是AD、BC的中点,延长BA、NM、CD分别交于点E、F。 试说明∠BEN=∠NFC. 12、如图,A、B两地被建筑物阻隔,为测量A、B两地的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E. (1)若DE的长度为36米,求A、B两地之间的距离; (2)如果D、E两点之间还有阻隔,你有什么方法解决? 13、如图,矩形ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、DO的中点,四边形EFGH是矩形吗?为什么? 6 14、已知在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点. 求证:DM=AB 15、如图,在平行四边形ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H,试说明GH∥AD且GH=AD 6查看更多