北师大版数学八年级上册《蚂蚁怎样走最近》练习

北师大版数学八年级上册《蚂蚁怎样走最近》练习

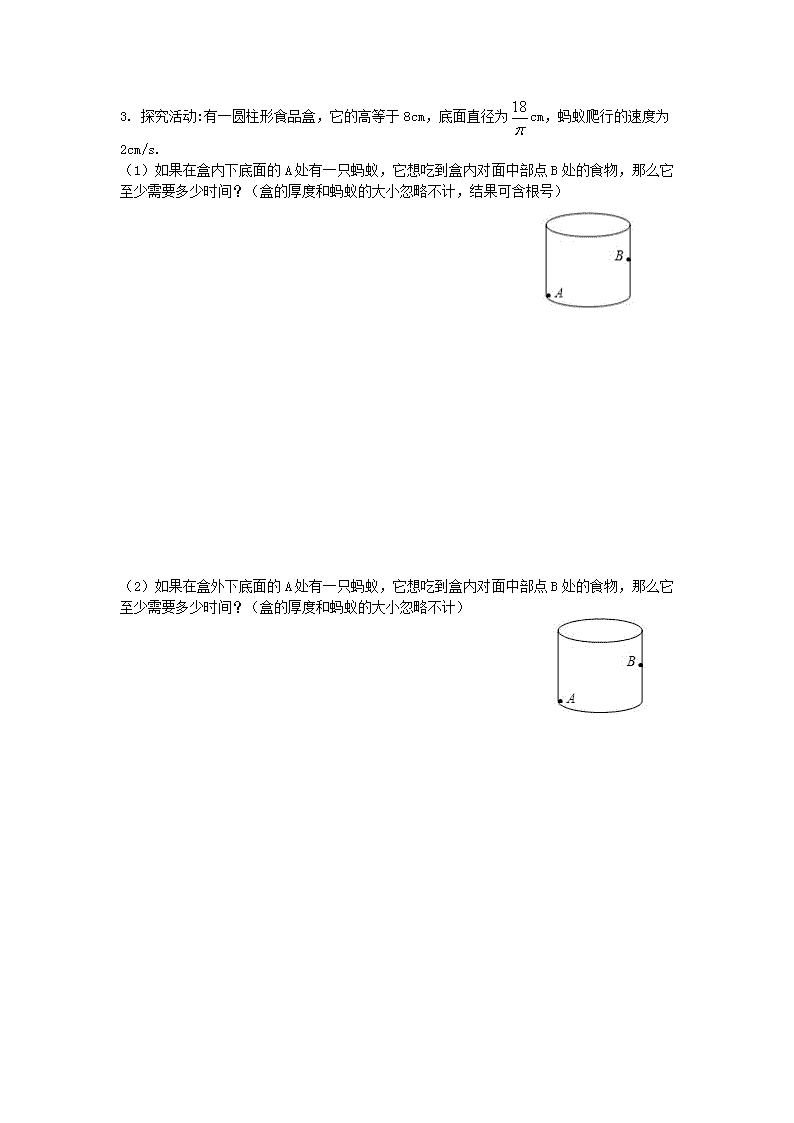
1.3 蚂蚁怎样走最近 专题 最短路径的探究 1. 编制一个底面周长为 a、高为 b 的圆柱形花柱架，需用沿圆柱 表面绕织一周的竹条若干根，如图中的 A1C1B1，A2C2B2，…，则 每一根这样的竹条的长度最少是______________. 2. 请阅读下列材料： 问题：如图（1），一圆柱的底面半径和高均为 5dm，BC 是底面 直径，求一只蚂蚁从 A 点出发沿圆柱表面爬行到点 C 的最短路线. 小明设计了两条路线： 路线 1：侧面展开图中的线段 AC.如下图（2）所示： 设路线 1 的长度为 1l ，则 2222222 1 2525)5(5  BCABACl ； 路线 2：高线 AB + 底面直径 BC，如上图（1）所示， 设路线 2 的长度为 2l ， 则 225)105()( 222 2  BCABl . 0)8(25200252252525 2222 2 2 1  ll . ∴ 2 2 2 1 ll  ∴ 21 ll  所以要选择路线 2 较短。 （1）小明对上述结论有些疑惑，于是他把条件改成：“圆柱的 底面半径为 1dm，高 AB 为 5dm”继续按前面的方式进行计算. 请你帮小明完成下面的计算： 路线 1：  22 1 ACl ___________________； 路线 2：  22 2 )( BCABl __________ , ∵ 2 2 2 1 _____ ll , ∴ 21 _____ ll ( 填>或<). 所以应选择路线____________(填 1 或 2)较短. (2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为 r,高为 h 时，应如何选择上面 的两条路线才能使蚂蚁从点 A 出发沿圆柱表面爬行到 C 点的路线最短. 比较两个正数的大 小，有时用它们的 平方来比较更方便 3. 探究活动:有一圆柱形食品盒，它的高等于 8cm，底面直径为18  cm，蚂蚁爬行的速度为 2cm/s. （1）如果在盒内下底面的 A 处有一只蚂蚁，它想吃到盒内对面中部点 B 处的食物，那么它 至少需要多少时间？（盒的厚度和蚂蚁的大小忽略不计，结果可含根号） （2）如果在盒外下底面的 A 处有一只蚂蚁，它想吃到盒内对面中部点 B 处的食物，那么它 至少需要多少时间？（盒的厚度和蚂蚁的大小忽略不计） 答案： 1. 2 2a b 【解析】 底面周长为 a、高为 b 的圆柱的侧面展开图为矩形,它的边长分别 为 a,b，所以对角线长为 2 2a b ，所以每一根这样的竹条的长度最少是 2 2a b . 2.解：（1）25+π2 49 ＜ ＜ 1 （2）l1 2=AC2 =AB2+BC2=h2+（πr）2， l2 2=（AB+BC）2=（h+2r）2， l1 2-l2 2=h2+（πr）2-（h+2r）2=r（π2r-4r-4h）=r[（π2-4）r-4h]. r 恒大于 0，只需看后面的式子即可． 当 r= 2 4 4 h   时，l1 2=l2 2； 当 r＞ 2 4 4 h   时，l1 2＞l2 2； 当 r＜ 2 4 4 h   时，l1 2 ＜l2 2． 3. 解 ： （ 1 ） 如 图 ， AC=π• 18  ÷2=9cm ， BC=4cm ， 则 蚂 蚁 走 过 的 最 短 路 径 为 ： AB= 2 29 4 = 97 cm，所以 97 ÷2= 97 2 （s），即至少需要 97 2 s． （2）如图，作 B 关于 EF 的对称点 D，连接 AD，交 EF 于点 P，连接 BP，则 蚂蚁走的最短路程是 AP+PB=AD，由图可知，AC=9cm，CD=8+4=12（cm）． 所以 AD= 2 29 12 =15（cm），15÷2=7.5（s） 即至少需要 7.5s．