八年级下册数学同步练习第十八章复习2 人教版

八年级下册数学同步练习第十八章复习2 人教版

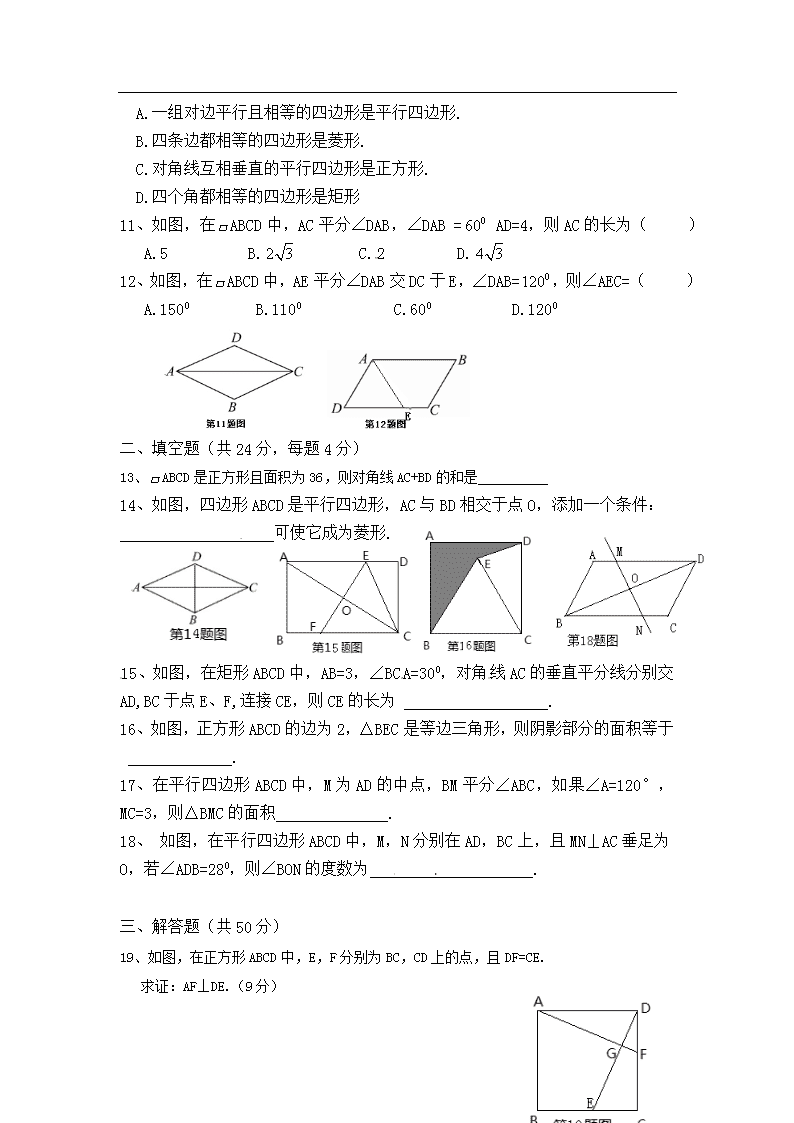
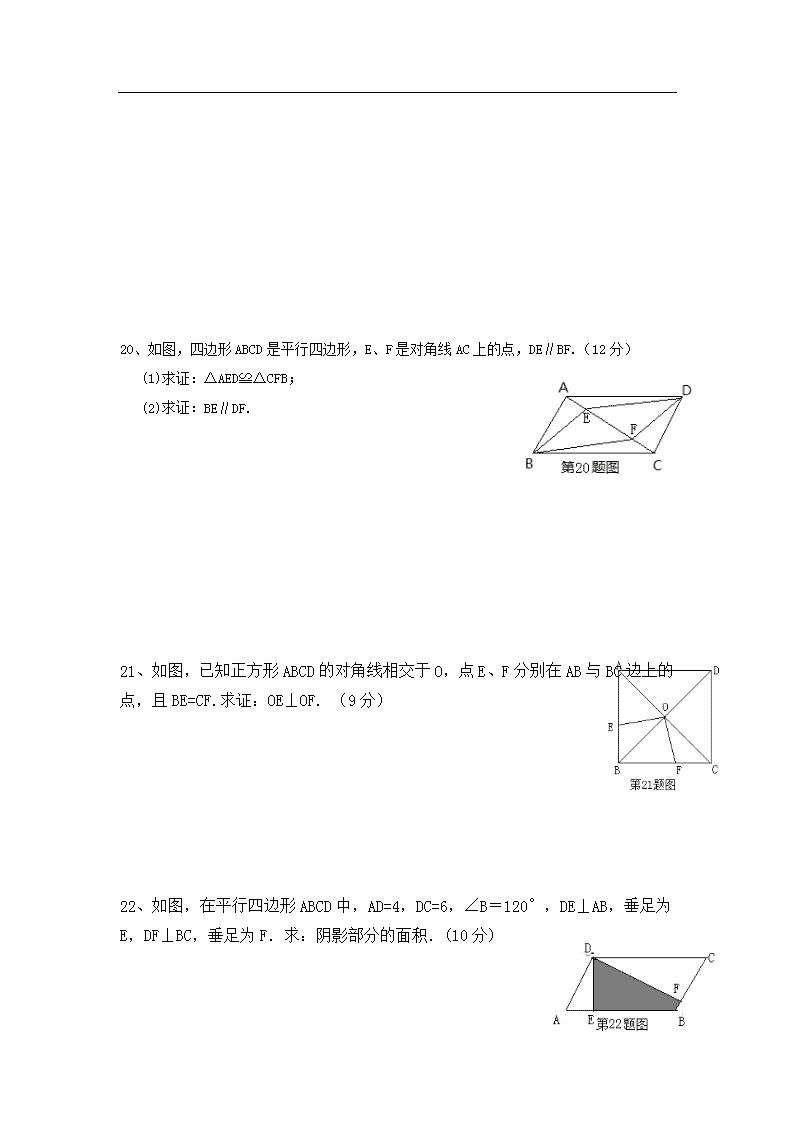
‎《平行四边形》复习 一、选择题（共36分，每题3分）‎ ‎1、下面各条件中，能判定四边形是平行四边形的是  （   ）‎ ‎ A、对角线互相垂直  B、两组对边分别相等 ‎ C、一组对角相等  D、一组对边相等 ，另一组对边平行 ‎2、正方形具有而矩形不具有的性质是   (   ) ‎ A．对角线互相垂直    B．对角相等 C．对角线互相平分   D．四角相等 ‎3、已知ABCD是平行四边形，下列结论中正确的是①AB∥CD ②AC=BD ③当AC=BD是，它是菱形 ④当∠ABC=900时，它是矩形 （ ）‎ A. ①② B.①④ C. ②③ D.③④‎ ‎4、若菱形的对角线分别为6和 8，则菱形的周长是 （ ）‎ A. 24 B.14 C.10 D.20‎ ‎5、在ABCD中，对角线AC与BD相交于点O,ΔBOC的周长为27cm，BC=12则AC+BD的长是 （   ） ‎ A.13cm    B.15cm     C. 30cm     D. 7cm ‎6、如图，在平行四边形ABCD中，∠A+∠C=1000，则 = (   )‎ A. B. C. D.‎ ‎7、如图，在菱形ABCD中, 延长AB于E并且 CE⊥AE,AC=2CE,则∠BCE的度数为（ ）‎ A． B. C. D. [来源:Zxxk.Com]‎ ‎8、如图所示，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点．若△ABC的周长为10，则△OEC的周长为 (   ) ‎ ‎ A．5cm     B．6cm     C．9cm    D．12cm ‎9、如图，把矩形ABCD沿AE对折后点B落在AC上，若=1500，则∠EAC=（   ） ‎ A．45°   B．60°  C．15°   D．30°‎ ‎10、下列说法错误的是（  ）  ‎ A.一组对边平行且相等的四边形是平行四边形.‎ B.四条边都相等的四边形是菱形.      ‎ C.对角线互相垂直的平行四边形是正方形.     ‎ D.四个角都相等的四边形是矩形 ‎11、如图，在ABCD中，AC平分∠DAB，∠DAB = AD=4，则AC的长为（ ）‎ A.5 B. C.2 D.‎ ‎12、如图，在ABCD中，AE平分∠DAB交DC于E，∠DAB=，则∠AEC=（ ）‎ A.1500 B.1100 C.600 D.1200‎ 二、填空题（共24分，每题4分）‎ ‎13、ABCD是正方形且面积为36，则对角线AC+BD的和是 ‎ ‎14、如图，四边形ABCD是平行四边形，AC与BD相交于点O，添加一个条件：‎ ‎ 可使它成为菱形.‎ ‎[来源:学.科.网]‎ ‎15、如图，在矩形ABCD中，AB=3，∠BCA=300，对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE，则CE的长为 .‎ ‎16、如图，正方形ABCD的边为2，△BEC是等边三角形，则阴影部分的面积等于 ‎ .‎ ‎17、在平行四边形ABCD中，M为AD的中点，BM平分∠ABC，如果∠A=120°，MC=3，则△BMC的面积 .‎ ‎18、 如图，在平行四边形ABCD中，M，N分别在AD，BC上，且MN⊥AC垂足为O，若∠ADB=280，则∠BON的度数为 .‎ 三、解答题（共50分）‎ ‎19、如图，在正方形ABCD中，E，F分别为BC，CD上的点，且DF=CE.‎ 求证：AF⊥DE.（9分）‎ ‎20、如图，四边形ABCD是平行四边形，E、F是对角线AC上的点，DE∥BF.（12分）‎ ‎(1)求证：△AED≌△CFB；‎ ‎(2)求证：BE∥DF.‎ ‎21、如图，已知正方形ABCD的对角线相交于O，点E、F分别在AB与BC边上的点，且BE=CF.求证：OE⊥OF. （9分）‎ ‎22、如图，在平行四边形ABCD中，AD=4，DC=6，∠B＝120°，DE⊥AB，垂足为E，DF⊥BC，垂足为F．求：阴影部分的面积．(10分)‎ ‎23、如图，在平行四边形ABCD中，∠ABC=600，E、F分别在CD和BC的延长线上，[来源:Zxxk.Com]‎ AE∥BD,EF⊥BC, AG⊥BC,EF=.（10分）‎ 求：AG的长.‎ 一、选择题（共36分，每题3分）‎ ‎1—5 BABDC 6—10 ACACC 11—12 DD 二、填空题（共24分，每题4分）‎ ‎13. 14.AB=AD(或AC⊥BD) 15. 16. 17. ‎ ‎18. 620[来源:学§科§网]‎ 三、解答题（共50分）‎ ‎19.（9分）‎ 证明：∵四边形ABCD是正方形 ‎∴AD=DC ∠ADF=∠DCE=900‎ 又DF=CE ‎∴△ADF≌△DCE ‎∴∠AFD=∠DEC ‎∵∠AFD+∠CDE=∠AGD ，∠DEC+∠CDE=900‎ ‎∴∠AGD=900‎ ‎∴AF⊥DE.‎ ‎20.（12分）‎ 证明：（1）∵四边形ABCD是平行四边形 ‎∴∠DAE=∠BCF, AD=C[来源:学科网ZXXK]‎ ‎∵DE∥BF ‎∴∠DEF=∠BFE ‎∵∠DAE+∠ADE=∠DEF, ∠BCF+∠CBF=∠BFE ‎∴∠ADE=∠CBF ‎∴△AED≌△CFB ‎(2)由△AED≌△CFB可知DE=BF 又DE∥BF ‎∴四边形BEDF边形 ‎∴BE∥DF.‎ ‎21.（9分）‎ 证明：∵四边形ABCD是正方形 ‎∴OB=OC , ∠OBE=∠OCF=450 , AC⊥BD ‎∵BE=CF ‎∴△OBE≌△OCF ‎∴∠EOB=∠FOC ‎∵AC⊥BD ‎∴∠BOC=900‎ ‎∵∠EOB+∠BOF=∠EOF , ∠FOC+∠BOF=∠BOC=900‎ ‎∴∠EOF=∠BOC=900‎ ‎∴OE⊥OF.‎ ‎22.（10分）‎ 解：∵四边形ABCD是平行四边形，∠B＝120°‎ ‎∴∠A=600 ∠C=600 ∠ADC=1200‎ 在△AED中∵DE⊥AB , ∠A=60‎ ‎∴∠ADE=300‎ ‎∴AE==‎ ‎∴DE=‎ 在△DFC中∵DF⊥BC ，∠C=600‎ ‎ ∴∠FDC=300‎ ‎∴‎ ‎∴‎ ‎ ‎ ‎23.（10分）‎ 解：∵四边形ABCD是平行四边形 ‎∴AB∥CD ‎∴∠DCE=∠ABC=600‎ 在△ECF中∵ AG⊥BC ‎ ‎, ∠CEF=300 ‎ ‎∴CE=2CF ‎ 又 CE= ，EF=‎ ‎∴ CE=2‎ ‎∵AE∥BD AB∥CE ‎∴四边形ABDE是平行四边形 ‎∴AB=DE ‎∴AB= = =1‎ 在△AEB中，∵AG⊥BC ‎∴∠BAE=300‎ ‎∴BE= ‎ ‎∴‎