- 2021-10-26 发布 |
- 37.5 KB |
- 4页

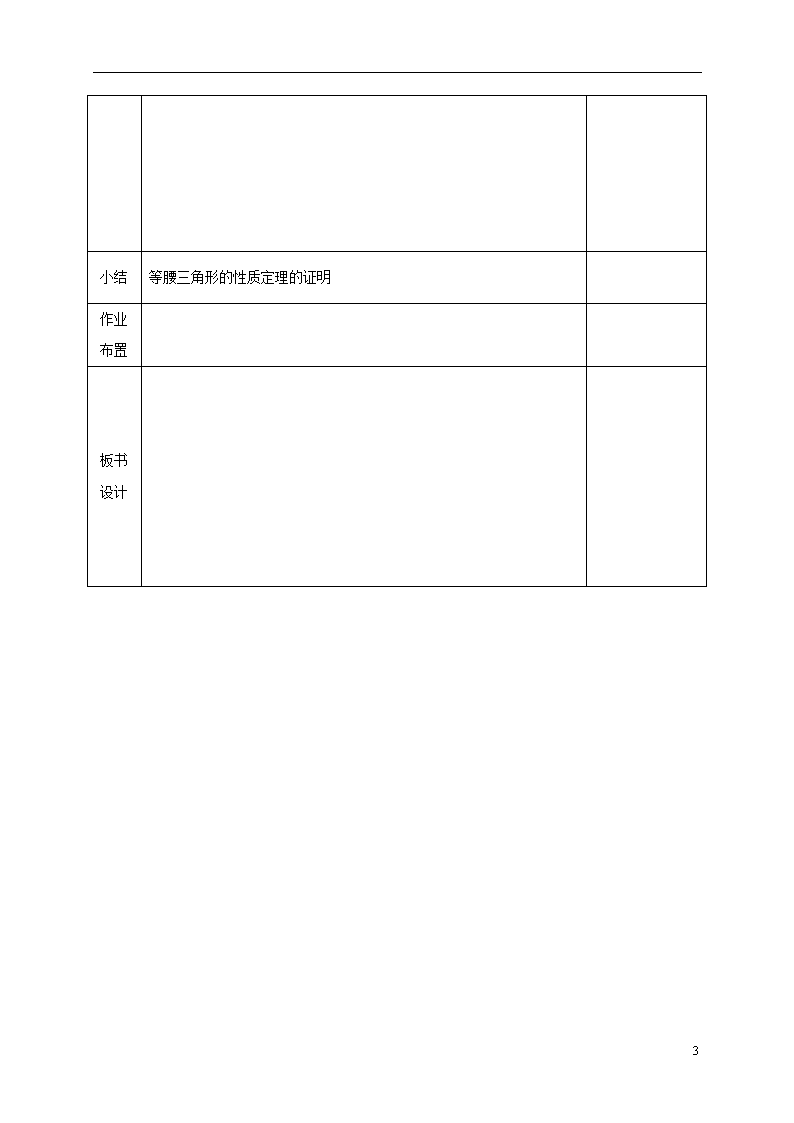
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020八年级数学下册 第1章 三角形的证明 第1节 等腰三角形(1)教案 (新版)北师大版
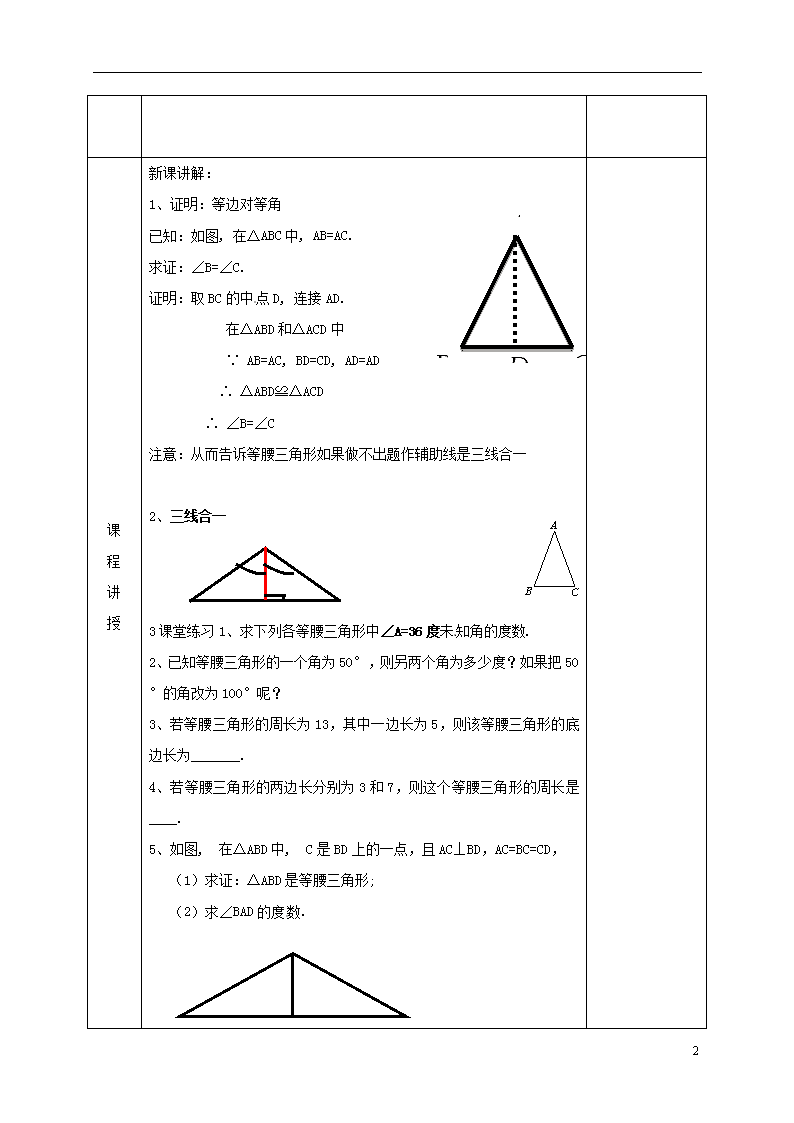
1.1等腰三角形 课题 1.1等腰三角形(1) 课型 讲授课 教学目标 1、 理解作为证明基础的几条公理的内容,应用这些公理证明等腰三角形的性质定理; 2、经历“探索-发现-猜想-证明”的过程,让学生进一步体会证明是探索活动的自然延续和必要发展,发展学生的初步的演绎逻辑推理的能力 3、启发引导学生体会探索结论和证明结论,及合情推理与演绎的相互依赖和相互补充的辩证关系 重点 探索证明等腰三角形性质定理的思路与方法,掌握证明的基本要求和方法; 难点 明确推理证明的基本要求如明确条件和结论,能否用数学语言正确表达等。 教学用具 多媒体课件 教学环节 复习 复习引入: 1.三角形全等的判定: 两边及其夹角对应相等的两个三角形全等; (SAS) 两角及其夹边对应相等的两个三角形全等; (ASA) 三边对应相等的两个三角形全等. (SSS) 两角及其中一角的对边对应相等的两个三角形全等(AAS) 2.全等三角形的性质: 全等三角形的对应边相等,对应角相等. 3.等腰三角形的性质 等腰三角形的两个底角相等 等腰三角形的两腰相等 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一). 4.等腰三角形是轴对称图形 4 课 程 讲 授 新课讲解: 1、证明:等边对等角 已知:如图, 在△ABC中, AB=AC. 求证:∠B=∠C. 证明:取BC的中点D, 连接AD. 在△ABD和△ACD中 C B A D ∵ AB=AC, BD=CD, AD=AD ∴ △ABD≌△ACD ∴ ∠B=∠C 注意:从而告诉等腰三角形如果做不出题作辅助线是三线合一 2、三线合一 A C B D 1 2 3课堂练习1、求下列各等腰三角形中∠A=36度未知角的度数. 2、已知等腰三角形的一个角为50°,则另两个角为多少度?如果把50°的角改为100°呢? 3、若等腰三角形的周长为13,其中一边长为5,则该等腰三角形的底边长为_______. 4、若等腰三角形的两边长分别为3和7,则这个等腰三角形的周长是 ____. 5、如图, 在△ABD中, C是BD上的一点,且AC⊥BD,AC=BC=CD, (1)求证:△ABD是等腰三角形; (2)求∠BAD的度数. A B D C 4 小结 等腰三角形的性质定理的证明 作业布置 板书设计 4 课后反思 4查看更多