- 2021-10-26 发布 |
- 37.5 KB |
- 24页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版数学八年级上册同步练习课件-第13章-13三角形全等的判定
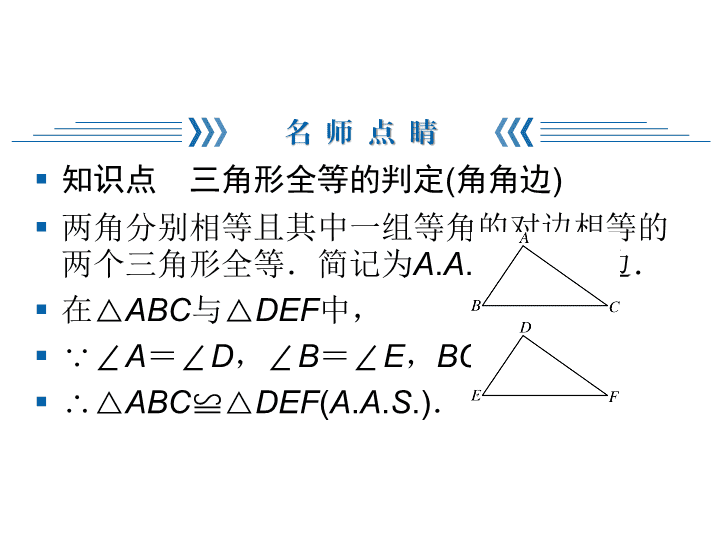
第13章 全等三角形 4 角边角(2)(第四课时) § 知识点 三角形全等的判定(角角边) § 两角分别相等且其中一组等角的对边相等的 两个三角形全等.简记为A.A.S.或角角边. § 在△ABC与△DEF中, § ∵∠A=∠D,∠B=∠E,BC=EF, § ∴△ABC≌ △DEF(A.A.S.). 2 § 注意:(1)要证两条线段相等或两个角相等, 我们可以证明它们所在的两个三角形全等, 从而利用全等三角形的性质得到结论. § (2)由三角形的内角和定理知,只要两个三角 形的两个角分别相等,则其第三个角也相等, 所以两角及一边分别相等的两个三角形一定 全等.即无论这一边是“对边”还是“夹 边”,只要相等即可判定两个三角形全等. 3 § 【典例】如图,点B、E、C、F在同一直线 上,AB=DE,∠A=∠D,AC∥DF.求证: △ABC≌ △DEF. § 分析:首先根据AC∥DF可得∠ACB=∠F, 再由A.A.S.即可证明△ABC≌△DEF. 4 § 点评:无论是“角边角”还是“角角边”, 都要找出两组角和一组边相等. 5 § 1.在△ABC和△A′B′C′中,已知AB=A′B′, ∠A=∠A′,∠C=∠C′,直接判定 △ABC≌ △A′B′C′的根据是 ( ) § A.S.S.S. B.A.S.A. § C.A.A.S. D.S.A.S. § 2.根据下列已知条件,能画出唯一△ABC 的是 ( ) § A.AB=5,BC=3,AC=8 B.AB=4, BC=3,∠A=30° § C.∠C=90°,AB=6 D.∠A=60°, ∠B=45°,AB=4 6 C D § 3.如图,在△ABC中,∠B=90°,AB=3, BC=4,AC=5,∠1=∠2,则点C到直线 AE的距离是 ( ) § A.3 § B.4 § C.4.5 § D.5 7 B § 4.【2018·贵州黔西南中考】如图,a、b、 c为三角形的边长,则甲、乙、丙三个三角形 和左侧△ABC全等的是 ( ) § A.甲和乙 B.乙和丙 § C.甲和丙 D.只有丙 8 B § 5.【2018·黑龙江牡丹江中考】如图,AC =BC,请你添加一对边或一对角相等的条件, 使AD=BE.你所添加的条件是 ___________________________________ _________________. 9 ∠A=∠B或∠ADC=∠BEC或CE=CD (答案不唯一) § 6.如图,直线a经过正方形ABCD的顶点A, 分别过正方形的顶点B、D作BF⊥a于点F, DE⊥a于点E,若DE=8,BF=5,则EF的 长为______. 10 13 § 7.如图,已知AB=CD,∠B=∠C,AC和 BD相交于点O. § 求证:△AOB≌ △DOC. 11 § 8.【2018·四川宜宾中考】如图,已知∠1 =∠2,∠B=∠D,求证:CB=CD. 12 § 9.如图,已知∠DCE=90°,∠DAC= 90°,BE⊥AC于点B,且DC=EC,若BE =7,AB=3,则AD的长为 ( ) § A.3 § B.5 § C.4 § D.不确定 13 C 14 B § 11.如图,Rt△ABC中,AB⊥AC, AD⊥BC,BE平分∠ABC,交AD于点E, EF∥AC,下列结论一定成立的是 ( ) § A.AB=BF § B.AE=ED § C.AD=DC § D.∠ABE=∠DFE 15 A § 12.如图,在△ABC中,AD⊥BC于点D, BE⊥AC于点E,AD与BE相交于点F,若BF =AC,∠CAD=25°,则∠ABE的度数为 ( ) § A.30° § B.15° § C.25° § D.20° 16 D § 13.如图,△ABC中,∠ACB=90°,AC =BC=5,BE⊥CE于点E,AD⊥CE于点D, AD=4,BE=3,则DE=_____. 17 1 § 14.如图,∠E=∠F=90°,∠B=∠C, AE=AF,给出下列结论:①∠1=∠2; ②CD=DN;③△ACN≌ △ABM;④BE= CF.其中正确的结论有__________. 18 ①③④ § 15.如图,在四边形ABCD中,AB=BC, ∠ABC=∠CDA=90°,BE⊥AD于点E, 且四边形ABCD的面积为12,则BE的长为 _______. 19 § 16.如图,在△ABC中,D是边AB上一点, E是边AC的中点,作CF∥AB交DE的延长线 于点F. § (1)证明:△ADE≌ △CFE; § (2)若AB=AC,CE=5,CF=7,求DB. 20 21 § 17.如图1,在△ABC中,∠ACB=90°, AC=BC,过点C在△ABC外作直线MN, AM⊥MN于点M,BN⊥MN于点N. § (1)求证:MN=AM+BN; § (2)若过点C在△ABC内作直线MN, AM⊥MN于点M,BN⊥MN于点N,则AM、 BN与MN之间有什么关系?请说明理由. 22 23 24查看更多