- 2021-10-26 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
一次函数的应用(1)教案
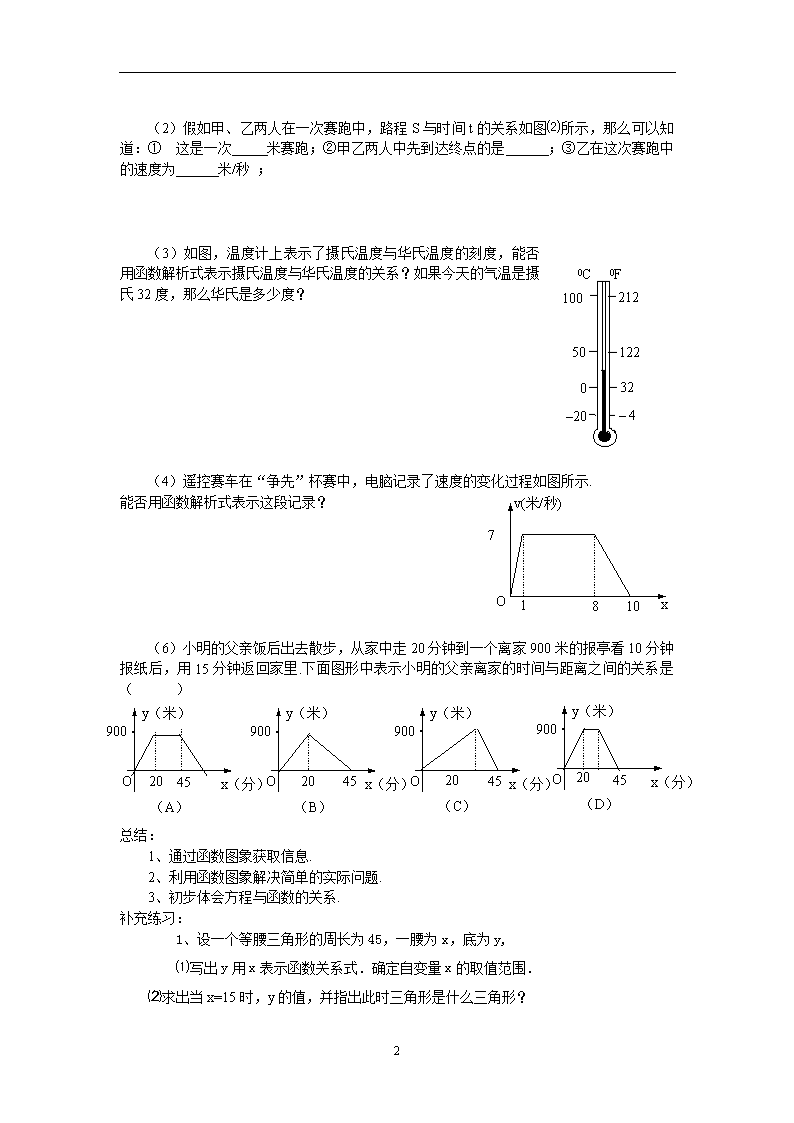
课题:§5.4一次函数的应用(1) 教学目标 1.能根据实际问题中变量之间的关系,确定一次函数关系式. 2.初步体会方程与函数的关系. 3.能通过函数图象获取信息,发展形象思维. 通过函数图象获取信息,培养学生的数形结合意识. 4.根据函数图象解决简单的实际问题,发展学生的教学应用能力. 教学重点 一次函数图象的应用 教学过程 1.新课导入 在前几节课里,我们分别学习了一次函数,一次函数的图象,一次函数图象的特征,并且了解到一次函数的应用十分广泛,和我们日常生活密切相关,因此本节课我们一起来学习一次函数图象的应用. 2.讲授新课 例题1 某校办工厂现年产值是30万元,如果每增加1000元,投资一年可增加2500元产值.那么总产值y(万元)与增加的投资额x(万元)之间的函数关系式为 . 例题2 某市电话的月租费是20元,可打60次免费电话(每次3分钟),超过60次后,超过部分每次0.13元. (1) 写出每月电话费y (元)与通话次数x之间的函数关系式; (2) 分别求出月通话50次、100次的电话费; (3) 如果某月的电话费是27.8元,求该月通话的次数. 例题3 如图中的直线ABC,为甲地向乙地打长途电话所需付的电话费y(元)与通话时间t(分钟)之间的函数关系式的图象.当t ≥2时,该图象的解析式为 ;从图象中可知,通话2分钟需付电话费 元;,通话7分钟需付电话费 元; C B A 3.4 2.4 1.4 O 5 4 3 2 1 ⑴ x y 4.4 · 3、练一练 书P158练习1,2 ⑵ O 12.5 12 100 50 甲 t(秒) S(米) 乙 (1)某种储蓄的月利率是0.8%,存入100元本金后,本息和y(元)与所存月数x之间的函数关系式是 ; 3 (2)假如甲、乙两人在一次赛跑中,路程S与时间t的关系如图⑵所示,那么可以知道:① 这是一次 米赛跑;②甲乙两人中先到达终点的是 ;③乙在这次赛跑中的速度为 米/秒 ; 0F 0C – 4 –20 32 0 50 122 212 100 (3)如图,温度计上表示了摄氏温度与华氏温度的刻度,能否用函数解析式表示摄氏温度与华氏温度的关系?如果今天的气温是摄氏32度,那么华氏是多少度? (4)O 10 8 1 7 v(米/秒) x 遥控赛车在“争先”杯赛中,电脑记录了速度的变化过程如图所示. 能否用函数解析式表示这段记录? · 900 O x(分) y(米) (C) 45 20 · 900 O x(分) y(米) (B) 45 20 · 900 O x(分) y(米) (A) 45 20 · 900 O x(分) y(米) (D) 20 45 (6)小明的父亲饭后出去散步,从家中走20分钟到一个离家900米的报亭看10分钟报纸后,用15分钟返回家里.下面图形中表示小明的父亲离家的时间与距离之间的关系是( ) 总结: 1、通过函数图象获取信息. 2、利用函数图象解决简单的实际问题. 3、初步体会方程与函数的关系. 补充练习: 1、设一个等腰三角形的周长为45,一腰为x,底为y, ⑴写出y用x表示函数关系式.确定自变量x的取值范围. ⑵求出当x=15时,y的值,并指出此时三角形是什么三角形? 3 2、设等腰三角形的顶角为y,底角为x,写出x与y的函数关系式,并确定x的取值范围.若300<x<600,求出y的范围. 3、下表是某个体户卖鱼的斤数与所得钱的关系: 斤数(x) 1 2 3 4 … 所得钱(y) 1.22-0.05 2.44-0.05 3.66-0.05 4.88-0.05 … ⑴从表中可以看出卖7斤鱼得 元钱. ⑵若设所卖鱼的斤数为自变量x,所得钱数为y,请你列出函数关系式,并求出自变量的取值范围. 4、某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)是1吨水的价格(元)的一次函数. ⑴根据下表提供的数据,求y与x的函数关系式.当水价为每吨10元时,10吨水生产出的饮料所获的利润是多少? 1吨水的价格x(元) 4 6 用1吨水生产的饮料所获利润y(元) 200 198 ⑵为节约用水,这个市规定:该厂日用水量不超过20吨时,水价为每吨4元;日用水量超过20吨时,超过部分按每吨20元收费.已知该厂日用水量不少于20吨.设该厂日用水量为t吨,当日所获利润为W元,求W与t的函数关系式. 3查看更多