华师大版八年级数学上册第13章测试题（含答案）

华师大版八年级数学上册第13章测试题（含答案）

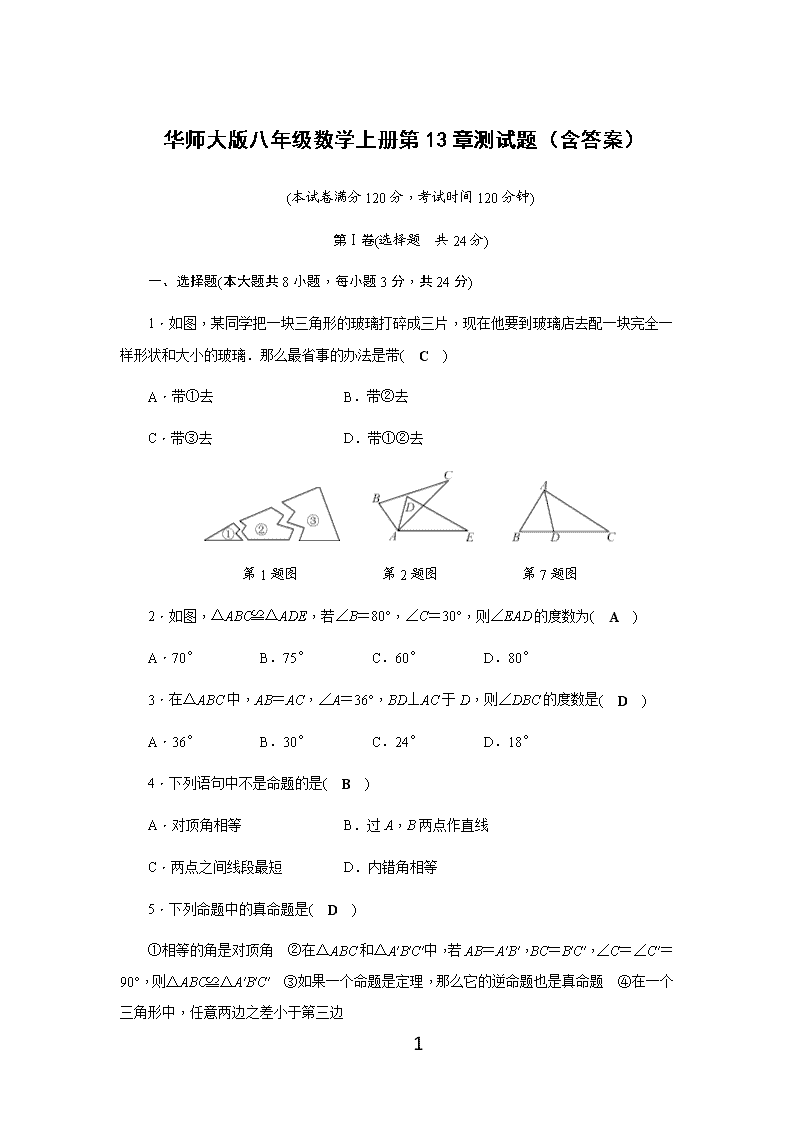
华师大版八年级数学上册第13章测试题（含答案）‎ ‎(本试卷满分120分，考试时间120分钟)‎ 第Ⅰ卷(选择题　共24分)‎ 一、选择题(本大题共8小题，每小题3分，共24分)‎ ‎1．如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状和大小的玻璃．那么最省事的办法是带(　C　)‎ A．带①去　　　　　　　　　 B．带②去 C．带③去 D．带①②去 ‎ ‎ 第1题图 第2题图 第7题图 ‎2．如图，△ABC≌△ADE，若∠B＝80°，∠C＝30°，则∠EAD的度数为(　A　)‎ A．70°　　　　 B．75°　　　　 C．60°　　　　 D．80°‎ ‎3．在△ABC中，AB＝AC，∠A＝36°，BD⊥AC于D，则∠DBC的度数是(　D　)‎ A．36° B．30° C．24° D．18°‎ ‎4．下列语句中不是命题的是(　B　)‎ A．对顶角相等 B．过A，B两点作直线 C．两点之间线段最短 D．内错角相等 ‎5．下列命题中的真命题是(　D　)‎ ‎①相等的角是对顶角　②在△ABC和△A′B′C′中，若AB＝A′B′，BC＝B′C′，∠C＝∠C′＝90°，则△ABC≌△A′B′C′　③如果一个命题是定理，那么它的逆命题也是真命题　④在一个三角形中，任意两边之差小于第三边 8‎ A．①② B．②③ C．③④ D．②④‎ ‎6．下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线，则对应选项中作法错误的是(　C　)‎ A．① B．② C．③ D．④‎ ‎7．如图，在△ABC中，AD为∠BAC的平分线，AB＝2，AC＝3，则△ABD与△ADC的面积之比为(　B　)‎ A．3 ∶2 B．2 ∶3 C．2 ∶5 D．3 ∶5‎ ‎8．★已知等边△ABC的边长为12，D是AB上的动点，过D作DE⊥AC于点E，过E作EF⊥BC于点F，过F作FG⊥AB于点G.当G与D重合时，AD的长是(　C　)‎ A．3 B．4 C．8 D．9‎ 第Ⅱ卷(非选择题　共96分)‎ 二、填空题(本大题共8小题，每小题3分，共24分)‎ ‎9．命题“等腰三角形两腰上的高相等”的逆命题是： 如果一个三角形两边上的高相等，那么这个三角形是等腰三角形 ．‎ ‎10．(上海中考)如图，在△ABC和△DEF中，点B，F，C，E在同一直线上，BF＝CE，AC∥DF，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是 AC＝DF或∠A＝∠D或∠B＝∠E ．(只需写一个，不添加辅助线)‎ 8‎ ‎ ‎ 第10题图　　 第11题图　　 第12题图 ‎11．如图，在△ABC中，∠B＝30°，∠C＝70°，点D是BC上一点，DE⊥AB，DF⊥AC，且DE＝DF，则∠BAD的度数为 40° ．‎ ‎12．★如图，在△ABC中，AB＝AC，分别以点A、点B为圆心，以大于AB的长为半径画弧，两弧相交于点M，N，作直线MN，交AC于点D，连结BD，若△BDC的周长为10，BC＝3，则△ABC的周长为 17 ．‎ ‎13．如果△ABC≌△A′B′C′，AB＝24，S△A′B′C′＝180，那么△ABC中AB边上的高是 15 ．‎ ‎14．如图，已知△ABC是等边三角形，点B，C，D，E在同一直线上，且CG＝CD，DF＝DE，则∠E＝ 15 度．‎ ‎ ‎ 第14题图 　　第16题图 ‎15．★等腰三角形的一腰上的高与另一腰的夹角为45°，则这个三角形的底角为 67.5°或22.5° ．‎ ‎16．如图，∠ABC＝∠DCB，AB＝DC，ME平分∠BMC交BC于点E，结论：①△ABC≌△DCB；②ME垂直平分BC；③△ABM≌△EBM；④△ABM≌△DCM.其中正确的是 ①②④ ．(填序号)‎ 三、解答题(本大题共8小题，共72分)‎ ‎17．(6分)如图：已知点A，E，F，B在一条直线上，AE＝BF，CF＝DE，AC＝BD，求证：GE＝GF.‎ 8‎ 证明：∵AE＝BF，∴AF＋EF＝BE＋EF，即AF＝BE.‎ 在△ACF和△BDE中， ‎∴△ACF≌△BDE(S.S.S.)，∴∠GEF＝∠GFE，∴GE＝GF.‎ ‎18．(6分)已知：如图，点D是△ABC的BC边的中点，DE⊥AC，DF⊥AB，垂足分别为点E，F，且DE＝DF.求证：△ABC是等腰三角形．‎ 证明：∵DE⊥AC，DF⊥AB，‎ ‎∴∠BFD＝∠CED＝90°，‎ ‎∵D是BC的中点，∴BD＝CD，‎ 在Rt△BDF与Rt△CDE中 ‎∴Rt△BDF≌Rt△CDE，‎ ‎∴∠B＝∠C，∴△ABC是等腰三角形．‎ ‎19．(8分)用直尺和圆规作图，求作一条直线把△ABC分成两个三角形，使分后的两个三角形都是等腰三角形．(保留作图痕迹)‎ ‎(1)如图①，△ABC中，∠ABC＝90°，AB＝BC；‎ ‎(2)如图②，△ABC中，∠B＝25°，∠C＝80°.‎ 8‎ 解：(1)如图，过点B作BE⊥AC，垂足为E，作直线BE，则直线BE就是所求作的直线．(方法不唯一)；‎ ‎(2)如图，在∠BAC内作∠BAF＝∠B，交BC于点F，作直线AF，则直线AF就是所求作的直线．‎ ‎20.(10分)如图所示，在△ABC中，∠ACB＝90°，点D是BC延长线上一点，点E是AB上一点，且在BD的垂直平分线EG上，DE交AC于点F.求证：点E在AF的垂直平分线上．‎ 证明：∵EG垂直平分BD，∴EB＝ED，∴∠B＝∠BDE.又∠ACB＝90°，∴∠B＋∠BAC＝90°.又∵∠BDE＋CFD＝90°，∴∠BAC＝∠CFD，又∠CFD＝∠AFE，∴∠BAC＝∠AFE，∴EA＝EF，即E在AF的垂直平分线上．‎ ‎21．(10分)如图：在△ABC，AB＝AC，BD⊥AC于点D，CE⊥AB于点E，BD，CE相交于点F.求证：AF平分∠BAD.‎ 证明：∵BD⊥AC于D，CE⊥AB于E，‎ 8‎ ‎∴∠AEC＝∠ADB＝90°.‎ 在△ABD和△ACE中， ‎∴△ABD≌△ACE(A.A.S.)，∴AE＝AD.‎ 在Rt△AEF和Rt△ADF中， ‎∴Rt△AEF≌Rt△ADF(H.L.)，‎ ‎∴∠EAF＝∠DAF，∴AF平分∠BAD.‎ ‎22.(10分)如图，△ABC中，BD是∠ABC的平分线，CD是外角∠ACE的平分线，连结AD，∠BAC＝70°，求∠CAD的度数．‎ 解：过点D作DM⊥BC于点M，作DN⊥AC于点N，作DP⊥BF于点P.‎ ‎∵BD是∠ABC的平分线，∴DP＝DM，‎ ‎∵CD是∠ACE的平分线，∴DM＝DN，‎ ‎∴DN＝DP.‎ ‎∵DN⊥AC，DP⊥AF，∴AD平分∠CAF.‎ ‎∵∠BAC＝70°，∴∠CAF＝110°，∴∠CAD＝55°.‎ ‎23．(10分)如图，△ABC中，∠1＝∠2，∠C＝2∠B.求证：AB＝AC＋CD.‎ 8‎ 证明：在AB上截取AE＝AC，连结DE，在△ACD和△AED中，‎ ‎∵AE＝AC，∠1＝∠2，AD＝AD，∴△ACD≌△AED(S.A.S.)，∴DE＝DC，∠C＝∠AED.‎ ‎∵∠C＝2∠B，∴∠AED＝2∠B.‎ ‎∵∠AED＝∠B＋∠BDE，∴∠B＝∠BDE，‎ ‎∴BE＝DE(等角对等边)，∴BE＝CD.‎ ‎∵AB＝AE＋BE，∴AB＝AC＋CD.‎ ‎24.(12分)如图，△ABC是等边三角形，点D为BC边上一个动点(点D与B，C均不重合)，AD＝AE，∠DAE＝60°，连结CE.‎ ‎(1)求证：△ABD≌△ACE；‎ ‎(2)求证：CE平分∠ACF；‎ ‎(3)若AB＝2，当四边形ADCE的周长取最小值时，求BD的长．‎ ‎(1)证明：∵△ABC是等边三角形，∴AB＝AC，∠BAC＝60°，‎ ‎∵∠DAE＝60°，∴∠BAD＋∠DAC＝∠CAE＋∠DAC，‎ 即∠BAD＝∠CAE.‎ 在△ABD和△ACE中，∴△ABD≌△ACE；‎ ‎(2)证明：∵△ABC是等边三角形，∴∠B＝∠BCA＝60°，‎ 8‎ ‎∵△ABD≌△ACE，∴∠ACE＝∠B＝60°，∴∠ECF＝180－∠ACE－∠BCA＝60°，‎ ‎∴∠ACE＝∠ECF，∴CE平分∠ACF；‎ ‎(3)解：∵△ABD≌△ACE，∴CE＝BD.‎ ‎∵△ABC是等边三角形，∴AB＝BC＝AC＝2，‎ ‎∴四边形ADCE的周长＝CE＋DC＋AD＋AE＝BD＋DC＋2AD＝2＋2AD，‎ 根据垂线段最短，当AD⊥BC时，AD值最小，四边形ADCE的周长取最小值，‎ ‎∵AB＝AC，∴BD＝BC＝×2＝1.‎ 8‎