2020八年级数学上册 课题：数据的离散程度

2020八年级数学上册 课题：数据的离散程度

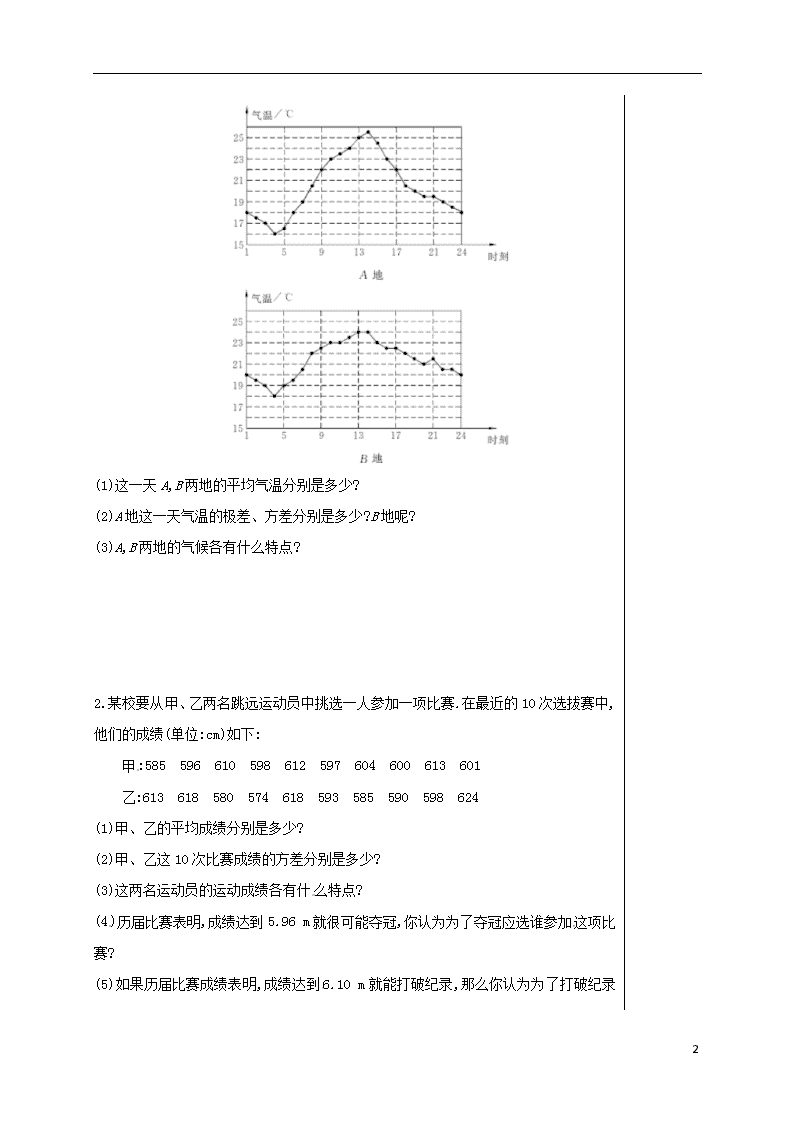
课题：数据的离散程度 班级: 姓名: 小组: 评价: ‎ ‎【学习目标】‎ ‎1、能够用极差、方差统计、分析生活中的简单问题.‎ ‎2、通过实际问题的解释,培养学生解决问题的能力.‎ ‎【重点难点】‎ ‎1. 用方差等概念解释统计过程中反映出的问题.‎ ‎2. 在具体情况下,具体分析方差对问题的影响.‎ ‎【导学流程】‎ 一、基础感知 ‎1.什么叫极差、方差、标准差 ‎2.方差的计算公式是什么?‎ ‎3.已知一组数据5,8,10,x,9的众数是8,那么这组数据的方差是　　　　. ‎ ‎4.人数相等的甲、乙两班学生参加了同一次数学测验,班级平均分和方差如下:平均分都为110,甲、乙两班的方差分别为340,280,则成绩较为稳定的班级为 (　　)‎ A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定 ‎5.已知一组数据:15,13,15,16,17,16,14,15,则这组数据的极差与众数分别是 (　　)‎ A.4,15 B.3,‎15 ‎C.4,16 D.3,16‎ 二、深入学习 利用数据的离散程度来分析问题:‎ ‎1.如图所示的是某一天A,B两地的气温变化图,请回答下列问题:‎ 问题记录 3‎ ‎(1)这一天A,B两地的平均气温分别是多少?‎ ‎(2)A地这一天气温的极差、方差分别是多少?B地呢?‎ ‎(3)A,B两地的气候各有什么特点?‎ ‎2.某校要从甲、乙两名跳远运动员中挑选一人参加一项比赛.在最近的10次选拔赛中,他们的成绩(单位:cm)如下:‎ 甲:585　596　610　598　612　597　604　600　613　601‎ 乙:613　618　580　574　618　593　585　590　598　624‎ ‎(1)甲、乙的平均成绩分别是多少?‎ ‎(2)甲、乙这10次比赛成绩的方差分别是多少?‎ ‎(3)这两名运动员的运动成绩各有什么特点?‎ ‎(4)历届比赛表明,成绩达到‎5.96 m就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?‎ ‎(5)如果历届比赛成绩表明,成绩达到‎6.10 m就能打破纪录,‎ 3‎ 那么你认为为了打破纪录应选谁参加这项比赛?‎ 总结：‎ ‎1.极差的应用多在统计图中考查,要能够准确分析统计图中的量,根据问题进行解答,折线统计图一般能判断数据的稳定性.‎ ‎2.利用方差的大小判断数据稳定性的步骤:‎ ‎①先计算数据的平均数;‎ ‎②计算方差;‎ ‎③根据方差大小作出判断.‎ 三、迁移运用 当堂检测：‎ ‎1.方差是指各个数据与平均数差的平方的　　　　. ‎ ‎2.数据1,6,3,9,8的方差是　　　　. ‎ ‎3.甲、乙两机器分别罐装每瓶质量为‎500‎克的矿泉水,从甲、乙罐装的矿泉水中分别抽取了30瓶,测算它们实际质量的方差是:=4.8,=3.6,那么　　　　罐装的矿泉水质量比较稳定.(填“甲”或“乙”) ‎ ‎4.小明准备参加学校运动会的跳远比赛,下面是他近期六次跳远的成绩(单位:米):3.6,3.8,4.2,4.0,3.8,4.0,那么这组数据的 (　　)‎ ‎　　　　　　　　　　　　　　　‎ A.众数是‎3.9米 B.中位数是‎3.8米 C.极差是‎0.6米 D.平均数是‎4.0米 ‎5.小明和小华本学期都参加了5次数学考试(总分均为100分),数学老师想判断这两位同学谁的数学成绩更稳定,在作统计分析时,老师需比较这两人5次数学成绩的 (　　)‎ A.平均数 B.方差 C.众数 D.中位数 3‎