2019-2020学年安徽宿州八年级上数学期中试卷

2019-2020学年安徽宿州八年级上数学期中试卷

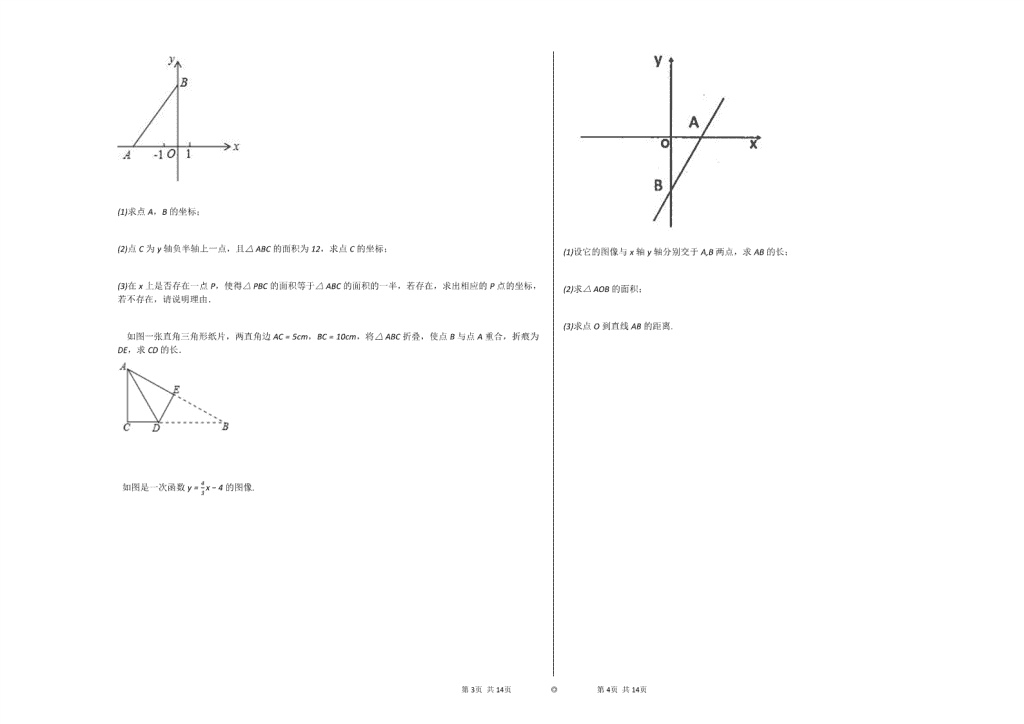
‎2019-2020学年安徽宿州八年级上数学期中试卷 一、选择题 ‎ ‎ ‎1. 下列各组数中，是勾股数的(        ) ‎ A.‎1‎，‎1‎，‎2‎ B.‎1.5‎，‎2‎，‎2.5‎ C.‎7‎，‎24‎，‎25‎ D.‎6‎，‎12‎，‎‎13‎ ‎ ‎ ‎2. 在下列各数‎11‎‎7‎‎、0.37、0.1212212221......、0、π‎2‎、‎25‎、‎3‎‎9‎、0.‎‎3‎‎˙‎‎1‎‎˙‎中无理数的个数是(        )． ‎ A.‎1‎ B.‎2‎ C.‎3‎ D.‎4‎ ‎ ‎ ‎ ‎3. 直角三角形的两条直角边分别为‎5cm，‎12cm，则斜边上的高是(        )cm ‎ A.‎6‎ B.‎8‎ C.‎90‎‎13‎ D.‎‎60‎‎13‎ ‎ ‎ ‎4. ‎9‎的平方根是(        ) ‎ A.‎±3‎ B.‎3‎ C.‎±81‎ D.‎‎±‎‎3‎ ‎ ‎ ‎5. 已知点A(a, 1)‎与点B(5, b)‎关于y轴对称，则实数a，b的值分别是（ ） ‎ A.‎5‎，‎1‎ B.‎−5‎，‎1‎ C.‎5‎，‎−1‎ D.‎−5‎，‎‎−1‎ ‎ ‎ ‎6. 下列函数中是正比例函数的是(        ) ‎ A.y=−‎‎3‎x B.y=−8x C.y=5x‎2‎+6‎ D.‎y=−0.5x−1‎ ‎ ‎ ‎7. 若‎3−m为二次根式，则m的取值为‎(‎        ‎)‎ ‎ A.m≤3‎ B.m<3‎ C.m≥3‎ D.‎m>3‎ ‎ ‎ ‎8. 若点P(m, n)‎在第二象限，则点P(m‎2‎, n)‎在‎(‎        ‎)‎ ‎ A.第一象限 B.第二象限 C.第三象限 D.第四象限 ‎ ‎ ‎9. 点A(x‎1‎, y‎1‎)‎，点B(x‎2‎, y‎2‎)‎是一次函数y=(k‎2‎+1)x+2‎ 的图像上的两点，且x‎1‎‎>‎x‎2‎，则y‎1‎和y‎2‎的大小关系是(         ) ‎ A.y‎1‎‎<‎y‎2‎ B.y‎1‎‎=‎y‎2‎ C.y‎1‎‎>‎y‎2‎ D.不确定 ‎ ‎ ‎10. 已知y=(2m−1)‎xm‎2‎‎−3‎是正比例函数，且y随x的增大而减小，那么这个函数的表达式为(        ) ‎ A.y=−5x B.y=5x C.y=3x D.‎y=−3x 二、填空题 ‎ ‎ ‎ 已知海拔每升高‎1‎千米，温度下降‎6‎​‎‎∘‎C，某时刻A地温度为‎20‎​‎‎∘‎C，高出地面x千米处的温度为y‎​‎‎∘‎C，则y与x之间的函数关系为________． ‎ 三、解答题 ‎ ‎ ‎ 计算 ‎ ‎(1)‎5‎+‎45‎−‎‎1‎‎5‎‎；‎ ‎ ‎ ‎(2)(‎3‎−1‎)‎‎2‎+(‎3‎+2)(‎3‎−2)‎ ‎ ‎ ‎ 求下列各式中的x ‎ ‎(1)‎‎(x+1‎)‎‎2‎−49=0‎‎；‎ ‎ ‎ ‎(2)‎‎8x‎3‎+27=0‎‎．‎ ‎ ‎ ‎ 已知a，b，c，d，e，f是实数，且a，b互为倒数，c，d互为相反数，e是绝对值为‎2‎的数，f的算术平方根是‎8‎，求‎1‎‎2‎ab+c+d‎5‎+e‎2‎+‎‎3‎f的值． ‎ ‎ ‎ ‎ 如图在‎△ABC中，CD⊥AB于点D，AC=20‎，BC=15‎，DB=9‎.求： ‎ ‎1‎CD‎，AD的值；‎ ‎ ‎ ‎2‎‎ 判断‎△ABC的形状，并说明理由．‎ ‎ ‎ 第13页 共14页 ◎ 第14页 共14页 ‎ 如图，在平面直角坐标系中，点A(−3b, 0)‎，为x轴负半轴上一点，点B(0, 4b)‎为y轴正半轴上一点，其中b满足方程‎3(b+1)=6‎. ‎ ‎(1)‎求点A，B的坐标；‎ ‎ ‎ ‎(2)‎点C为y轴负半轴上一点，且‎△ABC的面积为‎12‎，求点C的坐标；‎ ‎ ‎ ‎(3)‎在x上是否存在一点P，使得‎△PBC的面积等于‎△ABC的面积的一半，若存在，求出相应的P点的坐标，若不存在，请说明理由．‎ ‎ ‎ ‎ 如图一张直角三角形纸片，两直角边AC=5cm，BC=10cm，将‎△ABC折叠，使点B与点A重合，折痕为DE，求CD的长． ‎ ‎ ‎ ‎ 如图是一次函数y=‎4‎‎3‎x−4‎的图像. ‎ ‎(1)‎设它的图像与x轴y轴分别交于A,B两点，求AB的长；‎ ‎ ‎ ‎(2)‎求‎△AOB的面积；‎ ‎ ‎ ‎(3)‎求点O到直线AB的距离.‎ 第13页 共14页 ◎ 第14页 共14页 参考答案与试题解析 ‎2019-2020学年安徽宿州八年级上数学期中试卷 一、选择题 ‎1.‎ ‎【答案】‎ C ‎【考点】‎ 勾股数 ‎【解析】‎ 根据勾股数的定义进行分析，从而得到答案．‎ ‎【解答】‎ 解：A，不是，因‎1‎‎2‎‎+‎1‎‎2‎≠‎‎2‎‎2‎； B，不是，因为‎1.5‎，‎2‎，‎2.5‎不是正整数； C，是，因为‎7‎‎2‎‎+‎24‎‎2‎=‎‎25‎‎2‎，且‎7‎、‎24‎、‎25‎是正整数； D，不是，因为‎6‎‎2‎‎+‎12‎‎2‎≠‎‎13‎‎2‎． 故选C．‎ ‎2.‎ ‎【答案】‎ C ‎【考点】‎ 无理数的判定 ‎【解析】‎ 根据无理数的定义解答．‎ ‎【解答】‎ 解：‎0.1212212221......、π‎2‎、‎‎3‎‎9‎是无限不循环小数，为无理数，有‎3‎个. 故选C．‎ ‎3.‎ ‎【答案】‎ D ‎【考点】‎ 三角形的面积 勾股定理 ‎【解析】‎ 先根据勾股定理可求出斜边．然后由于同一三角形面积一定，可列方程直接解答．‎ ‎【解答】‎ 解：∵ 直角三角形的两条直角边分别为‎5cm，‎12cm， ∴ 斜边‎=‎5‎‎2‎‎+‎‎12‎‎2‎=13cm， 设斜边上的高为h，则直角三角形的面积‎=‎1‎‎2‎×5×12=‎1‎‎2‎×13⋅h， ∴ h=‎60‎‎13‎cm． 故选D．‎ ‎4.‎ ‎【答案】‎ D ‎【考点】‎ 算术平方根 平方根 ‎【解析】‎ 求出‎81‎‎=9‎，求出‎9‎的平方根即可．‎ ‎【解答】‎ 解：∵ ‎9‎‎=3‎， ∴ ‎9‎的平方根是‎±‎‎3‎. 故选D.‎ ‎5.‎ ‎【答案】‎ B ‎【考点】‎ 关于x轴、y轴对称的点的坐标 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：∵ 点A(a, 1)‎与点B(5, b)‎关于y轴对称， ∴ a=−5‎，b=1‎， 故选B．‎ ‎6.‎ ‎【答案】‎ B ‎【考点】‎ 正比例函数的定义 一次函数的定义 二次函数的定义 反比例函数的定义 ‎【解析】‎ 根据正比例函数的定义：一般地，形如y=kx(k是常数，k≠0)‎的函数叫做正比例函数，其中k叫做比例系数可得答案．‎ ‎【解答】‎ 解：A，y是x的反比例函数，故此选项错误； B，y是x的正比例函数，故此选项正确； C，是二次函数，故此选项错误； D，y是x的一次函数，故此选项错误. 故选B．‎ ‎7.‎ ‎【答案】‎ A 第13页 共14页 ◎ 第14页 共14页 ‎【考点】‎ 二次根式有意义的条件 ‎【解析】‎ 根据二次根式中的被开方数必须是非负数列出不等式，解不等式即可．‎ ‎【解答】‎ 解：由题意得，‎3−m≥0‎， 解得：m≤3‎， 故选A．‎ ‎8.‎ ‎【答案】‎ A ‎【考点】‎ 点的坐标 ‎【解析】‎ 根据第二象限内点的横坐标是负数，纵坐标是正数判断出m、n的正负情况，再根据各象限内点的坐标特征判断点N所在的象限即可．‎ ‎【解答】‎ 解：∵ 点P(m, n)‎在第二象限， ∴ m<0‎，n>0‎， ∴ m‎2‎‎>0‎， ∴ P(m‎2‎, n)‎在第一象限． 故选A．‎ ‎9.‎ ‎【答案】‎ C ‎【考点】‎ 一次函数的性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：∵ 一次函数y=(k‎2‎+1)x+2‎， ∴ 此函数中y随x的增大而增大， ∵ x‎1‎‎>‎x‎2‎， ∴ y‎1‎‎>‎y‎2‎． 故选C．‎ ‎10.‎ ‎【答案】‎ A ‎【考点】‎ 正比例函数的性质 正比例函数的定义 ‎【解析】‎ 形如y=kx(k是常数，k≠0)‎的函数叫做正比例函数，‎ ‎【解答】‎ 解：∵ y=(2m−1)‎xm‎2‎‎−3‎是正比例函数，且y随x的增大而减小， ∴ ‎2m−1<0‎m‎2‎‎−3=1‎， 解得：m<‎‎1‎‎2‎，m=±2‎， ∴ m=−2‎． ∴ 这个函数的表达式为y=−5x. 故选A．‎ 二、填空题 ‎【答案】‎ y=20−6x ‎【考点】‎ 函数关系式 ‎【解析】‎ 根据气温‎=‎山脚的气温-下降的气温列出函数解析式．‎ ‎【解答】‎ 解：依题意有：y=20−6x． 故y和x的函数关系式是y=20−6x． 故答案是：y=20−6x．‎ 三、解答题 ‎【答案】‎ 解：‎(1)‎原式‎=‎5‎+3‎5‎−‎‎5‎‎5‎ ‎=‎‎19‎‎5‎‎5‎.‎ ‎(2)‎原式‎=(‎3‎‎)‎‎2‎−2‎3‎+1+(‎3‎‎)‎‎2‎−‎‎2‎‎2‎ ‎=3−2‎3‎+1+3−4‎ ‎=3−2‎‎3‎.‎ ‎【考点】‎ 二次根式的性质与化简 平方差公式 完全平方公式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎原式‎=‎5‎+3‎5‎−‎‎5‎‎5‎ ‎=‎‎19‎‎5‎‎5‎.‎ ‎(2)‎原式‎=(‎3‎‎)‎‎2‎−2‎3‎+1+(‎3‎‎)‎‎2‎−‎‎2‎‎2‎ ‎=3−2‎3‎+1+3−4‎ ‎=3−2‎‎3‎.‎ ‎【答案】‎ 解：‎(1)‎‎(x+1‎)‎‎2‎−49=0‎， ‎(x+1‎)‎‎2‎=49‎， x+1=±7‎， 解得：‎x‎1‎‎=6，x‎2‎=−8‎ 第13页 共14页 ◎ 第14页 共14页 ‎.‎ ‎(2)‎‎8x‎3‎+27=0‎‎， ‎8x‎3‎=−27‎， x‎3‎‎=‎‎−27‎‎8‎， 解得：x=−‎‎3‎‎2‎.‎ ‎【考点】‎ 立方根的性质 平方根 ‎【解析】‎ ‎（1）根据开平方解答即可；‎ ‎（2）根据开立方解答即可．‎ ‎【解答】‎ 解：‎(1)‎‎(x+1‎)‎‎2‎−49=0‎， ‎(x+1‎)‎‎2‎=49‎， x+1=±7‎， 解得：x‎1‎‎=6，x‎2‎=−8‎.‎ ‎(2)‎‎8x‎3‎+27=0‎‎， ‎8x‎3‎=−27‎， x‎3‎‎=‎‎−27‎‎8‎， 解得：x=−‎‎3‎‎2‎.‎ ‎【答案】‎ 解：由题意可知：ab=1‎，c+d=0‎，e=±‎‎2‎，f=64‎， ∴ e‎2‎‎=(±‎2‎‎)‎‎2‎=2‎，‎3‎f‎=‎3‎‎64‎=4‎， ∴ ‎1‎‎2‎ab+c+d‎5‎+e‎2‎+‎3‎f=‎1‎‎2‎+0+2+4=6‎‎1‎‎2‎．‎ ‎【考点】‎ 实数的运算 算术平方根 倒数 绝对值 相反数 ‎【解析】‎ 根据相反数，倒数，以及绝对值的意义求出c+d，ab及e的值，代入计算即可．‎ ‎【解答】‎ 解：由题意可知：ab=1‎，c+d=0‎，e=±‎‎2‎，f=64‎， ∴ e‎2‎‎=(±‎2‎‎)‎‎2‎=2‎，‎3‎f‎=‎3‎‎64‎=4‎， ∴ ‎1‎‎2‎ab+c+d‎5‎+e‎2‎+‎3‎f=‎1‎‎2‎+0+2+4=6‎‎1‎‎2‎．‎ ‎【答案】‎ 解：‎1‎∵ 在Rt△BCD中，BC=15‎，BD=9‎， ∴ CD=BC‎2‎−BD‎2‎=‎15‎‎2‎‎−‎‎9‎‎2‎=12‎． 在Rt△ADC中，AC=20‎，CD=12‎， ∴ AD=AC‎2‎−CD‎2‎=‎20‎‎2‎‎−‎‎12‎‎2‎=16‎．‎ ‎2‎‎△ABC是直角三角形. 理由：∵ AB=25‎，AC=20‎，BC=15‎， ∴ AB‎2‎=‎25‎‎2‎=625‎， AC‎2‎+BC‎2‎=‎20‎‎2‎+‎15‎‎2‎=625‎， ∴ AB‎2‎=AC‎2‎+BC‎2‎， ∴ ‎△ABC是直角三角形．‎ ‎【考点】‎ 勾股定理的逆定理 勾股定理 ‎【解析】‎ ‎（1）在Rt△BCD中利用勾股定理求得CD的长，然后在Rt△ADC中求得AD的长，根据AB=AD+DB即可求解；‎ ‎（2）利用勾股定理的逆定理即可判断．‎ ‎【解答】‎ 解：‎1‎∵ 在Rt△BCD中，BC=15‎，BD=9‎， ∴ CD=BC‎2‎−BD‎2‎=‎15‎‎2‎‎−‎‎9‎‎2‎=12‎． 在Rt△ADC中，AC=20‎，CD=12‎， ∴ AD=AC‎2‎−CD‎2‎=‎20‎‎2‎‎−‎‎12‎‎2‎=16‎．‎ ‎2‎‎△ABC是直角三角形. 理由：∵ AB=25‎，AC=20‎，BC=15‎， ∴ AB‎2‎=‎25‎‎2‎=625‎， AC‎2‎+BC‎2‎=‎20‎‎2‎+‎15‎‎2‎=625‎， ∴ AB‎2‎=AC‎2‎+BC‎2‎， ∴ ‎△ABC是直角三角形．‎ ‎【答案】‎ 解：‎(1)‎解方程：‎3(b+1)=6‎，得：b=1‎， ∴ A(−3, 0)‎，B(0, 4)‎.‎ ‎(2)‎‎∵ A(−3, 0)‎， ∴ OA=3‎， ∵ ‎△ABC的面积为‎12‎，S‎△ABC‎=‎1‎‎2‎BC⋅OA=‎1‎‎2‎×BC×3=12‎， ∴ BC=8‎， ∵ B(0, 4)‎， ∴ OB=4‎， ∵ 点C为y轴负半轴上一点， ∴ OC=4‎， ∴ C(0, −4)‎.‎ ‎(3)‎存在. ∵ ‎△PBC的面积等于‎△ABC的面积的一半， ∴ BC上的高OP为‎3‎‎2‎， ∴ 点P的坐标‎(‎3‎‎2‎, 0)‎ 第13页 共14页 ◎ 第14页 共14页 或‎(−‎3‎‎2‎, 0)‎．‎ ‎【考点】‎ 三角形的面积 坐标与图形性质 点的坐标 ‎【解析】‎ ‎（1）得出b的值后代入解答即可；‎ ‎（2）根据三角形的面积公式得出点C的坐标即可；‎ ‎（3）根据‎△PBC的面积等于‎△ABC的面积的一半得出OP解答即可．‎ ‎【解答】‎ 解：‎(1)‎解方程：‎3(b+1)=6‎，得：b=1‎， ∴ A(−3, 0)‎，B(0, 4)‎.‎ ‎(2)‎‎∵ A(−3, 0)‎， ∴ OA=3‎， ∵ ‎△ABC的面积为‎12‎，S‎△ABC‎=‎1‎‎2‎BC⋅OA=‎1‎‎2‎×BC×3=12‎， ∴ BC=8‎， ∵ B(0, 4)‎， ∴ OB=4‎， ∵ 点C为y轴负半轴上一点， ∴ OC=4‎， ∴ C(0, −4)‎.‎ ‎(3)‎存在. ∵ ‎△PBC的面积等于‎△ABC的面积的一半， ∴ BC上的高OP为‎3‎‎2‎， ∴ 点P的坐标‎(‎3‎‎2‎, 0)‎或‎(−‎3‎‎2‎, 0)‎．‎ ‎【答案】‎ 解：由折叠知：DA=DB，‎△ACD为直角三角形． 在Rt△ACD中，AC‎2‎+CD‎2‎=AD‎2‎①， 设CD=x cm，则AD=BD=(10−x)cm， 代入①式得‎5‎‎2‎‎+x‎2‎=(10−x‎)‎‎2‎， 化简得‎25=100−20x， 所以x=‎15‎‎4‎cm ， 即CD的长为‎15‎‎4‎cm．‎ ‎【考点】‎ 勾股定理 翻折变换（折叠问题）‎ ‎【解析】‎ 由翻折易得DB=AD，利用直角三角形ACD，勾股定理即可求得CD长．‎ ‎【解答】‎ 解：由折叠知：DA=DB，‎△ACD为直角三角形． 在Rt△ACD中，AC‎2‎+CD‎2‎=AD‎2‎①， 设CD=x cm，则AD=BD=(10−x)cm， 代入①式得‎5‎‎2‎‎+x‎2‎=(10−x‎)‎‎2‎， 化简得‎25=100−20x， 所以x=‎15‎‎4‎cm ， 即CD的长为‎15‎‎4‎cm．‎ ‎【答案】‎ 解：‎(1)‎令y=0‎，则x=3‎, 则A点坐标为‎(3,0)‎,OA长‎=3‎； 令x=0‎，则y=−4‎, 则B点坐标为‎(−4,0)‎,OB长‎=4‎. 则AB长为OA‎2‎+OB‎2‎‎=5‎.‎ ‎(2)‎由‎(1)‎得OA=3,0B=4‎， 则‎△AOB的面积‎=‎1‎‎2‎×OA×OB=‎1‎‎2‎×3×4=6‎.‎ ‎(3)‎由‎(1)‎得AB=5‎, 由‎(2)‎得‎△AOB的面积为‎6‎, 设O到直线距离为x， 则有‎1‎‎2‎‎×AB×x=6‎， 解得x=‎‎12‎‎5‎. 则点O到直线AB的距离为‎12‎‎5‎.‎ ‎【考点】‎ 一次函数图象上点的坐标特点 三角形的面积 勾股定理 点到直线的距离 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎令y=0‎，则x=3‎, 则A点坐标为‎(3,0)‎,OA长‎=3‎； 令x=0‎，则y=−4‎, 则B点坐标为‎(−4,0)‎,OB长‎=4‎. 则AB长为OA‎2‎+OB‎2‎‎=5‎.‎ ‎(2)‎由‎(1)‎得OA=3,0B=4‎， 则‎△AOB的面积‎=‎1‎‎2‎×OA×OB=‎1‎‎2‎×3×4=6‎.‎ 第13页 共14页 ◎ 第14页 共14页 ‎(3)‎由‎(1)‎得AB=5‎, 由‎(2)‎得‎△AOB的面积为‎6‎, 设O到直线距离为x， 则有‎1‎‎2‎‎×AB×x=6‎， 解得x=‎‎12‎‎5‎. 则点O到直线AB的距离为‎12‎‎5‎.‎ 第13页 共14页 ◎ 第14页 共14页