八年级下册数学教案20-1-2 第1课时 中位数和众数 人教版

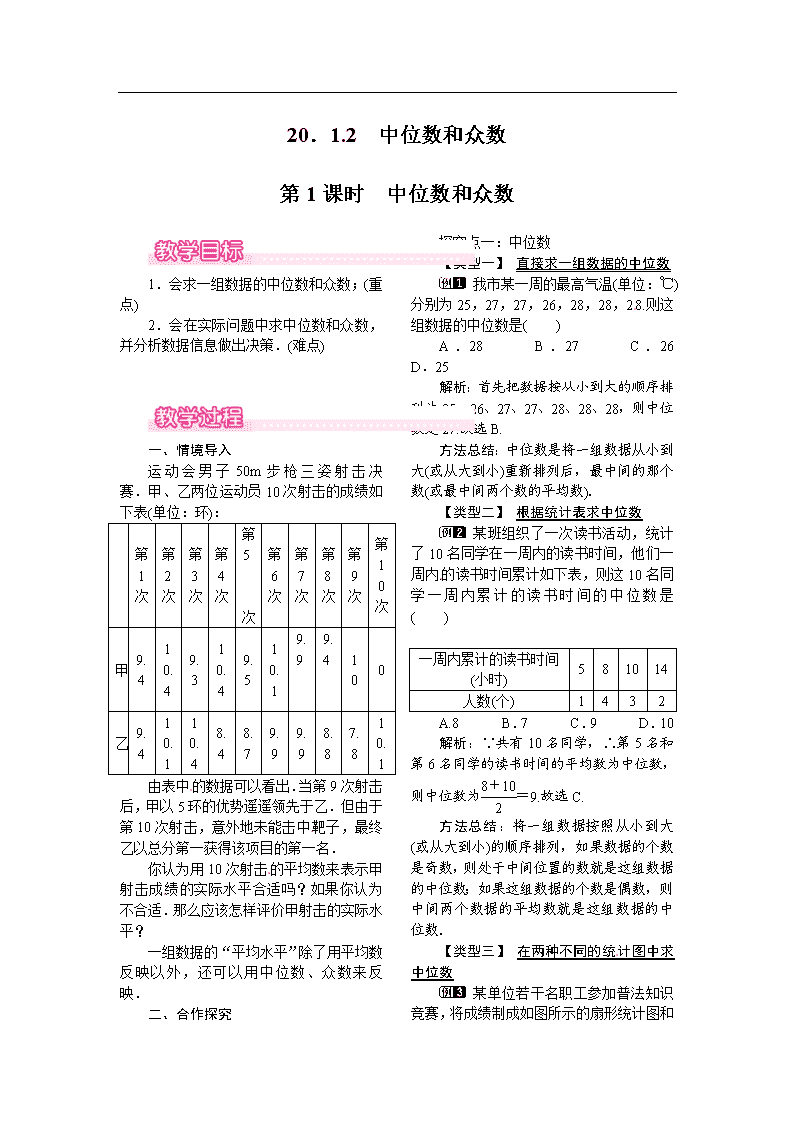
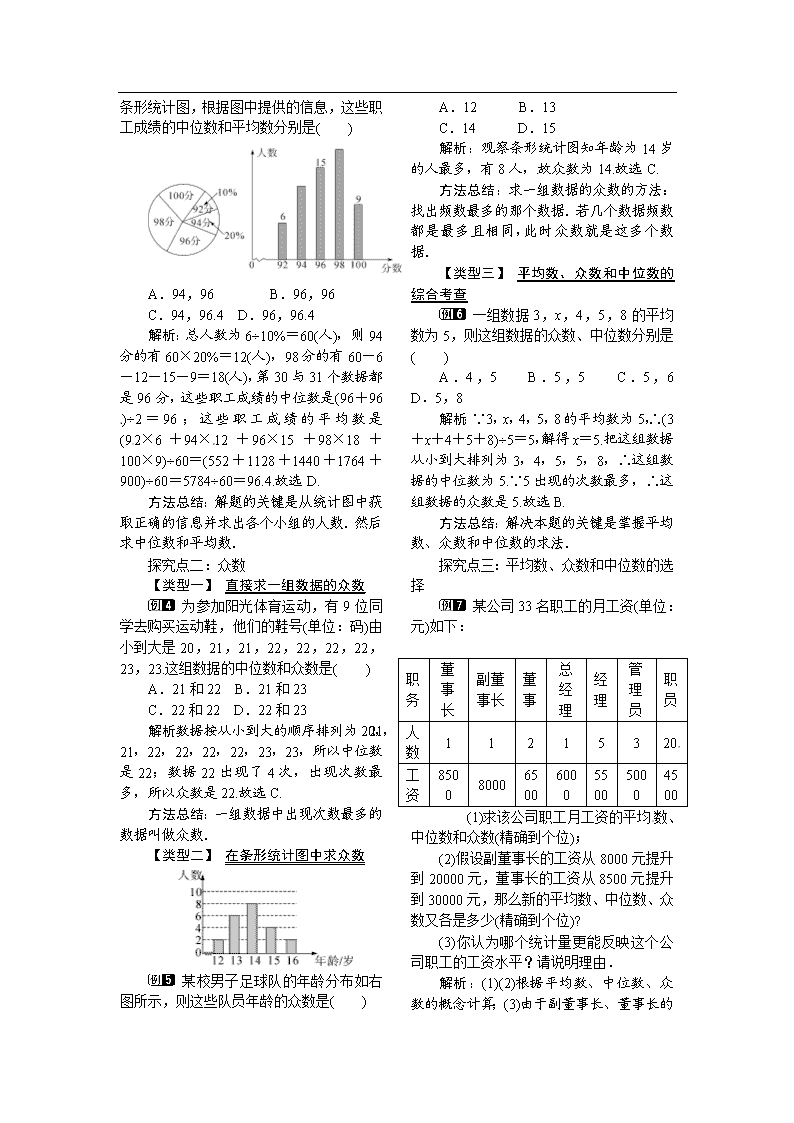
八年级下册数学教案20-1-2 第1课时 中位数和众数 人教版

‎20．1.2　中位数和众数 第1课时　中位数和众数 ‎1．会求一组数据的中位数和众数；(重点)‎ ‎2．会在实际问题中求中位数和众数，并分析数据信息做出决策．(难点)‎ ‎　　　　　　　　　　　　　　　　　　‎ 一、情境导入 运动会男子50m步枪三姿射击决赛．甲、乙两位运动员10次射击的成绩如下表(单位：环)：‎ 第 ‎1‎ 次 第 ‎2‎ 次 第 ‎3‎ 次 第 ‎4‎ 次 第 ‎5[来源:Z*xx*k.Com]‎ 次 第 ‎6‎ 次 第 ‎7‎ 次 第 ‎8‎ 次 第 ‎9‎ 次 第 ‎10‎ 次 甲 ‎9.4‎ ‎10.4‎ ‎9.3‎ ‎10.4‎ ‎9.5‎ ‎10.1‎ ‎9.9[来源:学科网ZXXK]‎ ‎9.4[来源:学科网ZXXK]‎ ‎10‎ ‎0‎ 乙 ‎9.4‎ ‎10.1‎ ‎10.4‎ ‎8.4‎ ‎8.7‎ ‎9.9‎ ‎9.9‎ ‎8.8‎ ‎7.8‎ ‎10.1‎ 由表中的数据可以看出．当第9次射击后，甲以5环的优势遥遥领先于乙．但由于第10次射击，意外地未能击中靶子，最终乙以总分第一获得该项目的第一名．‎ 你认为用10次射击的平均数来表示甲射击成绩的实际水平合适吗？如果你认为不合适．那么应该怎样评价甲射击的实际水平？‎ 一组数据的“平均水平”除了用平均数反映以外，还可以用中位数、众数来反映．‎ 二、合作探究 探究点一：中位数 ‎【类型一】 直接求一组数据的中位数 ‎ 我市某一周的最高气温(单位：℃)分别为25，27，27，26，28，28，28.则这组数据的中位数是(　　)‎ A．28　　　B．27　　　C．26　　　D．25‎ 解析：首先把数据按从小到大的顺序排列为25、26、27、27、28、28、28，则中位数是27.故选B.‎ 方法总结：中位数是将一组数据从小到大(或从大到小)重新排列后，最中间的那个数(或最中间两个数的平均数)．‎ ‎【类型二】 根据统计表求中位数 ‎ 某班组织了一次读书活动，统计了10名同学在一周内的读书时间，他们一周内的读书时间累计如下表，则这10名同学一周内累计的读书时间的中位数是(　　)[来源:学科网ZXXK]‎ 一周内累计的读书时间(小时)‎ ‎5‎ ‎8‎ ‎10‎ ‎14‎ 人数(个)‎ ‎1‎ ‎4‎ ‎3‎ ‎2‎ A.8　　　B．7　　　C．9　　　D．10‎ 解析：∵共有10名同学，∴第5名和第6名同学的读书时间的平均数为中位数，则中位数为＝9.故选C.‎ 方法总结：将一组数据按照从小到大(或从大到小)的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．‎ ‎【类型三】 在两种不同的统计图中求中位数 ‎ 某单位若干名职工参加普法知识竞赛，将成绩制成如图所示的扇形统计图和条形统计图，根据图中提供的信息，这些职工成绩的中位数和平均数分别是(　　)‎ A．94，96　　　　B．96，96‎ C．94，96.4 D．96，96.4[来源:学#科#网Z#X#X#K]‎ 解析：总人数为6÷10%＝60(人)，则94分的有60×20%＝12(人)，98分的有60－6－12－15－9＝18(人)，第30与31个数据都是96分，这些职工成绩的中位数是(96＋96)÷2＝96；这些职工成绩的平均数是(92×6＋94×12＋96×15＋98×18＋100×9)÷60＝(552＋1128＋1440＋1764＋900)÷60＝5784÷60＝96.4.故选D.‎ 方法总结：解题的关键是从统计图中获取正确的信息并求出各个小组的人数．然后求中位数和平均数．‎ 探究点二：众数 ‎【类型一】 直接求一组数据的众数 ‎ 为参加阳光体育运动，有9位同学去购买运动鞋，他们的鞋号(单位：码)由小到大是20，21，21，22，22，22，22，23，23.这组数据的中位数和众数是(　　)‎ A．21和22 B．21和23‎ C．22和22 D．22和23‎ 解析：数据按从小到大的顺序排列为20，21，21，22，22，22，22，23，23，所以中位数是22；数据22出现了4次，出现次数最多，所以众数是22.故选C.‎ 方法总结：一组数据中出现次数最多的数据叫做众数．‎ ‎【类型二】 在条形统计图中求众数 ‎ 某校男子足球队的年龄分布如右图所示，则这些队员年龄的众数是(　　)‎ A．12　　　B．13‎ C．14　　　D．15‎ 解析：观察条形统计图知年龄为14岁的人最多，有8人，故众数为14.故选C.‎ 方法总结：求一组数据的众数的方法：找出频数最多的那个数据．若几个数据频数都是最多且相同，此时众数就是这多个数据．‎ ‎【类型三】 平均数、众数和中位数的综合考查 ‎ 一组数据3，x，4，5，8的平均数为5，则这组数据的众数、中位数分别是(　　)‎ A．4，5　　B．5，5　　C．5，6　　D．5，8‎ 解析：∵3，x，4，5，8的平均数为5，∴(3＋x＋4＋5＋8)÷5＝5，解得x＝5.把这组数据从小到大排列为3，4，5，5，8，∴这组数据的中位数为5.∵5出现的次数最多，∴这组数据的众数是5.故选B.‎ 方法总结：解决本题的关键是掌握平均数、众数和中位数的求法．‎ 探究点三：平均数、众数和中位数的选择 ‎ 某公司33名职工的月工资(单位：元)如下：‎ 职务 董事长 副董事长 董事 总经理 经理 管理员 职员 人数 ‎1‎ ‎1‎ ‎2‎ ‎1‎ ‎5‎ ‎3‎ ‎20‎ 工资 ‎8500‎ ‎8000‎ ‎6500‎ ‎6000‎ ‎5500‎ ‎5000‎ ‎4500‎ ‎　　(1)求该公司职工月工资的平均数、中位数和众数(精确到个位)；‎ ‎(2)假设副董事长的工资从8000元提升到20000元，董事长的工资从8500元提升到30000元，那么新的平均数、中位数、众数又各是多少(精确到个位)?‎ ‎(3)你认为哪个统计量更能反映这个公司职工的工资水平？请说明理由．‎ 解析：‎ ‎(1)(2)根据平均数、中位数、众数的概念计算；(3)由于副董事长、董事长的工资偏高，使月平均工资偏大，也就是说用平均数来反映这个公司职工的工资水平有很大的误差．应用公司职工月工资的中位数或众数来反映这个公司的工资水平．‎ 解：(1)公司职工月工资的平均数为×(8500＋8000＋6500×2＋6000＋5500×5＋5000×3＋4500×20)≈5091；把33个数据按从小到大排列可得中位数为4500，众数为4500；‎ ‎(2)新的平均数为×(30000＋20000＋6500×2＋6000＋5500×5＋5000×3＋4500×20)≈6106；把33个新的数据按从小到大排列可得中位数仍为4500，众数仍为4500；‎ ‎(3)由于副董事长、董事长的工资偏高，使月平均工资与绝大多数职工的月工资差距很大，也就是说用平均数来反映这个公司职工的工资水平有很大的误差．显然用公司职工月工资的中位数或众数更能反映这个公司的工资水平．‎ 方法总结：此题主要考查统计的有关知识，主要包括平均数、中位数、众数的意义．反映数据集中程度的平均数、中位数、众数各有局限性，因此要对统计量进行合理的选择和恰当的运用．‎ 三、板书设计 ‎1．中位数 ‎2．众数 ‎3．平均数、众数和中位数的应用 通过学生观察、分析、讨论，在共享集体思维成果的基础上逐步建构出中位数及众数的概念，这样做使学生逐步体会到这两个统计量都反映一组数据的集中趋势，但是描述的角度并不同，这样可以比较全面、‎ 正确地理解所学知识．在教学中，对学生的各种回答给予肯定，各人从不同的角度理解会得到不同的结论．然后通过学生合作交流，相互完善，在自主探索中发现概念的形成过程．让学生认识到研究数据的必要性．‎