人教版八年级数学下册第十七章《勾股定理》单元同步检测试题（含答案）

人教版八年级数学下册第十七章《勾股定理》单元同步检测试题（含答案）

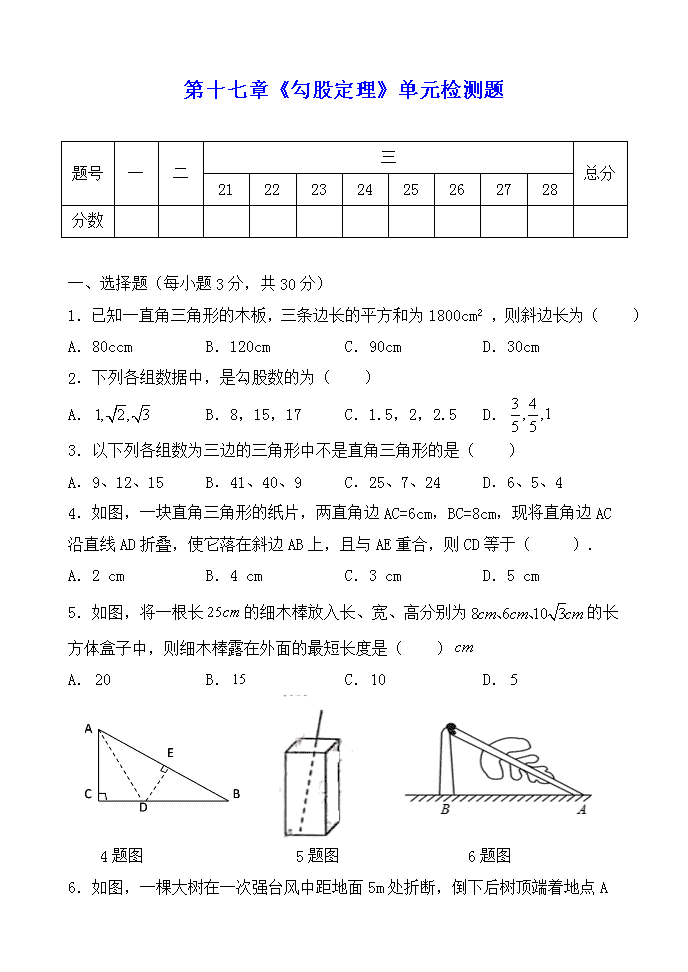
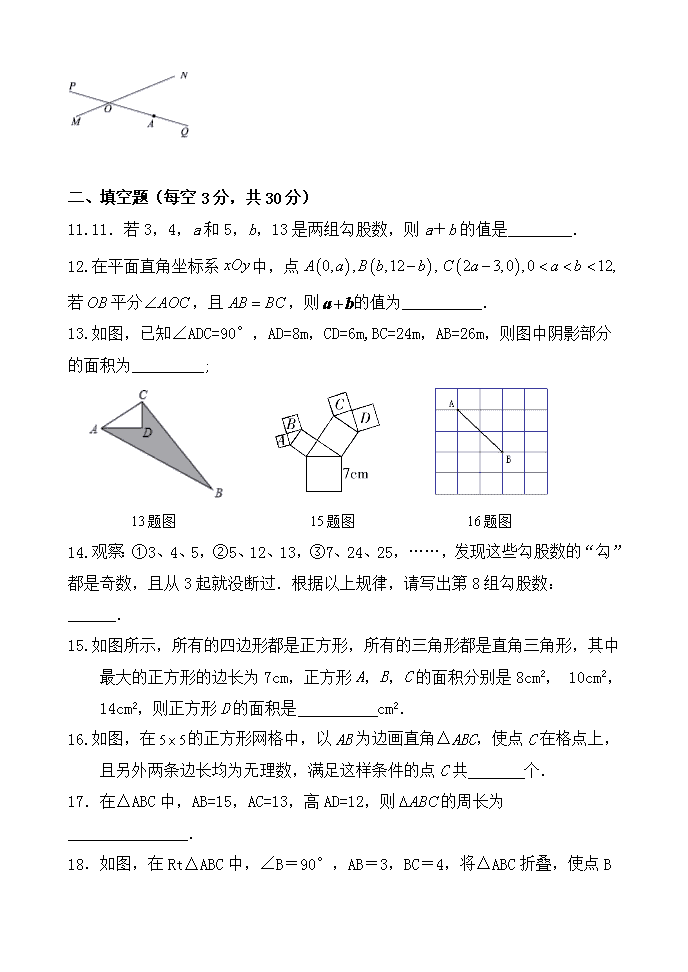
第十七章《勾股定理》单元检测题题号一二三总分2122232425262728分数一、选择题（每小题3分，共30分）1．已知一直角三角形的木板，三条边长的平方和为1800cm2，则斜边长为（）A．80ccmB．120cmC．90cmD．30cm2．下列各组数据中，是勾股数的为（）A．B．8，15，17C．1.5，2，2.5D．3．以下列各组数为三边的三角形中不是直角三角形的是（）A．9、12、15B．41、40、9C．25、7、24D．6、5、44．如图，一块直角三角形的纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（　　）.A．2cmB．4cmC．3cmD．5cm5．如图，将一根长的细木棒放入长、宽、高分别为的长方体盒子中，则细木棒露在外面的最短长度是（）A．B．C．D．4题图5题图6题图6．如图，一棵大树在一次强台风中距地面5m处折断，倒下后树顶端着地点A 距树底端B的距离为12m，这棵大树在折断前的高度为（）A．10mB．15mC．18mD．20m7．若△ABC的三边长分别为a、b、c且满足（a+b）（a2+b2﹣c2）＝0，则△ABC是（　　）A．等腰三角形B．直角三角形C．等腰三角形或直角三角形D．等腰直角三角形8．如图为某楼梯，测得楼梯的长为5米，高为3米，计划在楼梯表面铺地毯，则地毯的长度至少需要(　　)A．5米B．7米C．8米D．12米9．如图是一块长、宽、高分别是6cm，4cm，3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需爬行的最短路程是(　　)A．(3＋2)cmB．cmC．cmD．cm10．如图，铁路MN和公路PQ在点O处交会，∠QON＝30°.公路PQ上A处距离O点240m．如果火车行驶时，周围200m以内会受到噪音的影响，那么火车在铁路MN上沿ON方向以72km/h的速度行驶时，A处受噪音影响的时间为(　　)A．12sB.16sC．20sD.24s 二、填空题（每空3分，共30分）11.11．若3，4，a和5，b，13是两组勾股数，则a＋b的值是________．12.在平面直角坐标系中，点若平分，且，则的值为__________．13.如图，已知∠ADC=90°，AD=8m，CD=6m,BC=24m，AB=26m，则图中阴影部分的面积为_________;13题图15题图16题图14.观察：①3、4、5，②5、12、13，③7、24、25，……，发现这些勾股数的“勾”都是奇数，且从3起就没断过．根据以上规律，请写出第8组勾股数：______．15.如图所示，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，正方形A，B，C的面积分别是8cm2，10cm2，14cm2，则正方形D的面积是cm2．16.如图，在的正方形网格中，以AB为边画直角△ABC，使点C在格点上，且另外两条边长均为无理数，满足这样条件的点C共个．17．在△ABC中，AB=15，AC=13，高AD=12，则的周长为_______________．18．如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B 恰好落在边AC上，与点B′重合，AE为折痕，则EB′＝_______．19．如图，正方形的边长均为1，可以计算出，图（1）中正方形的对角线长为；图（2）中长方形的对角线长为；图（3）中长方形对角线的长为，那么第n个长方形的对角线的长为_____．20．有一块田地的形状和尺寸如图，则它的面积为_________.三、解答题（满分60分）．21.(5分)在数轴上作出表示及的点．22．(6分)如图，在中，∠C＝90°，、、分别表示、、的对边．BACabc（1）已知c＝25，a:b＝4:3，求a、b；（2）已知a＝，∠A＝60°，求b、c．23．(6分)如图，在△ABC中，CD⊥AB于D，AB ＝AC＝13，BD＝1.求：(1)CD的长；(2)BC的长．24．7分)如图，已知CD＝6，AB＝4，∠ABC＝∠D＝90°，BD＝DC，求AC的长．25．(8分)如图，在四边形ABCD中，AB＝AD＝2，BC＝3，CD＝1，∠A＝90°，求∠ADC的度数．26．(8分)如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.27．(10分)如图，已知某学校A与直线公路BD的距离AB为3000米，且与该公路上的一个车站D相距5000米，现要在公路边建一个超市C，使之与学校A及车站D的距离相等，那么该超市与车站D的距离是多少米？ 28．(10分)若△ABC的三边长a，b，c满足a2＋b2＋c2＋50＝6a＋8b＋10c，判断△ABC的形状．《勾股定理》章节测试题答案一．选择题1．D2．B．3．D4．C．5．A．6．B．7.D8.B9.C10.B二．填空题11．1712．13．96m2．14．17，144，14515.1716．4．17．32或4218．1.519．．20．96． 三．解答题．21．略．（表示对每个数2分）22．（1）a=20，b=15．（2），．（每小题4分）23.解：(1)∵AB＝13，BD＝1，∴AD＝13－1＝12.在Rt△ACD中，CD＝＝＝5.(2)在Rt△BCD中，BC＝＝＝.24.解：在Rt△BDC，Rt△ABC中，BC2＝BD2＋DC2，AC2＝AB2＋BC2，则AC2＝AB2＋BD2＋DC2，又因为BD＝DC，则AC2＝AB2＋2CD2＝42＋2×62＝88，∴AC＝2，即AC的长为225．解：连接BD.在Rt△BAD中，因为AB＝AD＝2，所以∠ADB＝45°，BD2＝AD2＋AB2＝22＋22＝8.在△BCD中，因为BD2＋CD2＝8＋1＝9＝BC2，所以△BCD是直角三角形，且∠BDC＝90°.所以∠ADC＝∠ADB＋∠BDC＝45°＋90°＝135°.26.解：∵AD⊥BC,∴∠ADB=∠ADC=90°.在Rt△ADB中,∵∠B+∠BAD=90°,∠B=45°,∴∠B=∠BAD=45°,∴AB=BD=1,AB=.在Rt△ADC中,∵∠C=30°,∴AC=2AD=2,∴CD=,BC=BD+CD=1+, ∴AB+AC+BC=++3.27.解：设超市C与车站D的距离是x米，则AC＝CD＝x米，BC＝(BD－x)米，在Rt△ABD中，BD＝＝4000米，所以BC＝(4000－x)米，在Rt△ABC中，AC2＝AB2＋BC2，即x2＝30002＋(4000－x)2，解得x＝3125，因此该超市与车站D的距离是3125米28.解：∵a2＋b2＋c2＋50＝6a＋8b＋10c，∴a2＋b2＋c2－6a－8b－10c＋50＝0，即(a－3)2＋(b－4)2＋(c－5)2＝0，　∴a＝3，b＝4，c＝5.∵32＋42＝52，即a2＋b2＝c2，∴根据勾股定理的逆定理可判定△ABC是直角三角形．