八年级上数学课件八年级上册数学课件《勾股定理的图形验证》 北师大版 (2)_北师大版

八年级上数学课件八年级上册数学课件《勾股定理的图形验证》 北师大版 (2)_北师大版

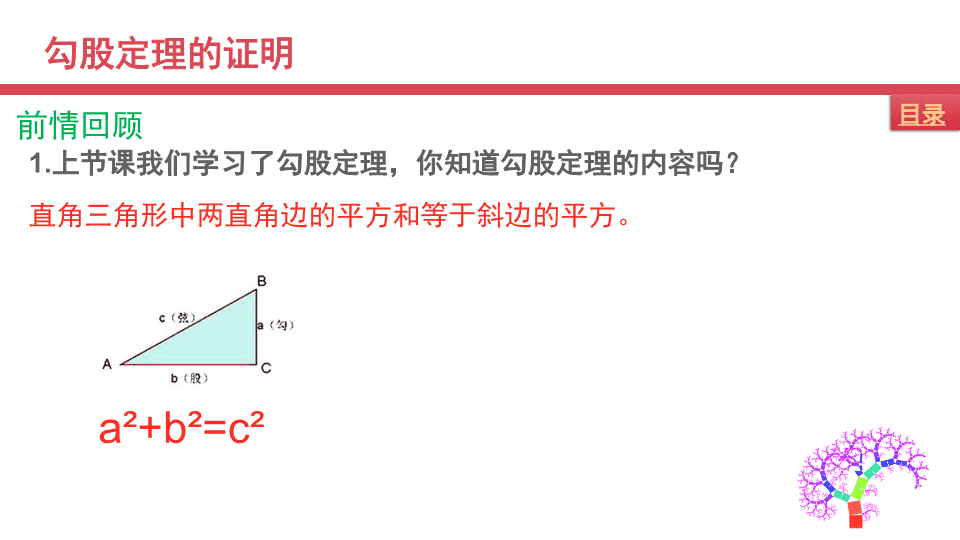
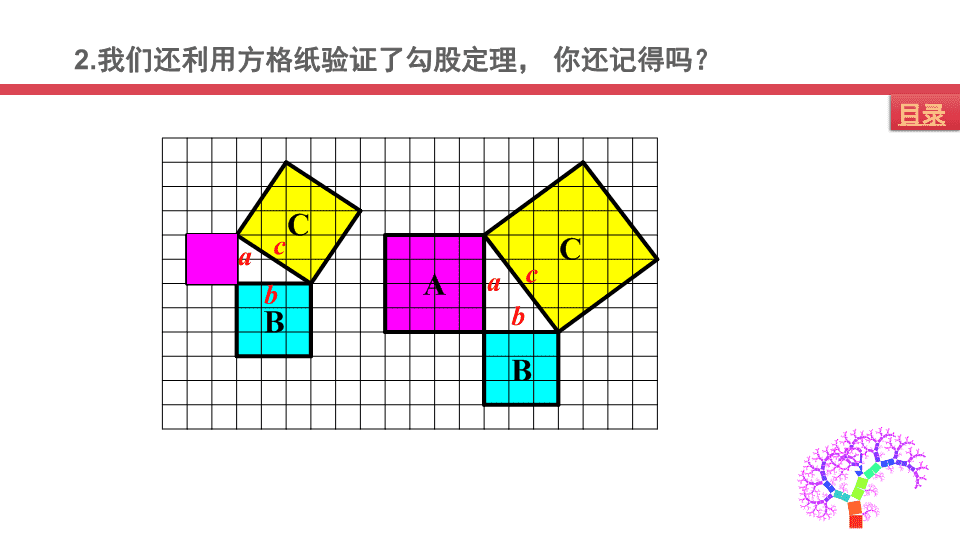
第一章勾股定理义务教育八年级数学（北师版）探究课：勾股定理的证明 勾股定理的证明1.上节课我们学习了勾股定理，你知道勾股定理的内容吗？直角三角形中两直角边的平方和等于斜边的平方。a²+b²=c²前情回顾 2.我们还利用方格纸验证了勾股定理，你还记得吗？abcabc 外弦图内弦图总统证法3.上节课的拓展作业是搜集有关勾股定理的发现、发展以及证明方法，你都搜到哪些资料了？能给我们分享一下吗？ 勾股定理的证明实验展示1：我们可以利用四个相等的直角三角形来拼成一个正方形.(1)bca(2)bca(3)bca(4)bca 勾股定理的证明实验论证：想一想我们还可以怎么拼？返回 勾股定理的证明实验展示2：我们还可以用这四个直角三角形卡片拼成一个更大的正方形(1)bca(2)bca(3)bca(4)bcababababa 勾股定理的证明实验论证：想一想我们还可以怎么拼？这种方法最先由邹元治提出返回 勾股定理的证明实验展示3：我们还可以用两个直角三角形来拼成一个直角梯形(1)bca(2)bcaaabbcc 勾股定理的证明实验论证：这种方法最先由1876年美国总统Garfield提出 勾股定理的证明想一想我们前面实验中是怎么证明勾股定理的呢？我们这种借助图形的面积来探索和验证数学结论的思想叫做数形结合的思想“数”与“形”反映了事物两个方面的属性。我们认为，数形结合，主要指的是数与形之间的一一对应关系。数形结合就是通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而实现优化解题途径的目的。 勾股定理的证明通过自己动手拼图和论证的过程，相信大家对勾股定理的证明有了更深入的了解。下面我们来介绍几种古代学者证明勾股定理的方法！一：青朱入出图二：达·芬奇的证明 青朱出入图三国时代魏国的数学家刘徽。在古籍《九章算术》作了注释。在注释中，他画了一个图形来证明勾股定理。由于他在图中以「青出」、「朱出」表示三个部分，又以「青入」、「朱入」解释如何将斜边正方形的空白部分填满，所以后世数学家都称这图为「青朱出入图」。也有人用「出入相补」这一词来表示这个证明的原理。你能看出来它是怎么证明勾股定理的吗？ 勾股定理的证明请同学们观看视频了解刘徽的证明方法我们可以发现刘徽是通过对图形的切割和补充来证明勾股定理的 达·芬奇的证明意大利文艺复兴时代的著名画家达·芬奇对勾股定理进行了研究。通过了解前面对勾股定理证明的思路，结合这个图形想一想通过怎么样的转变可以求证勾股定理！ 达·芬奇的证明过程详解：AaBCbDEFOⅠⅡA′B′C′D′E′F′ⅠⅡ 达·芬奇的证明a²+b²=c²现在你知道了达芬奇证明勾股定理的过程了吧，是不是为古代伟人的智慧所折服。证明过程：第一个多边形的面积与最后一个多边形面积相等。 勾股定理的证明课内练习11，如图是传说中验证勾股定理的一种方法，你能根据这两个图形及提示验证勾股定理吗？（提示：图①中拼成的大正方形与图②中拼成的大正方形面积相等） 勾股定理的证明证明过程：图①的面积为：图②的面积为：图①和图②面积相等得： 勾股定理的证明接下来我们来了解更多证明勾股定理的其他方法吧！(1)欧几里得《原本》(2)梅文鼎证明(3)利用相似三角形性质证明(4)作直角三角形的内切圆证明(5)利用切割线定理证明 勾股定理的证明课内练习2欣赏一颗美丽而神奇的树。它是由古希腊数学家毕达哥拉斯根据勾股定理所画出来的勾股定理树也称为“毕达哥拉斯树”。它使我们大家深刻的感受到了几何之美。在欣赏之余思考最外围所有小正方形的面积之和与哪个正方形的面积相等？希腊的著名数学家毕达哥拉斯发现了这个定理，因此世界上许多国家都称勾股定理为“毕达哥拉斯”定理。为了庆祝这一定理的发现，毕达哥拉斯学派杀了一百头牛酬谢供奉神灵，因此这个定理又有人叫做“百牛定理”． 勾股定理的证明我们可以先来看下列三个图形中最外围所有小正方形的面积之和与哪个正方形的面积相等。我们可以看到这三个图形的最外圈所有小正方形的面积之和都与最大的那个正方形面积相等。 勾股定理的证明由此我们可以推理归纳得到“毕达哥拉斯树”的最外围所有小正方形的面积之和也与那个最大的正方形面积相等。 课堂小结1、利用图形的摆拼验证勾股定理。2、体会“数形结合”的思想。 谢谢大家