八年级下数学课件八年级下册数学课件《一次函数》 人教新课标 (16)_人教新课标

八年级下数学课件八年级下册数学课件《一次函数》 人教新课标 (16)_人教新课标

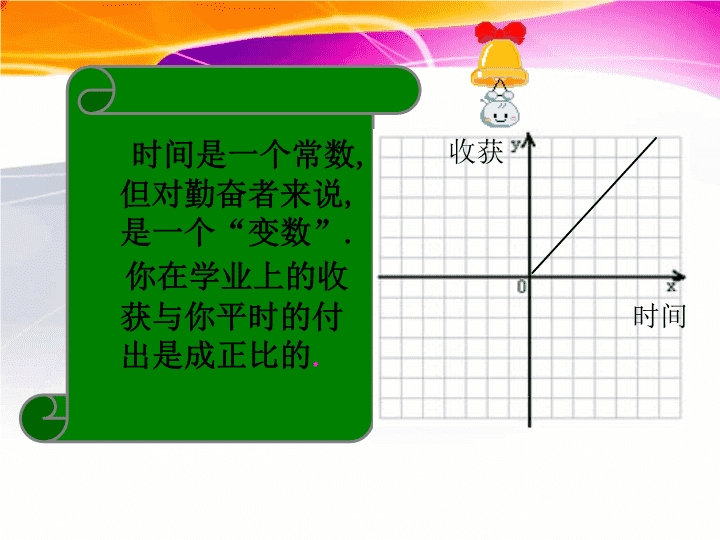
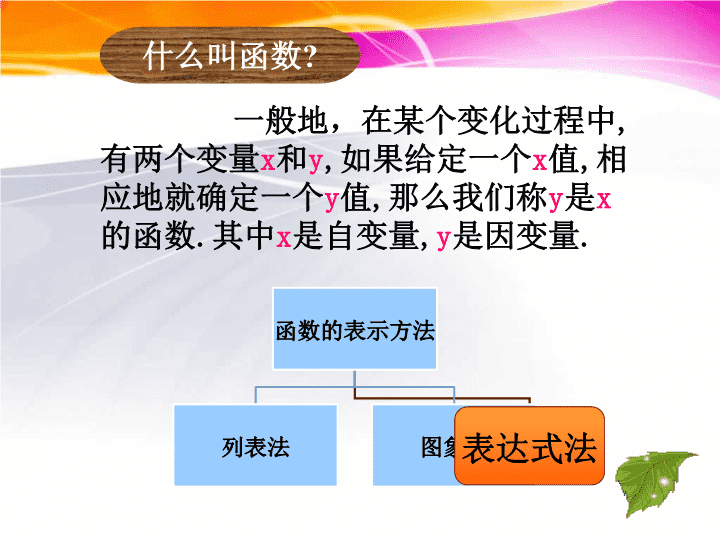
时间是一个常数,但对勤奋者来说,是一个“变数”.你在学业上的收获与你平时的付出是成正比的.收获时间 6.2一次函数北师大版八年级数学上册 一般地，在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数.其中x是自变量,y是因变量.什么叫函数?函数的表示方法列表法图象法表达式法 (6)某登山队大本营所在地的气温为50C，海拔每升高1km气温下降60C,登山队员由大本营向上登高xkm时,他们所在的位置的气温是y0C，试用解析式表示y与x的关系。分析:随变化的规律是，从大本营向上当海拔增加xkm时，气温从50C减少6x0C。因此y与x的函数关系式为:y=5–6x.解:y与x的函数关系y=-6x+5 (1)有人发现,在20~50℃时蟋蟀每分鸣叫的次数c与温度t(单位：℃)有关，即c的值约是t的7倍与35的差；(2)一种计算成年人标准体重G(单位：千克)的方法是，以厘米为单位量出身高值h，再减去常数105，所得差是G的值；(3)某城市的市内电话的月收费额y(单位：元)包括：月租费22元，拔打电话x分的计时费(按0.1元/分收取)；(4)把一个长10cm、宽5cm的长方形的长减少xcm,宽不变，长方形的面积y(单位：平方厘米)随x的值而变化C=7t-35G=h-105y=0.1x+22y=-5x+50思考：下列问题中的对应关系可用怎样的函数表示？这些函数有什么共同点？ 1.某弹簧的自然长度为3cm，在弹性限度内，所挂物体的质量x每增加1千克，弹簧长度y增加0.5cm.x/千克012345y/cm(2)你能写出y与x之间的关系吗？33.544.555.5y=3+0.5x做一做1(1)计算所挂物体的质量分别为1千克、2千克、3千克、4千克、5千克时的长度，并填入下表： 2.某辆汽车油箱中原有油100升,汽车每行驶50千米耗油9升.汽车行使路程x/千米050100150200300油箱剩余油量y/升1009182736446(2)你能写出y与x的关系吗?y=100－0.18x做一做2(1)完成下表： 议一议汽车行驶的路程x可以无限大吗?油箱剩余油量y呢? 分析：上面几个函数解析式有什么共同特征？1.y=0.5x+32.y=100-0.18x 当b=0时，称y＝kx是x的正比例函数一次函数：若两个变量x、y之间的关系可以表示成y=kx+b(k,b为常数，k≠0）的形式，则称y是x的一次函数。（x为自变量，y为因变量）又获新知正比例函数是特殊的一次函数！ 判断下列各式中X与Y之间的函数关系（1）y=-x-4它是一次函数，不是正比例函数。它不是一次函数，也不是正比例函数。它是一次函数，也是正比例函数。它不是一次函数，也不是正比例函数。练一练1（2）y=x2（3）y=2πx（4）y=1—x 3.已知函数y=(m+1)x+(m2-1),当m取什么值时，y是x的一次函数？当m取什么值时，y是x的正比例函数？应用拓展解：（1）因为y是x的一次函数所以m+1≠0m≠-1（2）因为y是x的正比例函数所以m2-1=0m=1或-1又因为m≠-1所以m=1 在平面直角坐标系中画出函数的图象。xy002…-2-1……-1-0.50.51…●●●●●同一条直线上直线描出以上各点后，我们会发现这些点在____________。即函数的图象是一条______。并且经过点（__，__），即_____。是不是所有的一次函数的图象都是直线呢？我们在起先的坐标系中再来画函数的图象。00原点 x在平面直角坐标系中画出函数的图象。0…-2-112…0…-1-0.50.51…22.53…11.5…我们可以发现：函数的图象也是一条直线。其实，所有一次函数y=kx+b的图象都是一条直线，并且k和b的值将决定其图象的位置和特点哦。 我们已经知道：一次函数y=kx+b的图象是_______。那么，一条直线由几个点可以确定呢？_________。所以，我们今后在列表画一次函数的图象只要选取____个点就可以了。直线两个点两 一、创设情境1.一次函数的图象是一条直线，一般情况下我们画一次函数的图象，取哪两个点比较简便？（0，b)和（-b/k,0) 观察函数的解析式及其图象，填写下表。y=3xy=3x+2解析式图象y=3xy=3x+2相同点：________。不同点：________。相同点：________________________________________________不同点：________________________相同点：________。不同点：________。相同点：________________________________________________不同点：________________________y=3x+2相同点：________。不同点：________。相同点：________________________________________________。不同点：________________________。k相同b不同k相同b不同倾斜度一样（平行）都经过一、三象限直线y=3x+2还经过第二象限倾斜度一样（平行）都经过一、三象限直线还经过第二象限b相同k不同都与y轴相交于点（0，2）都经过一、二、三象限倾斜度不一样（不平行） y=3xy=3x+2观察函数y=3x和y=3x+2的图象，我们知道：它们是互相平行的，所以，其中一条直线可以看作是由另一条直线平移得到的。你能说出直线y=3x+2是由直线y=3x向____平移____个单位得到的吗？上2如果直线y=3x向下平移1个单位，那么，可以得到直线_________。提示：关键是确定y=kx+b中b的值。y=3x-1 例题：已知一次函数的图象经过点(3,5)与（－4，－9）.求这个一次函数的解析式．解：设这个一次函数的解析式为y=kx+b.∵y=kx+b的图象过点（3，5）与（-4，-9）.∴3k+b=5-4k+b=-9解得k=2b=-1∴这个一次函数的解析式为y=2x-1像这样先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法，叫做待定系数法.初步应用，感悟新知设代求写 一次函数图象和性质y=kx+b图象性质直线经过的象限增减性K>0b=0b>0b<0第一、三象限y随x增大而增大第一、二、三象限y随x增大而增大第一、三、四象限y随x的增大而增大yx0(0,b)yx0(0,b)yx0 y=kx+b图象性质直线经过的象限增减性K<0b=0b>0b<0第二、四象限y随x增大而减小第一、二、四象限y随x增大而减小第二、三、四象限y随x增大而减小y0x(0,b)xy0(o,b)xy0 例1写出下列各题中y与x之间的关系式，并判断：y是否为x的一次函数？是否为正比例函数？练一练2（1）汽车以60千米/时的速度匀速行驶,行驶路程为y(千米)与行驶时间x(时)之间的关系;（2）圆的面积y(厘米2)与它的半径x(厘米）之间的关系.（3）一棵树现在高50厘米，每个月长高2厘米，x月后这棵树的高度为y厘米. 解：由圆的面积公式，得y=πx2,y不是x的正比例函数，也不是x的一次函数.解：这棵树每月长高2厘米，x个月长高了2x厘米，因而y=50+2x,y是x的一次函数，但不是x的正比例函数.练一练2解：由路程=速度×时间，得y=60x，y是x的一次函数,也是x的正比例函数. 例2：我国现行个人工资、薪金所得税征收办法规定：月收入低于1600元的部分不收税：月收入超过1600元但低于2100元的部分征收5%的所得税……如某人月收入1960元，他应缴个人工资、薪金所得税为（1960-1600）×5%=18（元）.（1）当月收入大于1600元而又小于2100元时，写出应缴所得税y（元）与月收入x（元）之间的关系式.解：当月收入大于1600元而小于2100时，y=0.05×(x-1600).试一试 (2)某人月收入为1760元，他应缴所得税多少元？解：当x=1760时，y=0.05×(1760-1600)=8（元）.试一试例2：我国现行个人工资、薪金所得税征收办法规定：月收入低于1600元的部分不收税：月收入超过1600元但低于2100元的部分征收5%的所得税……如某人月收入1960元，他应缴个人工资、薪金所得税为（1960-1600）×5%=18（元）. (3)如果某人本月应缴所得税19.2元，那么此人本月工资、薪金是多少元？解：设此人本月工资、薪金是x元，则19.2=0.05×(x-1600),解得：x=1984.即本月工资、薪金是1984元.例2：我国现行个人工资、薪金所得税征收办法规定：月收入低于1600元的部分不收税：月收入超过1600元但低于2100元的部分征收5%的所得税……如某人月收入1960元，他应缴个人工资、薪金所得税为（1960-1600）×5%=18（元）. 练一练31、某种大米的单价是2.2元/千克，当购买x千克大米时，花费为y元，y是x的一次函数吗？是正比例函数吗？解：y=2.2x，y是x的一次函数，也是x的正比例函数。 2、如图，甲乙两地相距100千米，现有一列火车从乙地出发，以80千米/时的速度驶向甲地。设x（时）表示火车行驶的时间，y（千米）表示火车与甲地的距离，写出y与x之间的关系式，并判断y是否是x的一次函数？练一练3解：y=80x+100，y是x的一次函数。甲乙丙 同学们，本节课你有哪些收获？能和别人分享吗？ 1、习题6.2：2、3题2、读一读：漏刻布置作业 读一读漏刻是我国古代发明的一种计时工具,它是劳动人民的智慧结晶，也是一次函数的一次创造性地使用.请读一读教材课后阅读资料或上网查阅相关材料． 结束寄语时间是一个常数,但对勤奋者来说,是一个“变数”.你在学业上的收获与你平时的付出是成正比的.收获时间