八年级下数学课件八年级下册数学课件《特殊的平行四边形》 人教新课标 (3)_人教新课标

八年级下数学课件八年级下册数学课件《特殊的平行四边形》 人教新课标 (3)_人教新课标

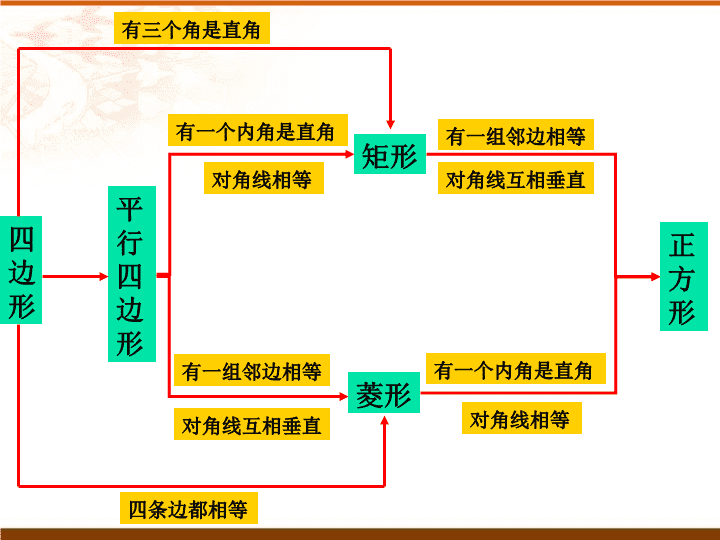
特殊平行四边形 一、复习目标矩形、菱形、正方形①了解平行四边形、矩形、菱形、正方形的关系a②掌握矩形、菱形、正方形的概念b③探索并掌握矩形、菱形、正方形的有关性质c④探索并掌握四边形是矩形、菱形、正方形的条件c⑤知道任意一个三角形、四边形或正方形可以镶嵌平面，并运用这几种图形进行简单的镶嵌设计b 平行四边形四边形矩形菱形正方形有一个内角是直角对角线相等有一组邻边相等对角线互相垂直四条边都相等有三个角是直角有一组邻边相等对角线互相垂直有一个内角是直角对角线相等 二、知识概要性质判定边两组对边分别平行两组对边分别相等有一个角是直角的平行四边形是矩形角矩形的四个角都是直角有三个角是直角的四边形是矩形对角线矩形的两条对角线相等对角线相等的平行四边形是矩形推论直角三角形斜边上的中线等于斜边的一半如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形(矩形) 二、知识概要性质判定边菱形的四条边都相等.①一组邻边相等的平行四边形是菱形.②四条边都相等的四边形是菱形.角①对角相等.②邻角互补.对角线菱形的两条对角线互相垂直；并且每条对角线平分一组对角.对角线互相垂直的平行四边形是菱形.(菱形) 二、知识概要性质判定边正方形的四条边都相等.有一组邻边相等的矩形是正方形.角正方形的四个角都是直角.有一个角是直角的菱形是正方形.对角线正方形的两条对角线相等.并且互相垂直平分.每条对角线平分一组对角.①对角线相等的菱形是正方形.②对角线互相垂直的矩形是正方形.(正方形) 三、基本练习(填空题)1.如图，根据四边形的不稳定性制作边长为16cm的可活动的菱形衣架，若墙上钉子间的距离AB=BC=16cm，则∠1=_____度。2.已知，矩形ABCD的长AB=4，宽AD=3，按如图放置在直线AP上，然后不滑动转动，当它转动一周时（A→A′），顶点A所经过的路线长等于________。1206π 三、基本练习(填空题)3.如图，已知正方形纸片ABCD，M，N分别是AD，BC的中点，把BC向上翻折，使点C恰好落在MN上的P点处，BQ为折痕，则∠PBQ=________度。30 三、基本练习(选择题)1.如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D’处，那么tan∠BAD′等于（）(A)1(B)(C)(D)22.矩形ABCD的顶点A，B，C，D按照顺时针方向排列，若在平面直角坐标系中，B，D两点对应的坐标分别是（2，0），（0，0），且A，C两点关于x轴对称，则C点对应的坐标是（）(A)(1,1)(B)(1,-1)(C)(1,-2)(D)(,-)BB (选择题)3.如图，有一块矩形纸片ABCD，AB=10，AD=6，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为（）(A)4(B)6(C)8(D)10C三、基本练习 例1.工人师傅做铝合金窗框分下面三个步骤进行:（1）先截出两对符合规格的铝合金窗料，使AB=CD，EF=GH. 例1.工人师傅做铝合金窗框分下面三个步骤进行:（2）摆成如图所示的四边形，则这时窗框的形状是，根据的数学道理：。平行四边形两组对边分别相等的四边形是平行四边形 例1.工人师傅做铝合金窗框分下面三个步骤进行:（3）将直角尺靠紧窗框的一个角，调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时，说明窗框合格，这时窗框是形，根据的数学道理是。矩有一个角是直角的平行四边形是矩形 还有什么方法可以说明这个铝合金窗框是合格的?想一想ABCDABCDAC=BD∠A=∠B=∠C=90° ABCDo60若这个铝合金窗框ABCD两条对角线的夹角∠AOB为60°，△AOB的周长为3m。（1）求窗框对角线AC长； ABCDo60若这个铝合金窗框ABCD两条对角线的夹角∠AOB为60°，△AOB的周长为3m。（2）求窗框ABCD的面积。 例2.如图，两张等宽的纸条交叉重叠在一起，猜想重叠部分的四边形ABCD是什么形状？说说你的理由。FE 例3.将一张矩形的纸对折再对折，然后沿着图中的虚线剪下，打开，你会发现这是一个菱形。你能解释其中的道理吗？ 若展开后的菱形纸片ABCD中，两条对角线AC=，BD=4。（1）求菱形ABCD的面积；（3）求∠ADC的度数。（2）求菱形ABCD的周长； 如果想得到一个正方形，该怎么剪？并解释你这样做的道理。想一想 例4.已知正方形ABCDABCD（1）若一条对角线BD长为2cm，求这个正方形的周长、面积。 例4.已知正方形ABCDABCD（2）若E为对角线上一点，连接EA、EC。EA=EC吗？说说你的理由。E 例4.已知正方形ABCD（3）若AB=BE，求∠AED的大小。ABCDE 例5.顺次连接任意四边形各边的中点，所构成的四边形以下简称为“中点四边形”。试判断中点四边形EFGH的形状，并说明理由。（1）添加一个条件，使四边形EFGH为菱形；AC⊥BDAC=BDAC=BD且AC⊥BD（2）添加一个条件，使四边形EFGH为矩形；（3）添加一个条件，使四边形EFGH为正方形； 1.矩形的“中点四边形”是形；2.菱形的“中点四边形”是形；3.正方形的“中点四边形”是形。矩菱正方那么，特殊平行四边形的“中点四边形”会是怎样的图形呢？ 中考链接1.（河北省2005）如图，在矩形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点。若AB=2，AD=4，则阴影部分的面积为（）346D.8B. 中考链接2.（陕西省2005）如图，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD的面积比是（）3：45：89：16D.1：2B. 3.已知正方形ABCD，ME⊥BD，MF⊥AC，垂足分别为E、F（1）M是AD上的点，若对角线AC=12cm，求ME+MF的长。ABCDOMFE（2）若M是AD上的一个动点，ME+MF的长度是否发生改变？（3）当M点运动到何处时，四边形MFOE的面积最大？ 1.如图，正方形MNPQ网格中，每个小方格的边长都相等，正方形ABCD的顶点分别在正方形MNPQ的4条边的小方格的顶点上。（1）设正方形MNPQ网格中每个小方格的边长为1，求：①△ABQ,△BCM,△CDN,△ADP的面积②正方形ABCD的面积（2）设MB=a，BQ=b，利用这个图形中直角三角形和正方形的面积关系，你能验证已学过的哪一个数学公式或定理吗？相信你能给出简明的推理过程。四、训练题 2.如图，在△ABC中，∠ACB=90°，BC的中垂线DE交BC于点D,交AB于点E，F在DE的延长线上，并且AF=CE.（1）证明：四边形ACEF是平行四边形.（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论.（3）四边ACEF有可能是正方形吗？请证明你的结论。 3.探究下列问题：（1）如图①，在△ABC中，CP⊥AB于点P，求证:AC2-BC2=AP2-BP2；（2）如图②，在四边形ABCD中，AC⊥BD,垂足为P，猜一猜AB,BC,CD,DA之间有何数量关系，用式子表示出来（不必说明理由）；（3）如图③，在矩形ABCD中，P为内部任意一点，请猜想出AP,BP,CP,DP之间的数量关系，并证明之。 4.如图，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴上，点C在y轴上，OA=10，OC=6。（1）如图①，在OA上选取一点G，将△COG沿CG翻折，使点O落在BC边上，设为E，求折痕CG所在直线的解析式。 4.（2）如图②，在OC上任取一点D，将△AOD沿AD翻折，使点O落在BC边上，记为E’。①求折痕AD所在直线的解析式；②再作E’F//AB，交AD于点F，若抛物线过点F，求此抛物线的解析式，并判断它与直线AD的交点的个数。 4.（3）如图③，在OC，OA上选取适当的点D’，G’，使纸片沿D’G’翻折后，点O落在BC边上，记为E’’。请你猜想：折痕D’G’所在直线与②中的抛物线会用什么关系？用（1）中的情形验证你的猜想。 5.正方形通过剪切可以拼成三角形（如图①）。方法如下：仿上例用图示的方法，解答下列问题：操作设计：（1）如图②，对直角三角形，设计一种方案，将它分成若干块，再拼成一个与原三角形等面积的矩形。（2）如图③，对任意三角形，设计一种方案，将它分成若干块，再拼成一个与原三角形等面积的矩形。（3）对于任意四边形，能否通过恰当的分割和重新组合拼接，使其成为一个与四边形等面积的矩形。