八年级下数学课件：17-1 勾股定理 （共16张PPT）2_人教新课标

八年级下数学课件：17-1 勾股定理 （共16张PPT）2_人教新课标

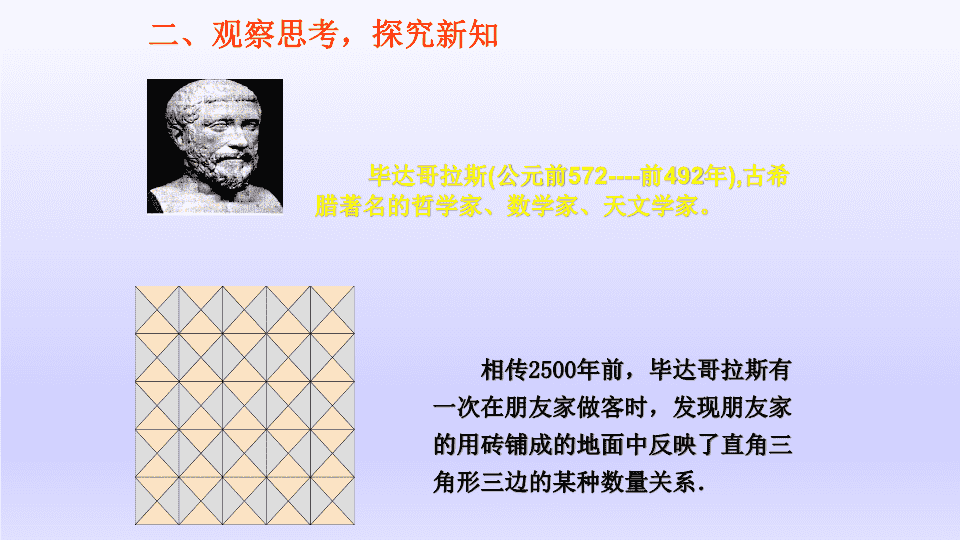
17.1勾股定理新人教版八年级下册 它由哪些我们学过的基本图形组成？这些图形的边之间有哪些关系，面积怎样计算？为什么选用这个图案做为2002年国际数学家大会的会徽呢？ 毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。二、观察思考，探究新知相传2500年前，毕达哥拉斯有一次在朋友家做客时，发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系． 1.问题：A、B、C的面积有什么关系？SA+SB=SCABC对于等腰直角三角形三边有这样的关系：两条直边的平方和等于斜边的平方ABC ABC图乙91625448ABC图甲图甲图乙A的面积B的面积C的面积CSA+SB=SC2.问题：观察图甲、图乙，小方格的边长为1.正方形A、B、C的面积有什么关系？a2+b2=c2abcabc 3.探究总结，提出猜想命题１：如果直角三角形的两直角边长分别为a、b，斜边长为c，那么a2+b2=c2cab a2+b2=c2证法：赵爽弦图4.证明命题1小组讨论，通过割补拼一个正方形，探究a、b、c之间的关系。小组展示，并请3位同学拿着图形表演： 5.命题正确，总结定理在西方国家又称为毕达哥拉斯定理！即：直角三角形两直角边的平方和等于斜边的平方。勾股定理：如果直角三角形两直角边分别为a、b,斜边为c，那么.abc弦勾股“赵爽弦图”，它通过对图形的切割、拼接，巧妙地利用面积关系证明了勾股定理，它表现了我国古人对数学的钻研精神和聪明才智，是我国古代数学的骄傲。因此，这个图案被选为2002年在北京召开的国际数学家大会的会徽。 勾股定理给出了直角三角形三边之间的关系，即两直角边的平方和等于斜边的平方.cbaa2+b2=c2a2=c2－b2b2=c2-a26.公式变形，灵活运用 1.求出下列直角三角形中未知边的长度：68x5x13解：由勾股定理得：∴x2=36+64x2=100∵x2=62+82x=10∵x2+52=132∴x2=132-52x2=169-25x2=144x=12解：由勾股定理得：提示：根据勾股定理，已知直角三角形任意两条边的长，可以求第三条边的长。(1)(2)三、运用公式，巩固新知 2.求下列直角三角形中未知边的长:提示：可用勾股定理建立方程求解.8x1732x63x(1)(2)(3) 四、参与活动，加强运用1.活动规则：6个小组进行比赛，每个小组派一个代表参加比赛，哪个小组算得又快又对就获胜。题目：设直角三角形的两条直角边为a和b，斜边为c.(1)已知a=6，c=10,求b;(2)已知a=5，b=12,求c;(3)已知b=15，c=25,求a;(4)已知a=3，c=4,求b;(5)已知b=2，c=7,求a;(6)已知a=4，b=5,求c. 2.编题目游戏，考一考你的同学游戏要求：每一位同学画一个直角三角形，给出任意两条边的长，求第三条边x.然后小组之间每两个同学交换解答，再交换回来批改，看看你的同学是否会学会运用勾股定理，如果他（她）不会，请你教教他（她）.最后由各小组长汇报游戏情况.例如：35x 这节课，你的收获是什么？五、课堂小结，谈谈收获（1）了解了勾股定理的历史故事；（2）知道了直角三角形三边的等量关系；（3）记住了勾股定理；（4）懂得了勾股定理的证明方法；（5）会运用勾股定理进行简单的计算；....... 课本第28页，习题17.1的第1题.六、布置作业 谢谢再见！