八年级上数学课件八年级上册数学课件《平面直角坐标系》 北师大版 (9)_北师大版

八年级上数学课件八年级上册数学课件《平面直角坐标系》 北师大版 (9)_北师大版

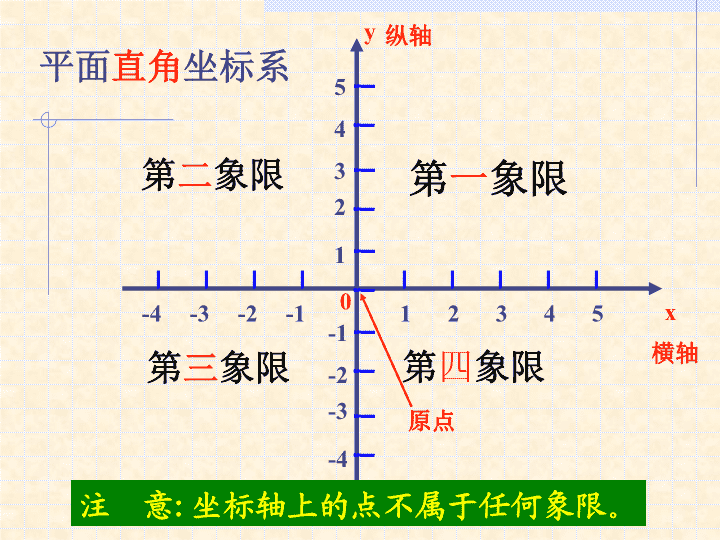
5.2平面直角坐标系 学习目标：（1）理解平面直角坐标系的有关概念，能正确画出直角坐标系。（2）能在平面直角坐标系中，根据坐标找出点，由点求出坐标。(3)了解平面内的点与有序实数对之间的一一对应关系。学习重点：平面直角坐标系及其有关概念，根据坐标找点，由点求坐标。学习难点：坐标平面内特殊位置的点的坐标特征。 012345-4-3-2-131425-2-4-1-3平面直角坐标系x横轴y纵轴第一象限第二象限第三象限第四象限注意:坐标轴上的点不属于任何象限。原点 ·A31425-2-4-1-3012345-4-3-2-1x横轴y纵轴A点在x轴上的坐标为3，即横坐标为3A点在y轴上的坐标为2，即纵坐标为2A点在平面直角坐标系中的坐标为(3,2)记作：A（3，2）X轴上的坐标写在前面·BB（-4，1）确定点A在平面内的位置 ·B31425-2-4-1-3012345-4-3-2-1y纵轴·C·A·E·D(2，3)(3，2)(-3，2)(-4，0)(2，-3)例1、写出图中A、B、C、D、E、F、G各点的坐标。x横轴坐标是有序的实数对。x横轴·F(0，5)·G(-3，-2) B31425-2-4-1-3012345-4-3-2-1y纵轴C·A·E·D(2，3)(3，2)(-3，2)(-4，0)(2，-3)x横轴·F(0，5)··1、x轴上点的坐标.2、y轴上点的坐标.3、原点坐标.3、第一象限点的坐标.4、第二象限点的坐标.5、第三象限点的坐标.6、第四象限点的坐标.·G(-3，-2)(x，0)(0，y)(+，+)(-，+)(-，-)(+，-)(0，0)观察各点坐标回答问题··· 31425-2-4-1-3012345-4-3-2-1x横轴y纵轴·F例2、在直角坐标系中，描出下列各点：A（4，5）、B（-2，3）、C（-4，-1）、D（2.5，-2）、E（0，-4）、F（4，3） 练一练若点A（a,b）在第三象限，则点Q(－a+1，b－5)在第（）象限。2.若点B（m+4,m－1)在X轴上，则m=______。3.若点C(x,y)满足x+y<0,xy>0，则点C在第（）象限。四1三 3142-2-1-3012345-4-3-2-1xy·Po·Px4、点P（4，-3）关于X轴对称的点的坐标是：关于Y轴对称的点的坐标是：关于原点对称的点的坐标是：P·Py·（4，3）（-4，-3）（-4，3） 1、点P(a，b)关于X轴对称的点的坐标是：关于Y轴对称的点的坐标是：关于原点对称的点的坐标是：3142-2-1-3012345-4-3-2-1xy·Po·PxPPy（a，-b）（-a，b）（-a，-b）总结升华·2、横坐标相同的点连线纵坐标相同的点连线平行y轴平行x轴· 练一练:⑴已知点P1(a，3)与点P2(-2，b)关于Y轴对称，则a=(),b=()⑵已知点P1(a，3)与点P2(-2，b)关于X轴对称，则a=(),b=()⑶已知点P1(a，3)与点P2(-2，b)关于原点对称，则a=(),b=()23-2-32-3 讲学稿能力提升5、解：做DE⊥AB于E，CF⊥AB于F由题意可知AE=1，DE=3，CF=4，BF=2，EF=5S四边形ABCD=S△ADE+S△CEF+S梯形EFCD==23ABCDEF 讲学稿聚沙成塔●●●0解、做点A关于x轴的对称点C，连接BC，则BC为所求最小值。由题意可知BD=4，CD=1，∴BC=即PA+PB的最小值为。ABCD 学习本节我们要掌握以下三方面的内容：1、能在直角坐标系中，根据坐标找出点，由点求出坐标。2、坐标平面分为哪几部分？各有什么特征？3、对称点的坐标有何规律？小结谈谈你有哪些收获？