八年级上数学课件- 14-2-2 完全平方公式 课件（共15张PPT）_人教新课标

八年级上数学课件- 14-2-2 完全平方公式 课件（共15张PPT）_人教新课标

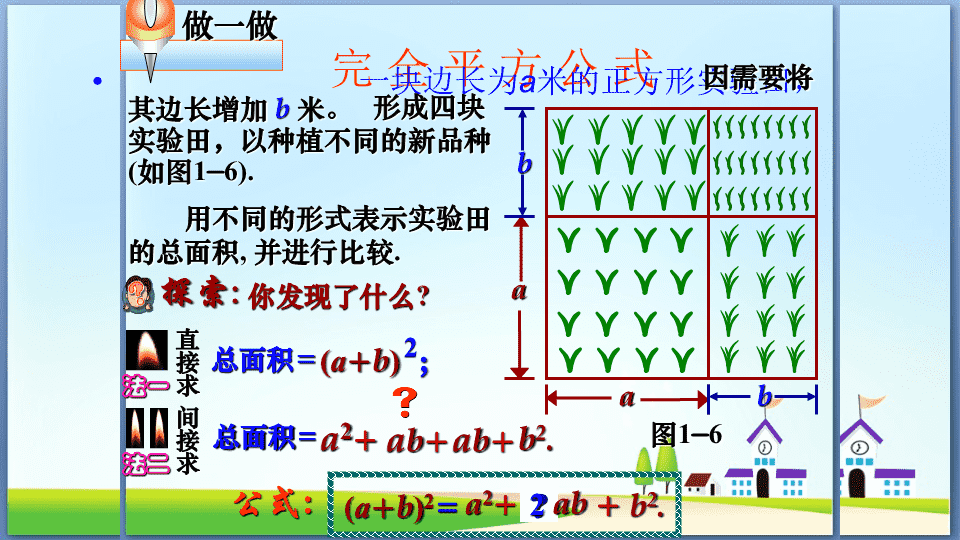
15.2.2完全平方公式人教版八年级(上) 回顾与思考公式的结构特征:左边是a2−b2;两个二项式的乘积,应用平方差公式的注意事项:对于一般两个二项式的积,看准有无相等的“项”和符号相反的“项”;仅当把两个二项式的积变成公式标准形式后，一定要用符号相同“项”的平方减符号相反“项”的平方。温故&知新☞(a+b)(a−b)=即两数和与这两数差的积.右边是两数的平方差.☾弄清在什么情况下才能使用平方差公式:在解题过程中要准确确定a和b、对照公式原形的两边,做到不弄错符号、当第一(二)数是乘积且被平方时要注意添括号,是运用平方差公式进行多项式乘法的关键。平方差公式: 完全平方公式一块边长为a米的正方形实验田，做一做图1—6a因需要将其边长增加b米。形成四块实验田，以种植不同的新品种(如图1—6).用不同的形式表示实验田的总面积,并进行比较.abb法一直接求总面积=(a+b)；2法二间接求总面积=a2+ab+ab+b2.(a+b)2=a2+ab+b2.你发现了什么?探索:2公式: 完全平方公式开动脑筋(1)你能用多项式的乘法法则来说明它成立吗?想一想(a+b)2=a2+2ab+b2;(a+b)2=推证(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2;(2)a2−2ab+b2.张亮写出了如下的算式:(a−b)2=[a+(−b)]2(a−b)2=他是怎么想的?利用两数和的完全平方公式推证公式(a−b)2=[a+(−b)]2=2+2+2aa(−b)(−b)=a22ab−b2.+你能继续做下去吗?的证明 掀起你的盖头来---完全平方公式什么时候用加，什么时候用减呢(a+b)2=a2+2ab+b2.(a−b)2=a2−2ab+b2.结构特征:左边是的平方;二项式右边是a2+b2a2+b2(两数和)(差)a+ba−b这两数的平方和+加上−(减去)2ab2ab这两数乘积的两倍.22(a−b)2=a2−2ab+b2注意事项: 让我们的大脑开足马力回答下列问题:(1)(a+2y)2是哪两个数的和的平方?(a+2y)2=()2+2()()+()2(2)(2m−3n)2是哪两个数的差的平方?(2m-3n)2=()2-2()()+()2aa2y2y2m2m3n3n(2m−3n)2可以看成2m与−3n的和的平方.(2m−3n)2可以看成哪两个数的和的平方? 真金不怕火炼例1利用完全平方公式计算：(1)(4m+n)2；(2)(a−b)2;(3)(b-a)2解:(1)(4m+n)2=4m(4m)2nn22×4m×n++=16m2+8mn+n2(2)(a−b)2=a2-2•a•b+b2=a2-2ab+b2(3)(b-a)2=b2-2•b•a+a2=b2-2ab+a2(a+b)2=a2+2ab+b2.(a−b)2=a2−2ab+b2.这与(a-b)2=a2−2ab+b2(b−a)2=b2−2ab+a2有何关系(a−b)2=(b-a)2 随堂练习随堂练习(1)(x+6)2；(2)(y-5)2;(3)(-2x+5)2;(4)(x-y)21、计算： 例题解析例题学一学例2运用完全平方公式计算：(1)1022；(2)992解:(1)1022=(100+2)2变形(2)992==1002+2×100×2+22=10000+400+4=10404(100-1)2=1002-2×100×1+12=10000-200+1=98012、准确代入公式;利用完全平方公式计算:1、先选择公式;3、化简. 指出下列各式中的错误，并加以改正：(1)(2a−1)2＝2a2−2a+1;(2)(2a+1)2＝4a2+1；(3)(a−1)2＝a2−2a−1.解:(1)第一数被平方时,未添括号;第一数与第二数乘积的2倍少乘了一个2;应改为:(2a−1)2＝(2a)2−2•2a•1+1;(2)少了第一数与第二数乘积的2倍(丢了一项);应改为:(2a+1)2＝(2a)2+2•2a•1+1;(3)第一数平方未添括号,第一数与第二数乘积的2倍错了符号;第二数的平方这一项错了符号;应改为:(a−1)2＝(a)2−2•(a)•1+12;火眼金睛——辨是非 基础练习综合运用拓广探索学以致用—分层练习亲爱的同学们，请你根据自己对本节内容掌握的程度选择相应难度的练习进行训练。 1.下列运用完全平方公式计算正确的是（）A(x+y)2=x2+y2B(x-y)2=x2−2xy−y2C(x+2y)2=x2+4xy+2y2D(-x+y)2=x2−2xy+y22.利用完全平方公式计算：（1）(4x-3y)2（2）632基础练习： 1.如果x2+mx+4是一个完全平方公式，那么m的值是（）A．4B．-4C．±4D．±82.利用公式计算：（1）(3x−5)2−(2x+7)2；（2）(m−n+3)2综合运用：c 1.将正方形的边长由acm增加6cm，则正方形的面积增加了（）A．36cm2B．12acm2C．（36+12a）cm2D．以上都不对2.已知a+b=5，ab=3，求a2+b2的值。拓广探索：c3.已知：求：的值。 本节课你的收获是什么？小结本节课你学到了什么?注意完全平方公式和平方差公式不同：形式不同．结果不同：完全平方公式的结果是三项，即(ab)2＝a22ab+b2;平方差公式的结果是两项，即(a+b)(a−b)＝a2−b2.有时需要进行变形，使变形后的式子符合应用完全平方公式的条件，即为“两数和(或差)的平方”，然后应用公式计算.在解题过程中要准确确定a和b、对照公式原形的两边,做到不丢项、不弄错符号、2ab时不少乘2；第一(二)数是乘积被平方时要注意添括号,是运用完全平方公式进行多项式乘法的关键