八年级下数学课件八年级下册数学课件《三角形的中位线》 北师大版 (3)_北师大版

八年级下数学课件八年级下册数学课件《三角形的中位线》 北师大版 (3)_北师大版

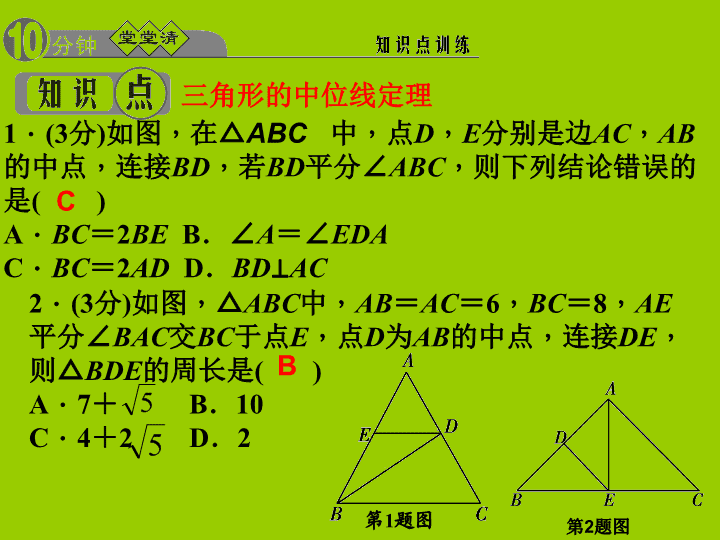
三角形的中位线 6.3三角形的中位线得分________卷后分________评价________1．连接三角形两边中点的线段叫做．2．三角形的中位线平行于，且等于．第三边第三边的一半三角形的中位线 三角形的中位线定理1．(3分)如图，在△ABC中，点D，E分别是边AC，AB的中点，连接BD，若BD平分∠ABC，则下列结论错误的是()A．BC＝2BEB．∠A＝∠EDAC．BC＝2ADD．BD⊥AC第1题图第2题图2．(3分)如图，△ABC中，AB＝AC＝6，BC＝8，AE平分∠BAC交BC于点E，点D为AB的中点，连接DE，则△BDE的周长是()A．7＋B．10C．4＋2D．2BC 3．(3分)如图，在四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP上的中点，当点P在CD上从点C向点D移动而点R不动时，那么下列结论成立的是()A．线段EF的长逐渐增大B．线段EF的长逐渐减小C．线段EF的长不变D．线段EF的长与点P的位置有关4．(3分)在△ABC中，D，E，F分别是AB，BC，AC的中点，若△ABC的周长为20cm，则△DEF的周长为()A．5cmB．10cmC．12cmD．15cm第3题图CB 5．(3分)如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，点E，F，G，H分别是AB，AC，CD，BD的中点，则四边形EFGH的周长是()A．7B．9C．10D．11第5题图D6．(3分)如图，点D，E，F分别是△ABC的边AB，BC，CA的中点，连接DE，EF，FD，则图中平行四边形的个数是____．7．(3分)如图，在▱ABCD中，AC，BD相交于点O，点E是AB的中点，OE＝3cm，则AD的长是____cm.8．(3分)顺次连接四边形各边的中点得到的四边形是．第7题图第6题图3个6平行四边形 9．(8分)如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD＝BC，∠PEF＝18°，求∠PFE的度数．10．(8分)如图，在△ABC中，D，E，F分别为AB，BC，CA的中点．求证：四边形DECF是平行四边形．解：∠PFE＝18°∥解：∵E为BC的中点，∴EC＝BC，又∵D，F分别是AB，AC的中点，∴DF为△ABC的中位线，∴DF＝BC且DF∥BC∴DFEC，∴四边形DECF是平行四边形 一、选择题(每小题3分，共12分)11．直角三角形两直角边的长分别为3和4，则连接这两条直角边的中点的线段长为()A．1.5B．2C．2.5D．512．如图，在△ABC中，M是BC边的中点，AD是∠A的平分线，BD⊥AD于点D，AB＝12，AC＝22，则MD的长为()A．3B．4C．5D．6第12题图CC 13．三角形三条中位线的长分别为3，4，5，则此三角形的面积为()A．12B．24C．36D．4814．(2014·枣庄)如图，△ABC中，AB＝4，AC＝3，AD，AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为()第14题图BA 二、填空题(每小题3分，共12分)15．如图所示，要测量A，B两点间距离，在点O打桩，取OA的中点C，OB的中点D，测得CD＝30米，则AB＝____米．第15题图16．如图，杨伯家小院子的四棵小树E，F，G，H刚好在其梯形院子ABCD各边的中点上，若在四边形EFGH上种小草，则这块草地的形状是．17．(2014·永州)如图，已知直线l1：y＝k1x＋4与直线l2：y＝k2x－5交于点A，它们与y轴的交点分别为点B，C，点E，F分别为线段AB，AC的中点，则线段EF的长度____．第17题图第16题图60平行四边形 18．如图，在△ABC中，EF为△ABC的中位线，D为BC边上一点(不与B，C重合)，AD与EF交于点O，连接DE，DF，要使四边形AEDF为平行四边形，需要添加的条件是．(只添加一个条件)第18题图AD为△ABC的中线(答案不唯一)19．(8分)如图，在△ABC中，AB＝BC＝12cm，∠ABC＝80°，BD是∠ABC的平分线，DE∥BC.(1)求∠EDB的度数；(2)求DE的长．解：(1)∠EDB＝40°(2)DE＝6cm第19题图三、解答题(共36分) 20．(8分)如图所示，在四边形ABCD中，AB＝CD，M，N，P分别是AD，BC，BD的中点，∠ABD＝20°，∠BDC＝70°，求∠PMN的度数．解：∠PMN＝25° 21．(10分)如图，已知E为▱ABCD中DC边的延长线上的一点，且CE＝DC，连接AE，交BC于点F，连接AC交BD于点O，连接OF，试说明AB＝2OF.解：连接BE，∵四边形ABCD为平行四边形，∴AB∥CD，AB＝CD，AO＝OC，∵CE＝CD，∴AB∥CE，AB＝CE，∴四边形ABEC为平行四边形，∵BF＝FC，∴OF为△ABC的中位线，∴OF＝AB，即AB＝2OF 22．(10分)如图，△ABC中，中线BD，CE相交于O，F，G分别为OB，OC的中点．求证：四边形DEFG为平行四边形．【综合应用】解：证明：∵BD，CE分别是△ABC的中线，∴DE为△ABC的中位线，∴DEBC，又∵F，G分别为OB，OC的中点，∴FGBC，∴DEFG，∴四边形DEFG为平行四边形∥∥∥