八年级上数学课件八年级上册数学课件《三角形内角和定理》 北师大版 (5)_北师大版

八年级上数学课件八年级上册数学课件《三角形内角和定理》 北师大版 (5)_北师大版

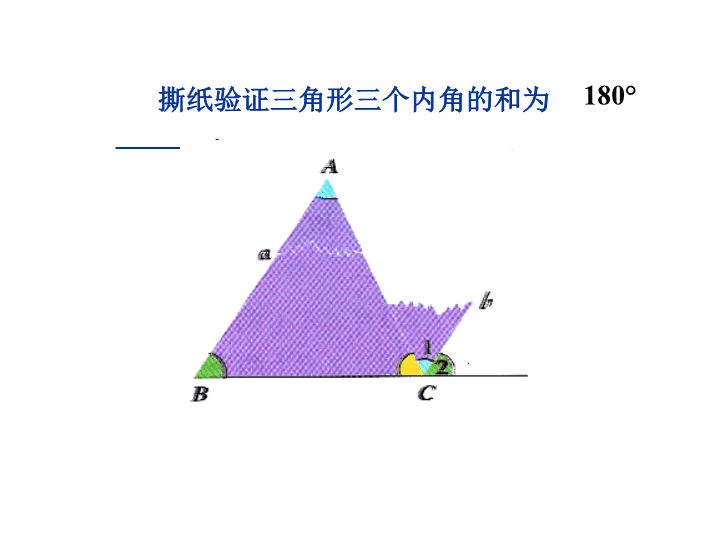
5.三角形内角和定理（第1课时）第七章平行线的证明 教学目标1、证明三角形内角和定理。2、探索证明过程，发展推理能力。3、在一题多解、一题多变中积累解决几何的经验，提升综合能力。 撕纸验证三角形三个内角的和为_______.180° 证明:三角形三个内角的和等于180°已知：如图,△ABC求证：∠A+∠B+∠C=180°BACED〖方法1〗证明：过A点作DE∥BC∵DE∥BC（已作）∴∠DAB=∠B，∠EAC=∠C（两直线平行，内错角相等）∵∠DAB+∠BAC+∠EAC=180°(1平角=180°)∴∠BAC+∠B+∠C=180°(等量代换) BAC〖方法2〗证明：作BC的延长线CD，过点C作射线CE∥BA。∵CE∥BA∴∠B=∠ECD（两直线平行，同位角相等）∠A=∠ACE（两直线平行，内错角相等）∵∠BCA+∠ACE+∠ECD=180°(1平角=180°)∴∠A+∠B+∠ACB=180°(等量代换)ED还有其他的证明方法吗？ 方法三如图，在BC边上任取一点D，过D作DE∥AB交AC于E，作DF∥AC交AB于F．∵DE∥AB，∴　∠1=∠B，∠2=∠4．（两直线平行，同位角相等）∵DF∥AC，∴　∠3=∠C，∠A=∠4（两直线平行，同位角相等）∴∠2=∠A(等量代换）又　∠1+∠2+∠3=180°，∴　∠A+∠B+∠C=180°． 方法四过点A作AD∥BC（如图）∵AD∥BC，∴　∠1=∠C，(两直线平行，内错角相等）∠DAB+∠ABC=180°（两直线平行，同旁内角互补）∴∠BAC+∠B+∠C=∠DAB+∠ABC=180° 方法五如图，过点A任作一条射线AD，再作BE∥AD，CF∥AD．∵BE∥AD∥CF，∴　∠1=∠3，∠2=∠4（两直线平行，内错角相等）∵∠EBC+∠BCF=180°（两直线平行，同旁内角相等）∴∠BAC+∠ABC+∠ACB=∠EBC+∠BCF=180°． 练习一1、△ABC中，∠C=90°，∠A=30°，∠B=.2、∠A=50°，∠B=∠C，则△ABC中∠B=.3、△ABC中可以有3个锐角吗？3个直角呢？2个直角呢？若有1个直角,另外两角有什么特点?4、三角形的三个内角中，只能有__个直角或__个钝角5、任意一个三角形，至少有__个锐角,至多有__个锐角6、三角形中三角之比为1∶2∶3，则三个角各为多少度？ 7、（p179随堂1）1、直角三角形的两锐角之和是度？证明你的结论。ABC已知：在△ABC中，∠C=90°.求证：∠A+∠B=90°90°证明：∵∠A+∠B+∠C=180°(三角形内角和定理）∴∠A+∠B=180°-∠C(等式基本性质）∵∠C=90°（已知）∴∠A+∠B=90°（等量代换） 例1、如图，在△ABC中，∠B=38°，∠C=62°，AD是△ABC的角平分线，求∠ADB的度数。ABDC解：在△ABC中，∵∠B+∠C+∠BAC=180°(三角形内角和定理）∴∠B=38°，∠C=62°（已知）∴∠BAC=180°-38°-62°=80°（等式的性质）∵AD平分∠BAC（已知）∴∠BAD=∠CAD=∠BAC=40°（角平分线的定义）在△ADB中，∠B+∠BAD+∠ADB=180°(三角形内角和定理）∵∠B=38°（已知），∠BAD=40°（已证）∴∠ADB=180°-38°-40°=102°(等式的性质） 练习2课本p179随堂33、已知：如图，在△ABC中，∠A=60°，∠C=70°，点D，E分别在AB和AC上，且DE∥BC。求证：∠ADE=50°ABCDE 已知：△ABC中，∠C=∠B=2∠A(a)求∠B的度数(b)若BD是AC边上的高，求∠DBC的度数.练习2CBAD 今天的收获证明三角形内角和定理的几种方法三角形内角和定理的简单应用辅助线的作法技巧 达标测评练习册P88