人教版七年级数学下册期考重难点突破、典例剖析与精选练习：解一元一次不等式组（附答案与全解全析）

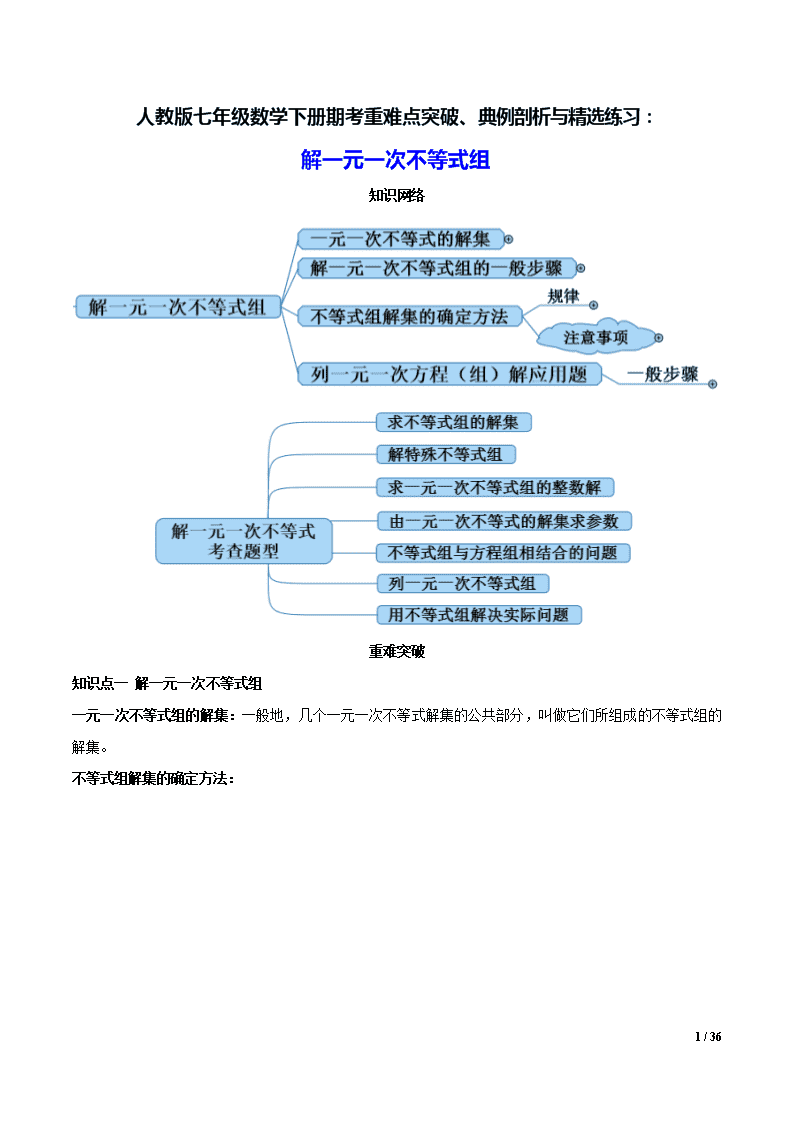
人教版七年级数学下册期考重难点突破、典例剖析与精选练习：解一元一次不等式组（附答案与全解全析）

人教版七年级数学下册期考重难点突破、典例剖析与精选练习：‎ 解一元一次不等式组 知识网络 重难突破 知识点一 解一元一次不等式组 一元一次不等式组的解集：一般地，几个一元一次不等式解集的公共部分，叫做它们所组成的不等式组的解集。‎ 不等式组解集的确定方法：‎ ‎ 36 / 36‎ ‎【注意】‎ ‎1.在求不等式组的解集的过程中，通常是利用数轴来确定不等式组的解集。‎ ‎2.利用数轴表示不等式组解集时，要把几个不等式的解集都表示出来，不能仅画公共部分。‎ 解一元一次不等式组的一般步骤：‎ ‎1.求出不等式组中各不等式的解集 ‎2.将各不等式的解决在数轴上表示出来。‎ ‎3.在数轴上找出各不等式解集的公共部分，这个公共部分就是不等式组的解集。‎ ‎【考查题型汇总】‎ 考查题型一 求不等式组的解集 典例1（2019·洛阳市期中）已知关于x的不等式3x﹣m+1＞0的最小整数解为2，则实数m的取值范围是（　　）‎ A．4≤m＜7 B．4＜m＜7 C．4≤m≤7 D．4＜m≤7‎ 变式1-1（2020·和平县期中）不等式组的解集在数轴上表示正确的是（　　）‎ A． B．‎ C． D．‎ 变式1-2（2020·沈阳市期中）下列四个不等式组中，解集在数轴上表示如图所示的是（　　）‎ ‎ 36 / 36‎ A． B． C． D．‎ 变式1-3（2019·南通市期中）已知点P（1﹣a，2a+6）在第四象限，则a的取值范围是（　　）‎ A．a＜﹣3 B．﹣3＜a＜1 C．a＞﹣3 D．a＞1‎ 变式1-4（2019长沙市期中）已知三个非负数a、b、c满足若，则的最小值为（ ）‎ A． B． C． D．－1‎ 考查题型二 解特殊不等式组 典例2（2019·遂宁市期末）已知0≤a–b≤1且1≤a+b≤4，则a的取值范围是( )‎ A．1≤a≤2 B．2≤a≤3 C．≤a≤ D．≤a≤‎ 变式2-1（2018·许昌市期末）若关于x的不等式组式的整数解为x=1和x=2，则满足这个不等式组的整数a，b组成的有序数对（a，b）共有（ ）对 A．0 B．1 C．3 D．2‎ 变式2-2（2019·北京市期中）三角形的三个内角分别为x,y,z，且，，则y的取值范围是__________‎ 考查题型三 求一元一次不等式组的整数解 典例3（2018·泉州市期中）若关于x的不等式的整数解共有4个，则m的取值范围是（　　）‎ A．6＜m＜7 B．6≤m＜7 C．6≤m≤7 D．6＜m≤7‎ 变式3-1（2019·泉州市期中）不等式组的最小整数解是（ ）‎ A．-1 B．0 C．1 D．2‎ 变式3-2（2019·温州市期中）已知4＜m＜5，则关于x的不等式组的整数解共有（　　）‎ A．1个 B．2个 C．3个 D．4个 变式3-3（2019·崇左市期中）不等式＋1<的负整数解有(　　)‎ A．1个 B．2个 C．3个 D．4个 ‎ 36 / 36‎ 考查题型四 由一元一次不等式的解集求参数 典例4（2019·苏州市期末）关于的不等式组无解，那么的取值范围为（ ）‎ A． B． C． D．‎ 变式4-1（2020·洛阳市期中）关于x的不等式组的解集为x＜3，那么m的取值范围为（ ）‎ A．m=3 B．m＞3 C．m＜3 D．m≥3‎ 变式4-2（2019·安陆市期末）若不等式组无解，则的取值范围为（ ）‎ A． B． C． D．‎ 变式4-3（2019·石家庄市期末）不等式组的解集是x＞1，则m的取值范围是（　　）‎ A．m≥1 B．m≤1 C．m≥0 D．m≤0‎ 考查题型五 不等式组与方程组相结合的问题 典例5（2019·南阳市期末）在关于x、y的方程组中，未知数满足x≥0，y＞0，那么m的取值范围在数轴上应表示为(　　)‎ A． B．‎ C． D．‎ 变式5-1（2019·洛阳市期中）已知方程组的解满足，则( ).‎ A．>-1 B．>1 C．<-l D．<1‎ 变式5-2（2019·安岳县期中）已知实数x，y，m满足，且y为负数，则m的取值范围是（ ）‎ A．m＞6 B．m＜6 C．m＞﹣6 D．m＜﹣6‎ 变式5-3（2019·合肥县期中）关于，的方程组的解满足，则 ‎ 36 / 36‎ 的取值范围是（ ）‎ A． B． C． D．‎ 变式5-4（2018·合肥市期中）若关于 的二元一次方程组 的解满足 ,则 的取值范围是( )．‎ A． B． C． D．‎ 变式5-5（2018·重庆市期末）关于的方程的解为正数，且关于的不等式组有解，则符合题意的整数有（　　）个．‎ A．4 B．5 C．6 D．7‎ 知识点二 列一元一次不等式（组）解应用题 列一元一次不等式（组）解应用题的一般步骤：‎ ‎（1）审：认真审题，分清已知量、未知量及其关系，找出题中不等关系，要抓住题设中的关键“字眼”，如“大于”“小于”“不小于”“不大于”“至少”“最多”等.‎ ‎（2）设：设出适当的未知数,并用含未知数的代数式表示出题目中涉及的量.‎ ‎（3）列：根据题中的不等关系，列出不等式.‎ ‎（4）解：解出所列不等式的解集.‎ ‎（5）验：检验答案是否符合题意.‎ ‎（6）答：写出答案.‎ 在以上步骤中，审题是基础，根据题意找出不等关系是关键，而根据不等关系列出不等式又是解题难点.以上过程可简单表述为: .‎ ‎【考查题型汇总】‎ 考查题型六 列一元一次不等式组 典例6（2019·安陆市期末）如果点P（2x＋6，x－4）在平面直角坐标系的第四象限内，那么x的取值范围在数轴上可表示为（ ）‎ A． B． ‎ C． D．‎ 变式6-1（2019·青岛市期末）如图，天平右盘中的每个砝码的质量都是，则物体的质量 ‎ 36 / 36‎ 的取值范围，在数轴上可表示为（ ）‎ A． B．‎ C． D．‎ 变式6-2（2019·成都市期中）若干个苹果分给x个小孩，如果每人分3个，那么余7个；如果每人分5个，那么最后一人分到的苹果不足5个，则x满足的不等式组为（　　）‎ A．0＜（3x+7）﹣5（x﹣1）≤5 B．0＜（3x+7）﹣5（x﹣1）＜5‎ C．0≤（3x+7）﹣5（x﹣1）＜5 D．0≤（3x+7）﹣5（x﹣1）≤5‎ 变式6-3（2018·深圳市期末）如果点P(x-4，x+3)在平面直角坐标系的第二象限内，那么x的取值范围在数轴上可表示为( )‎ A． B．‎ C． D．‎ 变式6-4（2020·深圳市期末）如图，按下面的程序进行运算.规定：程序运行到“判断结果是否大于”为一次运算.若运算进行了次停止，则的取值范围是（ ）‎ A． B． C． D．‎ 考查题型七 用不等式组解决实际问题 典例7（2019·石家庄市期末）“绿水青山就是金山银山”，为保护生态环境，A，B两村准备各自清理所属区域养鱼网箱和捕鱼网箱，每村参加清理人数及总开支如下表：‎ ‎ 36 / 36‎ 村庄 清理养鱼网箱人数/人 清理捕鱼网箱人数/人 总支出/元 A ‎15‎ ‎9‎ ‎57000‎ B ‎10‎ ‎16‎ ‎68000‎ ‎（1）若两村清理同类渔具的人均支出费用一样，求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元；‎ ‎（2）在人均支出费用不变的情况下，为节约开支，两村准备抽调40人共同清理养鱼网箱和捕鱼网箱，要使总支出不超过102000元，且清理养鱼网箱人数小于清理捕鱼网箱人数，则有哪几种分配清理人员方案？‎ 变式7-1（2020·渠县期末）在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元.‎ ‎（1）求每台电脑、每台电子白板各多少万元?‎ ‎（2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低.‎ 变式7-2（2019·长沙市期中）今年义乌市准备争创全国卫生城市，某小区积极响应，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买2个温馨提示牌和3个垃圾箱共需550元，且垃圾箱的单价是温馨提示牌单价的3倍．‎ ‎（1）求温馨提示牌和垃圾箱的单价各是多少元？‎ ‎（2）该小区至少需要安放48个垃圾箱，如果购买温馨提示牌和垃圾箱共100个，且费用不超过10000元，请你列举出所有购买方案，并指出哪种方案所需资金最少？最少是多少元？‎ 变式7-3（2019·佛山市期中）快递公司为提高快递分拣的速度，决定购买机器人来代替人工分拣．已知购买甲型机器人1台，乙型机器人2台，共需14万元；购买甲型机器人2台，乙型机器人3台，共需24万元．‎ ‎（1）求甲、乙两种型号的机器人每台的价格各是多少万元；‎ ‎（2）已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件，该公司计划购买这两种型号的机器人共8台，总费用不超过41万元，并且使这8台机器人每小时分拣快递件数总和不少于8300件，则该公司有哪几种购买方案？哪个方案费用最低，最低费用是多少万元？‎ ‎ 36 / 36‎ 巩固训练 一、 选择题（共10小题）‎ ‎1．（2019·盐城市期末）关于x的不等式组的解集为x＞1，则a的取值范围是（　　）‎ A．a≥1 B．a＞1 C．a≤1 D．a＜1‎ ‎2．（2020·德州市期中）已知点M（1﹣2m，m﹣1）关于x轴的对称点在第一象限，则m的取值范围在数轴上表示正确的是（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎3．（2019·泰安市期末）若关于x的一元一次不等式组无解，则a的取值范围是（　　）‎ A．a≥6 B．a＞6 C．a≤﹣6 D．a＜﹣6‎ ‎4．（2019·邯郸市期末）不等式组的整数解的个数是(　　)‎ A．1个 B．2个 C．3个 D．4个 ‎5．（2018·天水市期末）如果关于x的一元一次不等式组的解集在数轴上的表示如图所示，那么该不等式组的解集为（ ）‎ A．x≥﹣1 B．x＜2 C．﹣1≤x≤2 D．﹣1≤x＜2‎ ‎6．（2018·静宁县期末）若不等式组3＜x≤a的整数解恰有4个，则a的取值范围是（　 ）‎ A．a＞7 B．7＜a＜8 C．7≤a＜8 D．7＜a≤8‎ ‎ 36 / 36‎ ‎7．（2018·长沙市期末）不等式组的解集是(　　)‎ A．1＜x＜3 B．x＞3 C．x＞1 D．x＜1‎ ‎8．（2018·大连市期末）把不等式组的解集表示在数轴上，正确的是（ ）‎ A． B．‎ C． D．‎ ‎9．（2017·无锡市期中）晓明家到学校的路程是3 500米，晓明每天早上7∶30离家步行去上学，在8∶10（含8∶10）至8∶20（含8∶20）之间到达学校。如果设晓明步行的速度为x米/分，则晓明步行的速度范围是（　 　）‎ A．70≤x≤87.5 B．x≤70或x≥87.5 C．x≤70 D．. x≥87.5‎ ‎10．（2018·池州市期中）某学校组织员工去公园划船，报名人数不足50人，在安排乘船时发现，每只船坐6人，剩下18人无船可乘；每只船坐10人，那么其余的船坐满后，有一只船不空也不满，参加划船的员工共有（　　）‎ A．48人 B．45人 C．44人 D．42人 一、 填空题（共5小题）‎ ‎11．（2018·长沙市期末）已知不等式组的解集是2＜x＜3，则a+b的值是_____．‎ ‎12．（2019·北京市期中）在平面直角坐标系中，点(-7+m,2m+1) 在第三象限，则m的取值范围是_________.‎ ‎13．（2019·邯郸市期末）如果关于的不等式组的解集是，则的取值范围是_____________‎ ‎14．（2019·长春市期中）不等式组 的正整数的解的和是________________．‎ ‎15．（2019·济南市期末）不等式组的解集为__________．‎ ‎ 36 / 36‎ 一、 解答题（共2小题）‎ ‎16．（2020·贵港市期末）解不等式组：并将解集在数轴上表示．‎ ‎17．（2019·济南市期末）某校九年级举行数学竞赛，学校准备购买甲、乙、丙三种笔记本奖励给获奖学生，已知甲种笔记本单价比乙种笔记本单价高10元，丙种笔记本单价是甲种笔记本单价的一半，单价和为80元． ‎ ‎（1）甲、乙、丙三种笔记本的单价分别是多少元？ ‎ ‎（2）学校计划拿出不超过950元的资金购买三种笔记本40本，要求购买丙种笔记本20本，甲种笔记本超过5本，有哪几种购买方案？‎ ‎ 36 / 36‎ 人教版七年级数学下册期考重难点突破、典例剖析与精选练习：‎ 解一元一次不等式组 知识网络 重难突破 知识点一 解一元一次不等式组 一元一次不等式组的解集：一般地，几个一元一次不等式解集的公共部分，叫做它们所组成的不等式组的解集。‎ 不等式组解集的确定方法：‎ ‎ 36 / 36‎ ‎【注意】‎ ‎1.在求不等式组的解集的过程中，通常是利用数轴来确定不等式组的解集。‎ ‎2.利用数轴表示不等式组解集时，要把几个不等式的解集都表示出来，不能仅画公共部分。‎ 解一元一次不等式组的一般步骤：‎ ‎1.求出不等式组中各不等式的解集 ‎2.将各不等式的解决在数轴上表示出来。‎ ‎3.在数轴上找出各不等式解集的公共部分，这个公共部分就是不等式组的解集。‎ ‎【考查题型汇总】‎ 考查题型一 求不等式组的解集 典例1（2019·洛阳市期中）已知关于x的不等式3x﹣m+1＞0的最小整数解为2，则实数m的取值范围是（　　）‎ A．4≤m＜7 B．4＜m＜7 C．4≤m≤7 D．4＜m≤7‎ ‎【答案】A ‎【详解】‎ 解:解不等式3x﹣m+1＞0，得：x＞，‎ ‎∵不等式有最小整数解2，‎ ‎∴1≤＜2，‎ 解得：4≤m＜7，‎ 故选A．‎ ‎ 36 / 36‎ 变式1-1（2020·和平县期中）不等式组的解集在数轴上表示正确的是（　　）‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】‎ 解不等式x+2＞0，得：x＞-2，‎ 解不等式2x-4≤0，得：x≤2，‎ 则不等式组的解集为-2＜x≤2，‎ 将解集表示在数轴上如下：‎ 故选C．‎ 变式1-2（2020·沈阳市期中）下列四个不等式组中，解集在数轴上表示如图所示的是（　　）‎ A． B． C． D．‎ ‎【答案】D ‎【详解】‎ 由解集在数轴上的表示可知，该不等式组为，‎ 故选D．‎ 变式1-3（2019·南通市期中）已知点P（1﹣a，2a+6）在第四象限，则a的取值范围是（　　）‎ A．a＜﹣3 B．﹣3＜a＜1 C．a＞﹣3 D．a＞1‎ ‎【答案】A ‎【详解】‎ 解：∵点P（1﹣a，2a+6）在第四象限，‎ ‎ 36 / 36‎ ‎∴‎ 解得a＜﹣3．‎ 故选A．‎ 变式1-4（2019长沙市期中）已知三个非负数a、b、c满足若，则的最小值为（ ）‎ A． B． C． D．－1‎ ‎【答案】B ‎【详解】‎ 解：联立，得.‎ 由题意知：a，b，c均是非负数，‎ 则，‎ 解得 ‎ m=3a+b−7c=3(−3+7c)+(7−11c)−7c=−2+3c，‎ 当 时,m有最小值,即 ‎ 当时,m有最大值,即 ‎ 故选B.‎ 考查题型二 解特殊不等式组 典例2（2019·遂宁市期末）已知0≤a–b≤1且1≤a+b≤4，则a的取值范围是( )‎ A．1≤a≤2 B．2≤a≤3 C．≤a≤ D．≤a≤‎ ‎【答案】C ‎【详解】‎ 解：0≤a－b≤1，①‎ ‎1≤a＋b≤4，②‎ ‎①＋②，得1≤2a≤5，‎ ‎ 36 / 36‎ 解得：≤a≤.‎ 故选C.‎ 变式2-1（2018·许昌市期末）若关于x的不等式组式的整数解为x=1和x=2，则满足这个不等式组的整数a，b组成的有序数对（a，b）共有（ ）对 A．0 B．1 C．3 D．2‎ ‎【答案】D ‎【详解】‎ 由①得： ‎ 由②得： ‎ 不等式组的解集为：‎ ‎∵整数解为为x=1和x=2‎ ‎∴， ‎ 解得：，‎ ‎∴a=1，b=6,5‎ ‎∴整数a、b组成的有序数对（a,b）共有2个 故选D 变式2-2（2019·北京市期中）三角形的三个内角分别为x,y,z，且，，则y的取值范围是__________‎ ‎【答案】36°≤y≤ ‎ ‎【解析】‎ ‎∵三角形的三个内角分别为x，y，z，‎ ‎∴x+y+z=180°，‎ ‎∵，，‎ ‎∴，‎ ‎ 36 / 36‎ ‎∴y最小=x，y最大=3x，‎ 当y最小=x时，有x+x+3x=180°，解得：x=36°，此时y最小=36°；‎ 当y最大=3x时，有x+3x+3x=180°，解得：x=，此时y最大=；‎ ‎∴y的取值范围是：.‎ 故答案为：.‎ 考查题型三 求一元一次不等式组的整数解 典例3（2018·泉州市期中）若关于x的不等式的整数解共有4个，则m的取值范围是（　　）‎ A．6＜m＜7 B．6≤m＜7 C．6≤m≤7 D．6＜m≤7‎ ‎【答案】D ‎【详解】‎ 解：‎ 由（1）得，x＜m，‎ 由（2）得，x≥3，‎ 故原不等式组的解集为：3≤x＜m，‎ ‎∵不等式的正整数解有4个，‎ ‎∴其整数解应为：3、4、5、6，‎ ‎∴m的取值范围是6＜m≤7．‎ 故选：D．‎ 变式3-1（2019·泉州市期中）不等式组的最小整数解是（ ）‎ A．-1 B．0 C．1 D．2‎ ‎【答案】B ‎【详解】，‎ ‎ 36 / 36‎ 解不等式①得，x≤2，‎ 解不等式②得，x>-1，‎ 所以不等式组的解集是：-12(x+1)，得：x>3，‎ ‎∵不等式组无解，‎ ‎∴m⩽3，‎ 故选：D 变式4-1（2020·洛阳市期中）关于x的不等式组的解集为x＜3，那么m的取值范围为（ ）‎ A．m=3 B．m＞3 C．m＜3 D．m≥3‎ ‎【答案】D ‎【详解】‎ 解不等式组得：，‎ ‎∵不等式组的解集为x＜3‎ ‎∴m的范围为m≥3，‎ 故选D．‎ 变式4-2（2019·安陆市期末）若不等式组无解，则的取值范围为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【详解】‎ 解不等式，得：x＞8，‎ ‎∵不等式组无解，‎ ‎∴4m≤8，‎ 解得m≤2，‎ 故选A．‎ ‎ 36 / 36‎ 变式4-3（2019·石家庄市期末）不等式组的解集是x＞1，则m的取值范围是（　　）‎ A．m≥1 B．m≤1 C．m≥0 D．m≤0‎ ‎【答案】D ‎【详解】‎ 解：不等式整理得：，由不等式组的解集为x＞1，得到m+1≤1，解得：m≤0.‎ 故选D.‎ 考查题型五 不等式组与方程组相结合的问题 典例5（2019·南阳市期末）在关于x、y的方程组中，未知数满足x≥0，y＞0，那么m的取值范围在数轴上应表示为(　　)‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】‎ ‎，解方程组得：，‎ ‎∵x≥0，y＞0，‎ ‎∴，‎ ‎∴－2≤m＜3.‎ 故选C.‎ 变式5-1（2019·洛阳市期中）已知方程组的解满足，则( ).‎ A．>-1 B．>1 C．<-l D．<1‎ ‎【答案】C ‎【详解】‎ ‎ 36 / 36‎ 把方程组的两式相加，得3x+3y=2+2m 两边同时除以3，得x+y=所以＜0即m＜-1．故选C 变式5-2（2019·安岳县期中）已知实数x，y，m满足，且y为负数，则m的取值范围是（ ）‎ A．m＞6 B．m＜6 C．m＞﹣6 D．m＜﹣6‎ ‎【答案】A ‎【解析】‎ 根据非负数的性质列出方程求出x、y的值，然后根据y是负数即可得到一个关于m的不等式，从而求得m的范围：‎ 根据算术平方根和绝对值的非负数性质，得：，解得：．‎ ‎∵y为负数，∴6﹣m＜0，解得：m＞6．‎ 故选A．‎ 变式5-3（2019·合肥县期中）关于，的方程组的解满足，则的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【详解】‎ ‎①-②，得2x+3y=3m+6‎ ‎∵2x+3y>7‎ ‎∴3m+6>7‎ ‎∴m>‎ 变式5-4（2018·合肥市期中）若关于 的二元一次方程组 的解满足 ,则 ‎ ‎ 36 / 36‎ 的取值范围是( )．‎ A． B． C． D．‎ ‎【答案】B ‎【详解】‎ 两式相加得，‎ ‎，‎ ‎∵ x+y<505，‎ ‎∴，‎ 解得．‎ 故选：.‎ 变式5-5（2018·重庆市期末）关于的方程的解为正数，且关于的不等式组有解，则符合题意的整数有（　　）个．‎ A．4 B．5 C．6 D．7‎ ‎【答案】C ‎【详解】‎ ‎∵关于x的方程的解为正数,  ∴2-(x+m)=2(x-2), ‎ 解得:x= , ‎ 则6-m>0, ‎ 故m<6,  ∵关于y的不等式组 有解,  ∴m+2≤y≤3m+4,  且m+2≤3m+4,  解得:m≥-1,  故m的取值范围是:-1≤m<6,  ‎ ‎ 36 / 36‎ ‎∵x-2≠0,  ∴x≠2,  ∴ ,  m≠0,  则符合题意的整数m有:-1,1,2,3,4,5,共6个.  故选C..‎ 知识点二 列一元一次不等式（组）解应用题 列一元一次不等式（组）解应用题的一般步骤：‎ ‎（1）审：认真审题，分清已知量、未知量及其关系，找出题中不等关系，要抓住题设中的关键“字眼”，如“大于”“小于”“不小于”“不大于”“至少”“最多”等.‎ ‎（2）设：设出适当的未知数,并用含未知数的代数式表示出题目中涉及的量.‎ ‎（3）列：根据题中的不等关系，列出不等式.‎ ‎（4）解：解出所列不等式的解集.‎ ‎（5）验：检验答案是否符合题意.‎ ‎（6）答：写出答案.‎ 在以上步骤中，审题是基础，根据题意找出不等关系是关键，而根据不等关系列出不等式又是解题难点.以上过程可简单表述为: .‎ ‎【考查题型汇总】‎ 考查题型六 列一元一次不等式组 典例6（2019·安陆市期末）如果点P（2x＋6，x－4）在平面直角坐标系的第四象限内，那么x的取值范围在数轴上可表示为（ ）‎ A． B． ‎ C． D．‎ ‎【答案】C ‎【详解】‎ 由点P（2x＋6，x－4）在平面直角坐标系的第四象限内，得．‎ 解一元一次不等式组，先求出不等式组中每一个不等式的解集，再利用口诀求出这些解集的公共部分：同大取大，同小取小，大小小大中间找，大大小小解不了（无解）．因此，‎ ‎ 36 / 36‎ ‎．‎ 变式6-1（2019·青岛市期末）如图，天平右盘中的每个砝码的质量都是，则物体的质量的取值范围，在数轴上可表示为（ ）‎ A． B．‎ C． D．‎ ‎【答案】A ‎【解析】‎ ‎∵由图可知，1g2,‎ 由②得：x<6,‎ 所以不等式组的解集为2

查看更多