- 2021-10-26 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
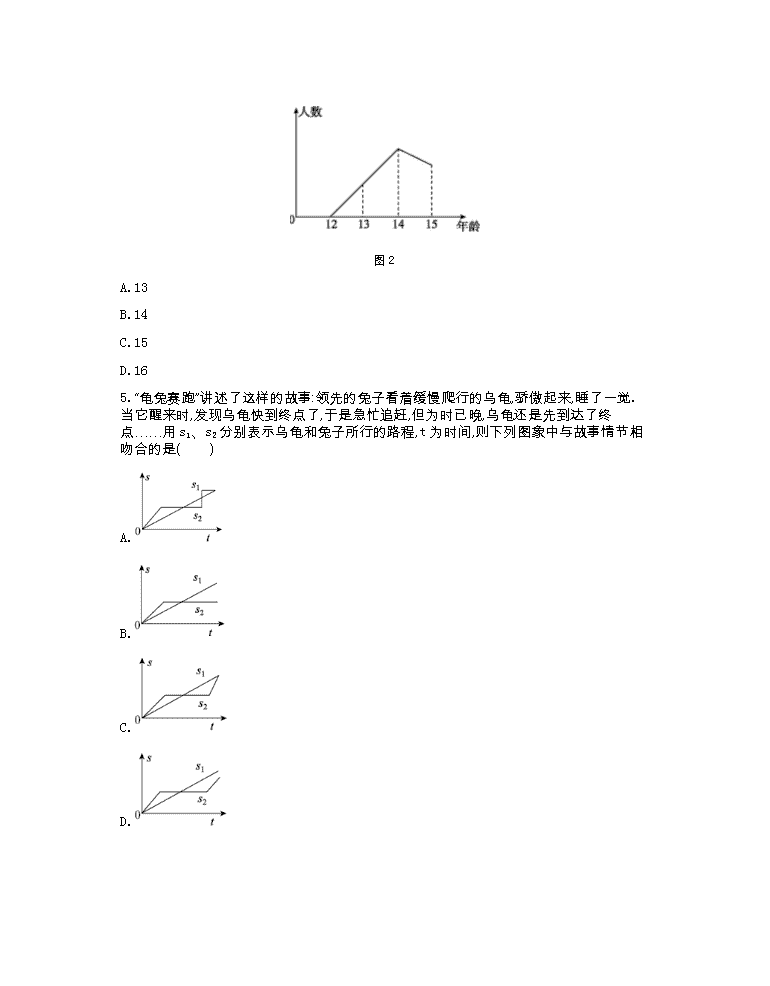
北师大版七年级数学(下册)第三章测试卷(附参考答案)
数学七下北师测试卷第三章 1.在利用太阳能热水器烧热水的过程中,热水器里的水温会随着太阳照射时间的长短而变化,这个问题中因变量是( ) A.水的温度 B.太阳光强弱 C.太阳照射时间 D.热水器的容积 2.如图1,图中是某市某天的温度随时间的变化图象,通过观察可知下面说法错误的是( ) 图1 A.这天16点左右温度最高 B.这天3点左右温度最低 C.这天最高温度与最低温度的差是13℃ D.这天21点时温度是30℃ 3.某小区每月水费的收费标准如下表,下列说法不正确的是( ) 用水量x/吨 1 2 3 4 5 水费y/元 3.5 5 6.5 8 9.5 A.水费随着用水量的增加而增加 B.水费y与用水量x之间的关系为y=2+1.5x C.如果用水10吨,那么应缴15元的水费 D.如果缴了20元水费,则这个月用了12吨水 4.阳光中学毕业班学生年龄特征如图2所示,则 周岁的学生居多.( ) 图2 A.13 B.14 C.15 D.16 5.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点……用s1、s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是( ) A. B. C. D. 6.变量y随x的变化而变化,可用关系式表示为y=3x+5,下列说法:①x是自变量,y是因变量;②y是变量,它的值与x无关;③用关系式表示的不能用图象表示;④y与x的关系还可以用表格和图象表示.其中说法正确的是( ) A.①② B.②③ C.①③ D.①④ 7.小颖的父亲饭后出去散步,从家走20分钟到一个离家900米的报亭,看了10分钟报纸后,用15分钟返回家里,用下图中哪幅图能较好刻画小颖父亲离家的时间与距离间的关系( ) A. B. C. D. 8.地壳的厚度约为8~40km,在地表以下不太深的地方,温度可以按y=3.5x+t计算,其中x是深度,t是地球表面的温度,y是所达深度的温度.当t=5℃,深度为20km时的温度是( ) A.70℃ B.75℃ C.80℃ D.无法确定 9.一天,小军和爸爸去登山,已知山脚到山顶的路程为300米,小军先走了一段路程,爸爸才开始出发,图3中两条线段分别表示小军和爸爸离开山脚登山的路程s(米)与登山所用的时间t(分钟)的关系(从爸爸开始登山时计时),根据图象,下列说法错误的是( ) 图3 A.爸爸开始登山时,小军已走了50米 B.爸爸走了5分钟,小军仍在爸爸的前面 C.小军比爸爸晚到山顶 D.爸爸前10分钟登山的速度比小军慢,10分钟后登山的速度比小军快 10.经测量,人运动时心跳速率通常和人的年龄有关.如果用x表示一个人的年龄,用y示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么y=0.8(220-x),根据此关系式计算一个18岁的青少年所能承受的每分钟的最高心跳次数是(取整数)( ) A.80 B.100 C.162 D.161 11.水箱储水20立方米,每小时流量为0.5立方米,随着流水时间的变化,水箱的存水量也随之变化;在这个变化过程中,自变量是 ,因变量是 .若流水时间为t(小时),存水量为Q(立方米)与t的关系式为 . 12.在大气层中,每升高1米,温度降低0.006℃,如果地面的温度为28℃,则离开地面h(米)的高空气温T(℃)可以表示为 . 13.定甲、乙两人在一次赛跑中,路程s与时间t的关系如图4所示,那么可以知道这是一次 米赛跑.甲、乙两人中先到达终点的是 ,乙在这次赛跑中的速度约为 米/秒.(取整数) 图4 14.某出租车公司规定:出租车收费与行驶路程之间的关系如图5所示,如果小燕乘出租车去学校花去了22元,那么小燕到学校走了 千米的路程. 图5 15.1~6个月的婴儿生长发育得非常快,他们的体重y(克)和月龄x(月)间的关系可以用y=a+700x,其中a是婴儿出生时体重.一个婴儿出生时的体重均为4000克,用表格表示如下,在1~6个月内,这个婴儿的体重y与x之间的关系为 . 月龄/月 1 2 3 4 5 6 体重/月 4700 5400 6100 6800 7500 8200 16.洲际弹道导弹的速度会随着时间的变化而变化,某种型号的洲际弹道导弹的速度v(千米/时)与时间t(小时)的关系是:v=1000+50t,现导弹发出小时即将击中目标,此时该导弹的速度为 . 17.如图6①所示,在长方形ABCD中,动点P从B出发,沿BC,CD,DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的图象如图6②所示,则△ABC的面积是 . 图6 18.某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置: 排数 1 2 3 4 … 座位数 50 53 56 59 … 上述问题中,第5排有 个座位,第6排有 个座位,第n排有 个座位. 19.A,B两地相距100米,甲、乙两人同时进行跑步练习,他们离A地的距离s(米)与时间t(秒)的关系如图7所示,仔细观察图象后填空: 图7 甲从 地出发,乙从 地出发,他们 向而行.甲的速度为 米/秒,乙的速度为 米/秒.甲、乙相遇时距离A地大约多少米? 20.某天放学后,小李步行回家,如图8所示,反映了他行走的速度与时间的变化关系. 图8 (1)请你根据图象填写下表: 时间/分钟 0 2 4 8 10 12 14 16 18 20 24 速度(千米/时) (2)根据图象或表格你能叙述一下小李行走的情况吗? 21.如图9,它表示甲、乙两人从同一个地点出发后的情况,到十点时,甲大约走了13千米,根据图象回答: (1)甲是几点钟出发? (2)乙是几点钟出发,到十点时,他大约走了多少千米? (3)到十点为止,哪个人的速度快? (4)两人最终在几点钟相遇? 图9 22.为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段达到节约用水的目的.某市规定用水收费标准如下:每户每月的用水不超过6立方米时, 水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费.该市某户今年3、4月份的用水量和水费如下表所示: 月份 用水量/立方米 水费/元 3 5 7.5 4 9 27 设某户月用水量为x(立方米),应交水费为y(元). (1)求a,c的值,并写出用水不超过6立方米和超过6立方米时,y与x之间的关系式; (2)若该户5月份的用水量为8立方米,求该户5月份的水费是多少元? 参考答案 1.A 2.C 3.C 4.B 5.D 6.D 7.D 8.B 9.D 10.D 11.时间存水量Q=20-0.5t 12.T=28-0.006h 13.100 甲 8 14.13 15.y=4000+700x 16.1025千米/时 17.10 18.62 65 47+3n 19.A 10 12.5 解:设相遇时距离A地x米,则,x≈44(米). 20.(1) 时间/分钟 0 2 4 8 10 12 14 16 18 20 24 速度(千米/时) 0 2.5 5 5 5 5 2.5 2.5 2.5 2.5 0 (2)解:由图象知小李放学后开始加速走,等速度达到5千米/时的时候开始匀速行走,大约过了8分钟,开始减速,直至速度为2.5千米/时,又开始匀速行走,大约过了6分钟又开始减速,4分钟后停止. 21.解:根据图象可知:(1)甲8点出发; (2)乙9点出发,到10时他大约走了13千米; (3)到10时为止,乙的速度快; (4)两人最终在12时相遇; 22.解:(1)当x≤6时,y=ax;当x>6时,y=6a+c(x-6). 当x=5时,y=7.5,所以5a=7.5,所以a=1.5; 当x=9时,y=27,所以6a+3c=27,所以c=6, 所以y=1.5x(x≤6),y=9+6(x-6)=6x-27(x>6). (2)因为x=8>6,所以y=6×8-27=21(元),所以5月份应交水费21元.查看更多