七年级下数学课件：7-1-2 平面直角坐标系 （共18张PPT)_人教新课标

七年级下数学课件：7-1-2 平面直角坐标系 （共18张PPT)_人教新课标

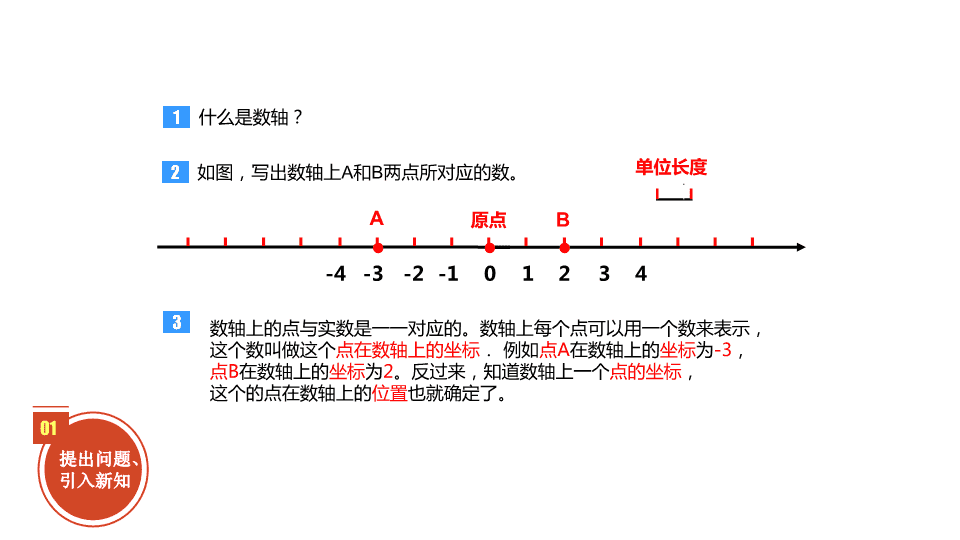
1 7.1.2 平面直角坐标系 01 提出问题、 引入新知 教学设计的第一环节 什么是数轴？1 如图，写出数轴上A和B两点所对应的数。2 0 1 2 3 4-1-2-3-4 A B原点 单位长度 3 数轴上的点与实数是一一对应的。数轴上每个点可以用一个数来表示， 这个数叫做这个点在数轴上的坐标． 例如点A在数轴上的坐标为-3， 点B在数轴上的坐标为2。反过来，知道数轴上一个点的坐标， 这个的点在数轴上的位置也就确定了。 类似于利用数轴确定直线上点的位置， 能不能找到一种办法来确定平面内的 点的位置呢？ B C A 如图，你如何确定平面上A、B、C各点的位置？ 教学设计的第二环节 02 探索新知、 解决问题 什么是平面直角坐标系？1 在平面直角坐标系中，什么是横轴、纵轴、原点？2 在坐标平面内如何求一个点的坐标？3 笛卡尔 ，法国著名的数学家。1596年出生于法国，早 在1637年以前，法国数学家、解析几何的创始人笛卡尔 受到了经纬度的启发在1637年以前笛卡尔受到了经纬度 的启发，地理上的经纬度是以赤道和本初子午线为标准 的，这两条线从局部上可以看成是平面内互相垂直的两 条直线。所以笛卡尔的方法是在平面内画两条互相垂直 的数轴，其中水平的数轴叫x轴(或横轴)，取向右为正方 向，铅直的数轴叫y轴(或纵轴)，取向上为正方向，它们 的交点是原点，这个平面叫坐标平面。探索：那么有了 坐标平面，大家想一想你能找到一种方法来确定A、B、 C各点的位置吗？ 简 介 教学设计的第三环节 03 形成概念、 发现特征 分析：类似于笛卡儿的方法， 这时我们可以在平面内画两条互相 垂直、原点重合的数轴，组成平面 直角坐标系。水平的数轴称为x 轴 或横轴，习惯上取向 右为正方向； 竖直的数轴称为 y 轴或 纵 轴，取 向上方向为正方向；两坐标轴的交 点为平面直角坐标系的原点。 x轴或横轴 y轴或纵轴 原点 l 互相垂直 l 原点重合 l 单位长度一般取相同的 两条数轴：（一般性特征） （1）互相垂直 （2）原点重合 （3）通常取向右、向上为正方向 （4）单位长度一般取相同的 请你在本子上画一平面直角坐标系。并说一说：平面直角坐标系具有哪些特征 呢？ O x y -3 -2 -1 1 2 3 4 3 2 1 -1 -2 -3 -4 XO 选择：下面四个图形中，是平面直角坐标系的是（ ） -3 -2 -1 1 2 3 3 2 1 -1 -2 -3 Y X X Y （A） 3 2 1 -1 -2 -3 X Y （B） 2 1 -1 -2O -3 -2 -1 1 2 3 3 2 1 -1 -2 -3 （C） O -3 -2 -1 1 2 3 3 2 1 -1 -2 -3 Y （D） O 3 1 4 2 5 -2 -1 -3 0 1 2 3 4 5-4 -3 -2 -1 x 横轴 y纵轴 有了平面直角坐标系，平面内的点就可以用一个有序数对来表示了，例如思考中的A、B、C三点就可以表示了。 ·A N M 有序数对(-2，3)就叫做A的坐标 记作：A（-2，3） （-2，3） B ( 3，2)· C ( 0，0) A的横坐标为-2 A的纵坐标为3 教学设计的第四环节 如何确定点Ｐ的坐标呢？ 04 合作探究、 形成技能 x y o - 1 1- 1 1 a b •　Ｐ（a,b） 横坐标 纵坐标 过点p作x、 y 轴 的 垂 线 横坐标在前， 纵坐标在后， 中间隔开用 逗号，勿忘 加括号！ 1 教学设计的第四环节 04 合作探究、 形成技能 已知Ｑ点的坐标为（m，n），如何确定点Ｑ的位置呢？2 y o - 1 1- 1 1 m n •　Ｑ x 步骤： ① 过x轴上表示m的点作x轴的垂线； ② 过y轴上表示n的点作y轴的垂线； ③ 两线的交点即为点Ｑ。 教学设计的第五环节 05 巩固训练、 熟练技能 写出图中A、B、C、D、E各点的坐标。例1 ( 2，3 ) ( 3，2 )( -2，1 ) ( -4，- 3 ) ( 1，- 2 ) 坐标是有序 数对。 教学设计的第五环节 05 巩固训练、 熟练技能 在平面内描出下列各点，并用线段把他们连接起来。A(-3,0)、B(-2,1)、C（0,-4）、 D(2,1)、E(3,0) 。（给学生发带坐标轴的格子纸，要求同学完成，随后与同组相比较。） 例2 y A B C D E 坐标平面上的点 一对有序实数 教学设计的第六环节 06 拓展练习、 开阔视野 ① (0 , 6), (-4, 3), (4 , 3) ② (-2 , 3), (-2 , -3), (2 , -3), (2 , 3) 解答题例3 在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来. 1 2 3 4 5 7 860-1-2-3-4-6 -5-7 -1 -6 -5 -4 -3 -2 1 2 3 4 5 6 7 8 9 · · ·· · · · P(0 , 6) A(-4,3) B(4,3) C(-2,3) D(2,3) E(-2,-3) F(2,-3) x y 观察图形，你觉得它像什么？ 由例3我们知道，数轴上的点与实数是一一对 应的。即：对于坐标平面内任意一点M，都有 唯一的一对有序实数（x, y）和它对应；反过 来，对于任意一对有序实数（x, y），在坐标 平面内都有唯一的一点M和它对应。 教学设计的第七环节 07 归纳总结、 反思知识 通过本堂课的学习 我学会了… … 我感到困惑的是… … 我体会到… … 丰收园 教学设计的第八环节 作业布置 08 作业布置、 分层训练 必做题:课本69页3、7题1 实践题：记录一下明天一天中每个整点的温度，绘制一张气温图。2 研究性课题作业：如何确定空间中一个点的位置？3 4 上网查阅全球定位系统GPS相关科普知识。 板书设计 7.1.2平面直角坐标系 1 2 3 4 5 7 860-1-2-3-4-6 -5-7 -1 -6 -5 -4 -3 -2 1 2 3 4 5 6 7 8 9 一：重点讲解区 1.平面直角坐标系的概念。 2.平面直角坐标系内点的表示。 X y 二：例题 例1： 例2： 三：练习 解答题