- 2021-10-25 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级上数学课件1-2-4 绝对值 课件(19张PPT)_人教新课标
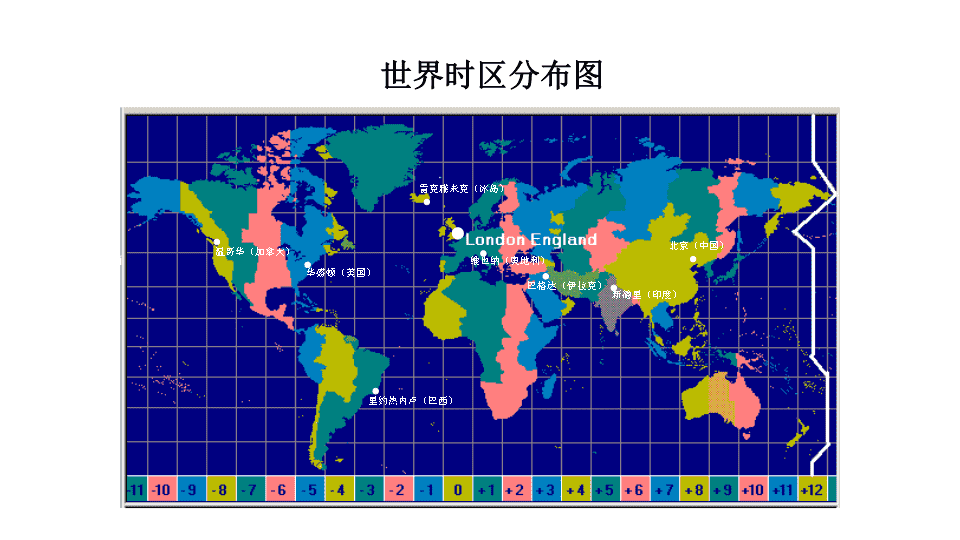
(Absolute Value) 世界时区分布图 雷克雅未克(冰岛) 维也纳(奥地利) 巴格达(伊拉克) 新德里(印度) 北京(中国) 华盛顿(美国) 温哥华(加拿大) 里约热内卢(巴西) 世界时区分布图 雷克雅未克(冰岛) 维也纳(奥地利) 巴格达(伊拉克) 新德里(印度) 北京(中国) 华盛顿(美国) 温哥华(加拿大) 里约热内卢(巴西) 时区数轴 雷克雅未克(冰岛) 维也纳(奥地利) 巴格达(伊拉克) 新德里(印度) 北京(中国) 华盛顿(美国) 温哥华(加拿大) 里约热内卢(巴西) 伦敦(英国) 什么是绝对值? 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10+11 +12-1-2-3-4-5-6-7-8-9-10-11 东 伦 敦 雷 克 雅 未 克 维 也 纳 巴 格 达 新 德 里 北 京 里 约 热 内 卢 华 盛 顿 温 哥 华 3个时区 3个时区 在数轴上一个数所对应的点与原点的距离叫做该数的绝对值(Absolute Value). 如: -3的绝对值等于3,记作 │ -3│=3. 想一想 互为相反数的两个数的绝对值有什么关系? 互为相反数的两 个数的绝对值相等。 例1:求下列各数的绝对值 9 4 -21, 0, , -7.8 解:|-21|=21 | 0 |=0 | |= |-7.8|=7.8 9 4 9 4 一个数的绝对值与这个数有什么关系? 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10+11 +12-1-2-3-4-5-6-7-8-9-10-11 东 伦 敦 雷 克 雅 未 克 维 也 纳 巴 格 达 新 德 里 北 京 里 约 热 内 卢 华 盛 顿 温 哥 华 正数的绝对值是它本身; 负数的绝对值是它的相反数; 0的绝对值是0. 正式足球比赛时所用足球的质量有严格的规定, 下表是6个足球的质量检测结果(用正数记超过规定 的克数,用负数记不足规定质量的克数). 第1个 第2个 第3个 第4个 第5个 第6个 -25 -10 +20 +30 +15 -40 请指出哪个足球质量最好,为什么? 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10+11 +12-1-2-3-4-5-6-7-8-9-10-11 数轴上两个点表示的数,右边的总比左边的大. 正数大于0; 负数小于0; 正数大于一切负数. 做一做 (1)在数轴上表示下列各数,并比较大小: -1.5, -3, -1, -4 由小到大排列:-4 < -3 < -1.5 < -1 -10 -5 5 x 0 1-1-1.5-3-4 (2)求出(1)中各数的绝对值,并比较 大小: 解:|-1.5|=1.5, |-3|=3, |-1|=1, |-4|=4 (3)联系(1)与(2),你发现负数如 何比较大小了吗? 两个负数比较大小时,绝 对值大的反而小! (1) -4 < -3 < -1.5 < -1 1 < 1.5 < 3 < 4 (2) 1 < 1.5 < 3 < 4 例2:比较下列每组数的大小: (1)-1和-5 (2) 和-2.76 5 方法一:利用数轴; -5 510-1 -5 510-2.7 6 5 例2 比较下列每组数的大小: (1) -1和-5; (2) - 和 -2.7 . 方法二: 6 5 解:(1) 因为│-1│=1, │-5│=5,1<5 所以 -1>-5 . (2) 因为│- │= , │-2.7│=2.7, <2.7 所以 - > -2.7 . 6 5 6 5 6 5 6 5 例3.如果有一个数的绝对值为3,那么这个 数是多少? 解:这个数可以是+3也可以是-3. 随堂练习 比较下列各组数的大小: (1) - ,- ; (2) │-7│,│ 7 │; (3) 0 ,│- │;(4) -0.5 ,- . 7 2 10 1 3 2 3 2 概念深化练习 下面的说法是否正确?请将错误的改过来. (1)有理数的绝对值一定比0大; (2)有理数的相反数一定比0小; (3)如果两个数的绝对值相等,那么这两个数相等; (4)互为相反数的两个数的绝对值相等. 试一试 1. 字母a表示一个数,-a表示什么?-a一定是负数吗? 2. 如果│a│=4,那么a等于多少? 3.(1)如果数a的绝对值等于a,那么a可能是正数吗? 可能是零吗?可能是负数吗? (2) 如果数a的绝对值大于a,那么a可能是正数吗? 可能是零吗?可能是负数吗? (3)一个数的绝对值可能小于它本身吗? •什么是绝对值? •绝对值的几何意义是什么? •绝对值的代数意义是什么? •如何根据绝对值比较两个负数大小? •绝对值的应用. 小 结查看更多